Докажите что около любого треугольника можно описать окружность и только одну
Описанная окружность
Теорема
| Около любого треугольника можно описать окружность. |
Доказательство
Дано: произвольный 
Доказать: около 
Доказательство:
1. Проведем серединные перпендикуляры к сторонам 
Точка О равноудалена от вершин 

Замечание 1
| Около треугольника можно описать только одну окружность. |
Доказательство
Предположим, что около треугольника можно описать две окружности. Тогда центр каждой из них равноудален от его вершин и поэтому совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника. Следовательно, эти окружности совпадают, т.е. около треугольника можно описать только одну окружность. Что и требовалось доказать.
Замечание 2
| Около четырехугольника не всегда можно описать окружность. |
Доказательство
Рассмотрим, например, ромб, не являющийся квадратом. Такой ромб можно «поместить» в окружность так, что две его вершины будут лежать на этой окружности (Рис. 3), но нельзя «поместить» ромб в окружность так, чтобы все его вершины лежали на окружности, т.к. диаметр окружности, равный одной из диагоналей ромба, будет больше (меньше) второй диагонали, т.е. нельзя описать окружность. Что и требовалось доказать.
Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:
Доказательство
Рассмотрим четырехугольник АВСD, вписанный в окружность (Рис. 4).
Верно и обратное утверждение:
Доказательство
Доказать: около АВСD можно описать окружность.
Доказательство:
Предположим, что это не так. Тогда вершина С лежит либо внутри круга, либо вне его.
Рассмотрим первый случай, когда точка С лежит внутри круга (Рис. 6).








Рассмотрим второй случай, когда точка С лежит вне круга (Рис. 7).
Подставим (3) и (4) в (2), получим:
Примечание:
Окружность всегда можно описать:
Поделись с друзьями в социальных сетях:
Теорема: Около треугольника можно описать окружность и притом только одну и ее доказательство
Описание презентации по отдельным слайдам:
Описание слайда:
Описание слайда:
Задача
1) Нарисуйте произвольный треугольник.
2) Отметьте серединные перпендикуляры
Описание слайда:
Описание слайда:
Рассмотрим геометрическую фигуру – треугольник, с вершинами A, B, C. И центром в точке O.
A
B
C
О
Описание слайда:
Теорема:
Около треугольника можно описать окружность и притом только одну.
Описание слайда:
О чем говорится в теореме?
В теореме говорится о том, что около треугольника можно описать окружность.
A
B
C
О
Описание слайда:
Что именно говорится в теореме?
Что около любого треугольника можно описать окружность.
Описание слайда:
Что нужно доказать?
Нужно доказать, что окружность с центром в точке О, радиуса ОА, проходит через три вершины треугольника.
Как это доказать?
Нужно доказать, что точка О – центр описанной окружности и, что ОА- радиус окружности.
То есть имеем план из 2-х пунктов.
Описание слайда:
Перейдем к первому пункту плана. Как доказать, что О-центр описанной окружности?
Проведем серединные перпендикуляры к сторонам треугольника ABC.
Точка О является центром описанной окружности, (т.к. О- точка пересечения серединных перпендикуляров)
Описание слайда:
Какой из этого вывод?
О-центр описанной окружности
A
B
C
О
Описание слайда:
Первый пункт плана выполнен, теперь перейдем ко 2 пункту.
Как мы докажем, что ОА- радиус окружности?
1) проведем ОА,ОВ,ОС
2) ОА=ОВ=ОС ( т.к. точка О- равноудалена от вершин треугольника)
A
B
C
О
Описание слайда:
Какой из этого вывод?
Что ОА – радиус описанной окружности около треугольника.
A
B
C
О
Описание слайда:
Выполнив все пункты плана мы можем доказать теорему?
Да, т.к. точка О- равноудалена от вершин треугольника АВС и окружность проходит через три вершины треугольника, а значит, является описанной около треугольника АВС.
Что и требовалось доказать.
A
B
C
О
Описание слайда:
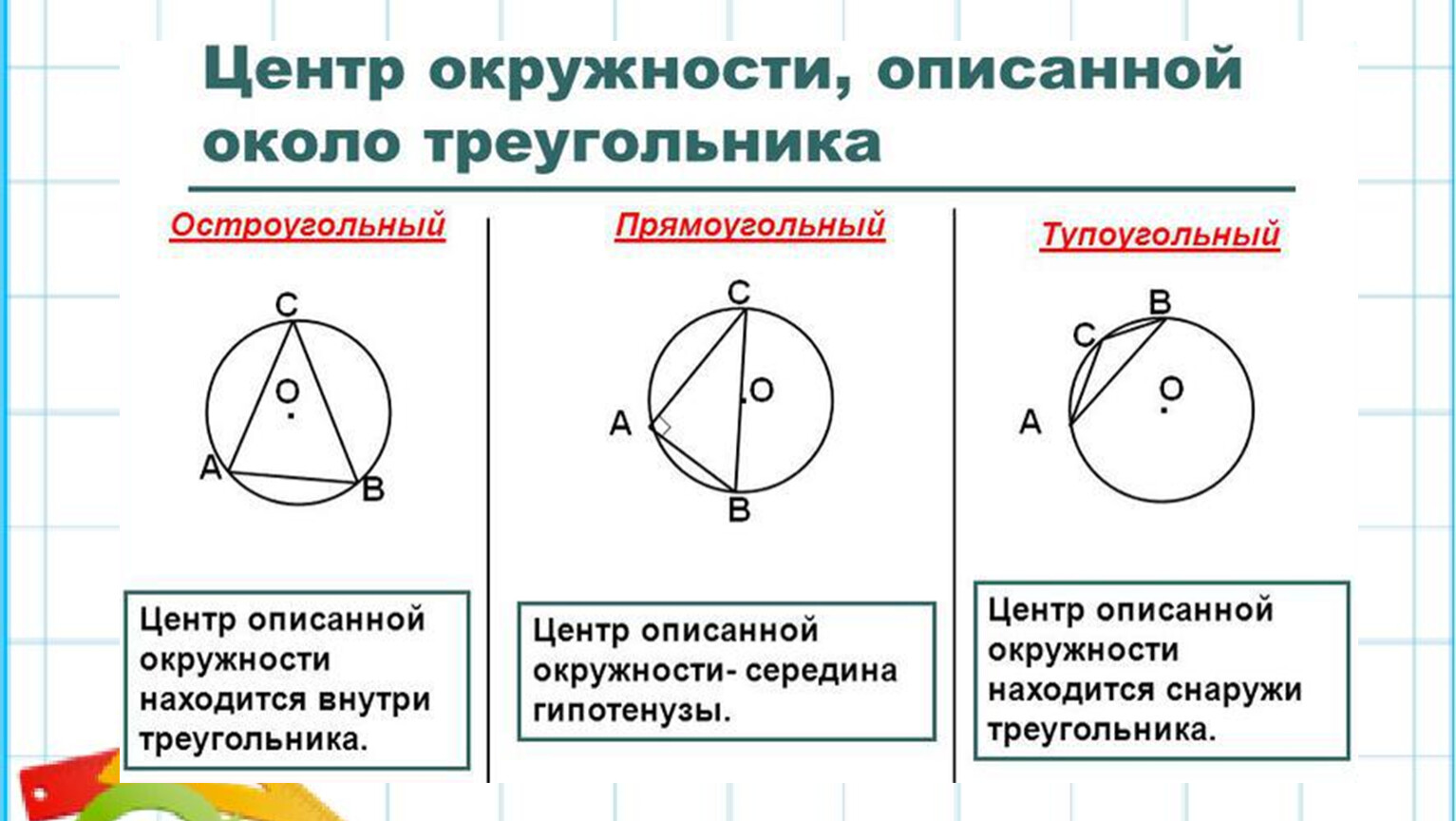
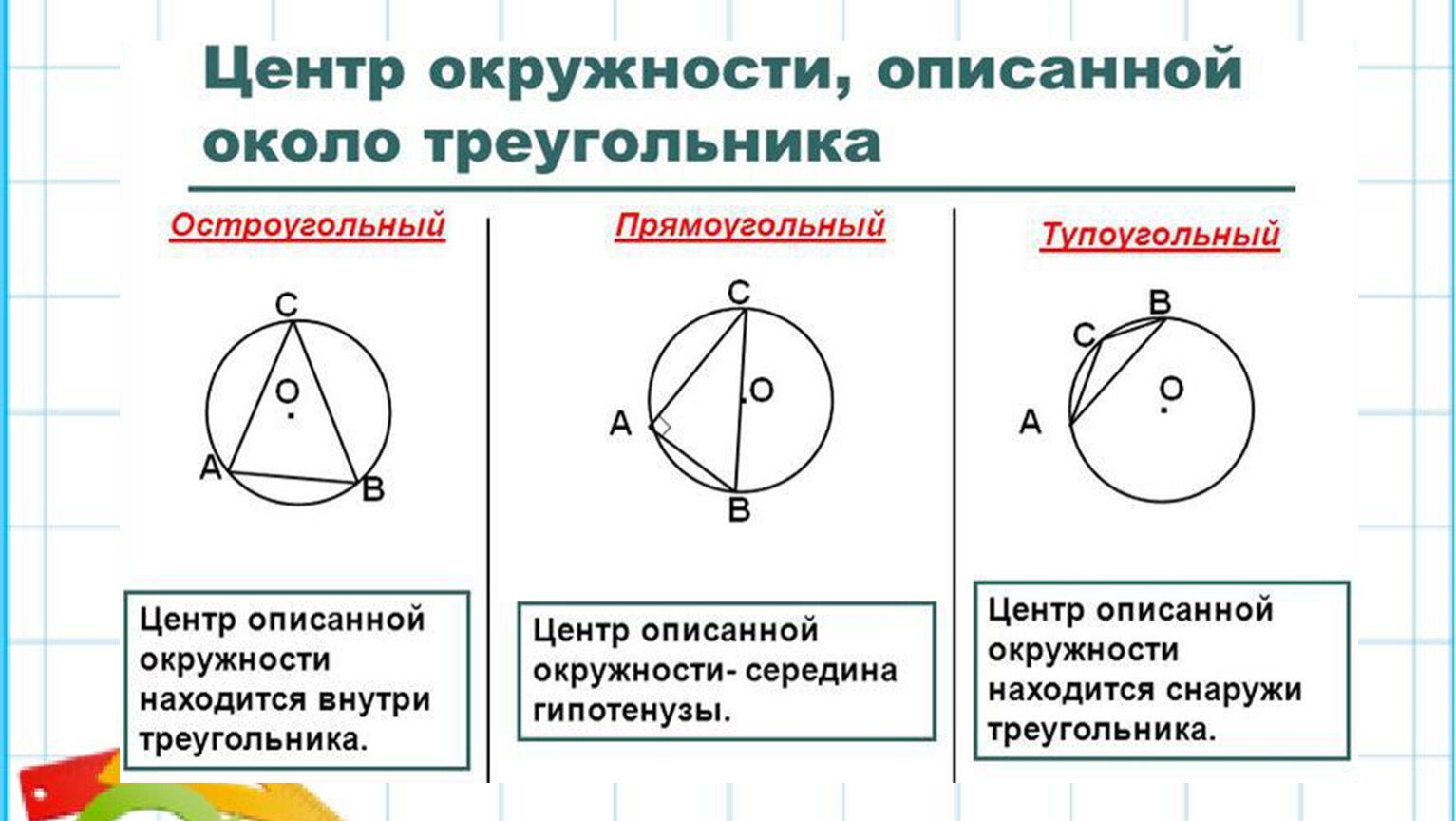
Т.к. в теореме известно,что около любого треугольника можно описать окружность и центр описанной около треугольника окружности лежит А С на пересечении серединных перпендикуляров и расположен:
а) в треугольнике, если он остроугольный;
б) на середине гипотенузы, если он прямоугольный;
в) вне треугольника, если он тупоугольный.
Описание слайда:
задача
В треугольнике даны две стороны а и в и угол С между ними. Найдите радиус описанной окружности.
Описание слайда:
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Общая информация
Похожие материалы
Презентация на тему: » Теорема о вписанном угле»
Презентация на тему: «Четыре замечательные точки треугольника. Свойство высот»
Открытый урокна тему: «Работа над ошибками контрольной работы по теме углы и расстояния в пространстве»
Презентация по геометрии на тему «Замечательные кривые своими руками»
Рабочая программа по геометрии. 7 класс
КТП Геометрия 7 класс 2 часа в неделю УМК Атанасян
ПРЕЗЕНТАЦИЯ К УРОКУ ГЕОМЕТРИИ ПО ТЕМЕ:»ТРЕУГОЛЬНИК»(7кл.)
Начальные понятия планиметрии. Геометрические фигуры.
Не нашли то что искали?
Воспользуйтесь поиском по нашей базе из
5359430 материалов.
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
Школьники из России выиграли 8 медалей на Международном турнире по информатике
Время чтения: 3 минуты
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Учителя Кубани смогут получить миллион рублей на взнос по ипотеке
Время чтения: 1 минута
В Ленобласти педагоги призеров и победителей олимпиады получат денежные поощрения
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
ДНР полностью перешла на стандарты и программы России в образовании
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Вокруг треугольника можно описать окружность
Окружность является описанной около треугольника, если все вершины треугольника лежат на этой окружности. Такой треугольник называется вписанным в окружность.
Существует теорема о том, что около каждого треугольника можно описать окружность, притом только одну. Докажем ее.
Пусть дан треугольник, к сторонам которого проведены срединные перпендикуляры. Как известно, срединные перпендикуляры треугольника всегда пересекаются в одной точке, и эта точка равноудалена от вершин треугольника. Значит, расстояние от точки пересечения срединных перпендикуляров до любой из вершин треугольника одно и то же, что может послужить радиусом одной окружности. И на этой окружности будут лежать вершины треугольника. Таким образом, она окажется описанной около него.
Чтобы убедиться в вышесказанном, рассмотрим рисунок:
Здесь дан треугольник ABC. К его сторонам проведены срединные перпендикуляры, которые пересекаются в точке O: OP ⊥ AB, OQ ⊥ BC, OR ⊥ CA.
Рассмотрим треугольники AOP и BOP. Они равны друг другу по двум равным сторонам и углу между ними: OP — общая сторона, углы при вершине P прямые, AP = BP по условию (т. к. OP срединный перпендикуляр, а значит делить AB пополам). Исходя из равенства этих треугольников, мы можем заключить, что AO = BO.
Если аналогично рассмотреть пары треугольников BOQ и COQ, COR и AOR, то можно прийти к выводу, что BO = CO, а CO = AO.
Следовательно, расстояния от точки пересечения срединных перпендикуляров треугольника до вершин этого треугольника одинаковы. Если представить, что это расстояние равно радиусу окружности с центром в точке O, то понятно, что вершины треугольника будут лежать на этой окружности.
Факт того, что около любого треугольника можно описать окружность, можно считать доказанным. Это следует из того, что к сторонам любого треугольника можно провести срединные перпендикуляры, которые всегда будут пересекаться в одной точке.
Теперь следует доказать, что описанная окружность может быть только одна. Если все вершины треугольника лежат на окружности, то это значит, что центр этой окружности находится на одинаковом расстоянии от каждой вершины треугольника. Но есть только одна точка, удаленная от вершин треугольника на одно и то же расстояние — это точка пересечения его срединных перпендикуляров. Таким образом нет других окружностей (с другими центрами и другими радиусами), которые были бы описаны вокруг треугольника.
Свойства окружности описанной около треугольника
Окружность называется описанной около многоугольника, если все его вершины лежат на этой окружности, при этом многоугольник называется вписанным в окружность (см. рис. 2).
Вся теория описанных окружностей базируется на свойстве серединного перпендикуляра (см. рис. 1). – серединный перпендикуляр.
Рис. 1. Серединный перпендикуляр
Теорема: серединный перпендикуляр является геометрическим местом точек, равноудаленных от концов отрезка. Т.е. центр окружности, описанной около отрезка, лежит на его серединном перпендикуляре.
Около многоугольника можно описать окружность тогда и только тогда, когда все его серединные перпендикуляры пересекаются в одной точке.
Рис. 2. Вписанный многоугольник
Не каждый многоугольник обладает таким свойством, любой треугольник этим свойством обладает.
Теорема 1: около любого треугольника можно описать окружность и притом только одну.
Рис. 3. Окружность, описанная вокруг треугольника
Рис. 4. Иллюстрация к доказательству
Окружность с центром в точке и радиусом описана около данного треугольника.
Мы доказали, что вокруг треугольника можно описать окружность..
Итак, мы доказали, что около любого треугольника можно описать окружность и притом только одну.
Серединные перпендикуляры и параллельны, они не имеют общих точек, иначе это был бы прямоугольник (см. рис. 5).
Рис. 5. Параллелограмм
Около прямоугольника можно описать окружность, и даже можно найти центр этой окружности.
Пусть – прямоугольник. Мы знаем, что диагонали прямоугольника равны между собой, пересекаются и точкой пересечения делятся пополам. Значит, точка равноудалена от всех вершин этого прямоугольника. является радиусом этой окружности. (см. рис. 6)
Рис. 6. Окружность, описанная около прямоугольника

Рис. 7. Окружность, описанная вокруг равнобедренной трапеции
Рис. 8. Иллюстрация к доказательству
Справедлива обратная теорема: если сумма противоположных углов выпуклого четырехугольника равна 180 градусам, то около этого четырехугольника можно описать окружность.
Рис. 9. Иллюстрация к доказательству
Рис. 10. Иллюстрация к доказательству
Противоречие, по условию, сумма противоположных углов равна 180 градусов. А значит, точка не может находиться внутри окружности.
Аналогично доказывается, что точка не может находиться вне окружности.
Задание
Докажите самостоятельно, что точка не может находиться вне окружности. При этом используйте свойство внешнего угла окружности, он измеряется полуразностью дуг, на которые опирается. Сравните ваше доказательство с доказательством, которое будет приведено ниже в разделе: «Точка вне окружности».
Итак, мы доказали, что точка не может находиться внутри окружности, не может находиться вне окружности, точка находится на окружности. Около четырехугольника можно описать окружность. Теорема доказана.
Рис. 11. Иллюстрация к задаче 1
Рис. 12. Иллюстрация к задаче 2
Мы выяснили, что такое описанная около многоугольника окружность. Установили, что около любого треугольника можно описать окружность, и притом только одну. Выяснили, что около четырехугольника можно описать окружность тогда и только тогда, когда сумма его противоположных углов равна 180 градусам.
Точка С вне окружности
Мы доказываем теорему: если сумма противоположных углов выпуклого четырехугольника равна 180 градусам, то около этого четырехугольника можно описать окружность.
Теперь докажем, что точка не может находиться вне круга (см. рис. 13).
Рис. 13. Доказательство о сумме противоположных углов вписанного выпуклого четырехугольника (точка вне круга)
Сначала вспомним свойство внешнего угла окружности: есть окружность, точка вне окружности, проведены две секущие.
Рис. 14. Свойство внешнего угла окружности
Если точка не может находиться внутри окружности и не может находиться вне окружности, значит, она находится на окружности. Что и требовалось доказать.
Список рекомендованной литературы
Домашнее задание
Треугольники, виды и свойства / math4school.ru
Подобие прямоугольных треугольников устанавливают по:
Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: В прямоугольном треугольнике гипотенуза всегда больше любого из катетов. Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе: Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе:
Следствие 2: Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Коэффициент пропорциональности равен диаметру описанной окружности:
Описанная окружность
Окружность описанная около многоугольника — это окружность, на которой лежат все вершины многоугольника.
Вписанный в окружность многоугольник — это многоугольник, все вершины которого лежат на окружности.
На рисунке 1 четырехугольник АВСD вписан в окружность с центром О, а четырехугольник АЕСD не является вписанным в эту окружность, так как вершина Е не лежит на окружности.
Теорема
| Около любого треугольника можно описать окружность. |
Доказательство
1. Проведем серединные перпендикуляры к сторонам АВС, которые пересекутся в точке О (по свойству серединных перпендикуляров треугольника). Соединим точку О с точками А, В и С (Рис. 2).
Точка О равноудалена от вершин АВС (по теореме о серединном перпендикуляре), поэтому ОА = ОВ = ОС. Следовательно, окружность с центром О радиуса ОА проходит через все три вершины треугольника, значит, является описанной около АВС. Теорема доказана.
Замечание 1
| Около треугольника можно описать только одну окружность. |
Доказательство
Предположим, что около треугольника можно описать две окружности.
Тогда центр каждой из них равноудален от его вершин и поэтому совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника.
Следовательно, эти окружности совпадают, т.е. около треугольника можно описать только одну окружность. Что и требовалось доказать.
Замечание 2
| Около четырехугольника не всегда можно описать окружность. |
Доказательство
Рассмотрим, например, ромб, не являющийся квадратом. Такой ромб можно «поместить» в окружность так, что две его вершины будут лежать на этой окружности (Рис.
3), но нельзя «поместить» ромб в окружность так, чтобы все его вершины лежали на окружности, т.к. диаметр окружности, равный одной из диагоналей ромба, будет больше (меньше) второй диагонали, т.е.
нельзя описать окружность. Что и требовалось доказать.
Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:
| В любом вписанном четырехугольнике сумма противоположных углов равна 1800. |
Доказательство
Рассмотрим четырехугольник АВСD, вписанный в окружность (Рис. 4).
Углы В и D — вписанные, тогда по теореме о вписанном угле: В = АDС, D = АВС, откуда следует В + D = АDС + АВС = (АDС + АВС). Дуги АDС и АВС вместе составляют окружность, градусная мера которой равна 3600, т.е. АDС + АВС = 3600, тогда В + D = 3600 = 1800. Что и требовалось доказать.
Верно и обратное утверждение:
| Если сумма противоположных углов четырехугольника равна 1800, то около него можно описать окружность. |
Доказательство
Проведем окружность через три вершины четырехугольника: А, В и D (Рис. 5), — и докажем, что она проходит также через вершину С, т.е.
является описанной около четырехугольника АВСD.
Предположим, что это не так. Тогда вершина С лежит либо внутри круга, либо вне его.
Рассмотрим первый случай, когда точка С лежит внутри круга (Рис. 6).
ВСD — внешний угол СFD, следовательно, BСD = ВFD + FDE. (1)
Углы ВFD и FDE — вписанные.
По теореме о вписанном угле ВFD = ВАD и FDE= ЕF, тогда, подставляя данные равенства в (1), получим: BСD = ВАD + ЕF = (ВАD + ЕF), следовательно, ВСDВАD.
BАD — вписанный, тогда по теореме о вписанном угле BАD = ВЕD, тогда BАD + BСD(ВЕD + ВАD).
Дуги ВЕD и ВАD вместе составляют окружность, градусная мера которой равна 3600, т.е. ВЕD + ВАD = 3600, тогда BАD + BСD3600 = 1800.
Итак, мы получили, что BАD + BСD1800. Но это противоречит условию BАD + BСD =1800, и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность.
Рассмотрим второй случай, когда точка С лежит вне круга (Рис. 7).
А — вписанный, тогда по теореме о вписанном угле А = ВЕD, тогда А + С(ВЕD + ВАD).
Но это противоречит условию А + С =1800, и, значит, наше предположение ошибочно, т.е.
точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность. Что и требовалось доказать.
Примечание:
Окружность всегда можно описать:
Описанная окружность — это… Что такое Описанная окружность?
Описанная окру́жность многоугольника — окружность, содержащая все вершины многоугольника. Центром является точка (принято обозначать ) пересечения серединных перпендикуляров к сторонам многоугольника.
Свойства
Для треугольника
Окружность, описанная около треугольника
Обозначаем буквой О точку пересечения серединных перпендикуляров к его сторонам и проведем отрезки ОА, ОВ и ОС. Так как точка О равноудалена от вершин треугольника АВС, то ОА = OB = ОС. Поэтому окружность с центром О радиуса ОА проходит через все три вершины треугольника и, значит, является описанной около треугольника ABC.
Радиус
Радиус описанной окружности может быть найден по формулам
Положение центра описанной окружности
Пусть радиус-векторы вершин треугольника, — радиус-вектор центра описанной окружности. Тогда
Уравнение описанной окружности
Пусть координаты вершин треугольника в некоторой декартовой системе координат на плоскости, — координаты центра описанной окружности. Тогда
Для четырехугольника
Для многоугольника
В сферическом треугольнике
Описанная окружность для сферического треугольника — это окружность, содержащая все его вершины.
См. также
Примечания
Треугольник и окружность — урок. Геометрия, 8 класс
Page 2
| 1. | Треугольники, вписанные в окружность Сложность: лёгкое |
| 2. | Треугольник, описанный около окружности Сложность: лёгкое |
| 3. | Четырёхугольник, описанный около окружности Сложность: лёгкое |
| 4. | Треугольник, вписанный в окружность Сложность: среднее |
| 5. | Диаметр окружности, который является стороной вписанного треугольника Сложность: среднее |
| 6. | Углы равнобедренного треугольника, вписанного в окружность Сложность: среднее |
| 7. | Стороны прямоугольного треугольника, вписанного в окружность, радиус окружности Сложность: среднее |
| 8. | Углы треугольника, описанного около окружности Сложность: среднее |
| 9. | Треугольник, описанный около окружности, центральные углы Сложность: среднее |
| 10. | Углы прямоугольного треугольника, описанного около окружности, центральные углы Сложность: среднее |
| 11. | Углы треугольника, описанного около окружности, даны градусные меры дуг Сложность: среднее |
| 12. | Медиана в прямоугольном треугольнике Сложность: среднее |
| 13. | Окружность, описанная и вписанная в прямоугольный треугольник Сложность: среднее |
| 14. | Окружность, описанная и вписанная в треугольник Сложность: среднее |
| 15. | Углы трапеции, вписанной в окружность Сложность: лёгкое |
| 16. | Окружность, вписанная в прямоугольную трапецию, градусные меры дуг Сложность: среднее |
| 17. | Площадь трапеции, вписанной в окружность Сложность: среднее |
| 18. | Сторона и тупой угол ромба, описанного около окружности Сложность: среднее |
| 19. | Радиус окружности, вписанной в трапецию Сложность: среднее |
| 20. | Сторона трапеции, описанной около окружности Сложность: среднее |
| 21. | Площадь трапеции, описанной около окружности Сложность: среднее |
| 22. | Окружность и равнобедренный треугольник Сложность: среднее |
| 23. | Площадь ромба, описанного около окружности Сложность: сложное |
| 24. | Радиус и площадь круга, вписанного в ромб Сложность: сложное |
| 25. | Вопросы по треугольникам и окружностям Сложность: сложное |
Page 3
Page 4
Самая удобная и увлекательная подготовка к ЕГЭ
Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник- описанным около этой окружности.
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности.
В равнобедренном треугольнике вписанная окружность точкой касания делит основание пополам
Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
В трапеции и ромбе центр вписанной окружности лежит в точке пересечения биссектрис внутренних углов, радиус вписанной окружности равен половине высоты.
В квадрате радиус вписанной окружности равен половине стороны.
1. В остроугольном треугольнике центр описанной окружности лежит внутри треугольника.
2. В тупоугольном треугольнике центр описанной окружности лежит снаружи треугольника.
3. В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы и радиус равен половине гипотенузы.
1. Угол, образованный двумя радиусами, называется центральным. Центральный угол равен градусной мере дуги, на которую он опирается
2. Угол, вершина которого лежит на окружности, а стороны являются хордами, называется вписанным. Вписанный угол равен половине градусной меры дуги, на которую он опирается
3. Угол между хордой и касательной равен половине дуги, заключенной внутри него.