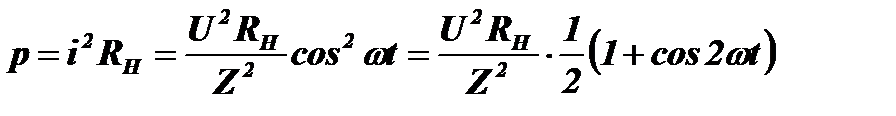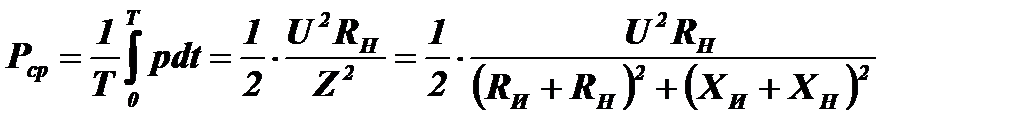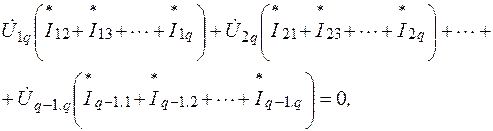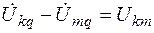Докажите что отдаваемая источником тока мощность будет максимальной при условии
Докажите что отдаваемая источником тока мощность будет максимальной при условии
ЛАБОРАТОРНАЯ РАБОТА № 3.7.
ИССЛЕДОВАНИЕ ПОЛЕЗНОЙ МОЩНОСТИ И КПД ИСТОЧНИКОВ ТОКА
Фамилия И.О. _____________ Группа ______ Дата ______
Цель данной работы – экспериментально проверить теоретические выводы о зависимости полезной мощности и КПД источника тока от сопротивления нагрузки.
Электрическая цепь состоит из источника тока, подводящих проводов и нагрузки или потребителя тока. Каждый из этих элементов цепи обладает сопротивлением.
Сопротивление подводящих проводов обычно бывает очень мало, поэтому им можно пренебречь. В каждом участке цепи будет расходоваться энергия источника тока. Весьма важное практическое значение имеет вопрос о целесообразном расходовании электрической энергии.
Полная мощность Р, выделяемая в цепи, будет слагаться из мощностей, выделяемых во внешней и внутренней частях цепи: P = I 2 ·R + I 2 ·r = I 2 (R + r). Так как I(R + r) = ε, то Р =I·ε,
где R – внешнее сопротивление; r – внутреннее сопротивление; ε – ЭДС источника тока.
Таким образом, полная мощность, выделяемая в цепи, выражается произведением силы тока на ЭДС элемента. Эта мощность выделяется за счет каких-либо сторонних источников энергии; такими источниками энергии могут быть, например, химические процессы, происходящие в элементе.
Рассмотрим, как зависит мощность, выделяемая в цепи, от внешнего сопротивления R, на которое замкнут элемент. Предположим, что элемент данной ЭДС и данного внутреннего сопротивления r замыкается внешним сопротивлением R; определим зависимость от R полной мощности Р, выделяемой в цепи, мощности Ра, выделяемой во внешней части цепи и КПД.
Сила тока I в цепи выражается по закону Ома соотношением
Полная мощность, выделяемая в цепи, будет равна
При увеличении R мощность падает, стремясь асимптотически к нулю при неограниченном увеличении R.
Мощность, выделяющаяся во внешней части цепи, равна
Отсюда видно, что полезная мощность Ра равна нулю в двух случаях – при R = 0 и R = ∞.
Исследуя функцию Ра = f(R) на экстремум, получим, что Ра достигает максимума при R = r, тогда
Чтобы убедится в том, что максимум мощности Ра получается при R = r, возьмем производную Ра по внешнему сопротивлению
По условию максимума требуется равенство нулю первой производной



Можно убедиться, что при этом условии мы получим максимум, а не минимум для Ра, определив знак второй производной 
Коэффициент полезного действия (КПД) η источника ЭДС это величина отношения мощности Ра, выделяющейся во внешней цепи, к полной мощности Р, развиваемой источником ЭДС.
В сущности КПД источника ЭДС указывает, какая доля работы сторонних сил преобразуется в электрическую энергию и отдается во внешнюю цепь.
Выражая мощность через силу тока I, разность потенциалов во внешней цепи U и величину электродвижущей силы ε, получим
То есть КПД источника ЭДС равен отношению напряжения во внешней цепи к ЭДС. В условиях применимости закона Ома можно далее заменить U = IR; ε = I(R + r), тогда
Следовательно, в том случае, когда вся энергия расходуется на Ленц-Джоулево тепло, КПД источника ЭДС равен отношению внешнего сопротивления к полному сопротивлению цепи.
При R = 0 имеем η = 0. С увеличением R, КПД возрастает, стремится к значению η=1 при неограниченном увеличении R, однако при этом мощность, выделяющаяся во внешней цепи, стремится к нулю. Таким образом, требования одновременного получения максимальной полезной мощности при максимальном КПД невыполнимы.
Когда Ра достигает максимума, то η = 50%. Когда же КПД η близок к единице, полезная мощность мала по сравнению с максимальной мощностью, которую мог бы развивать данный источник. Поэтому для увеличения КПД необходимо по возможности уменьшать внутреннее сопротивление источника ЭДС, например, аккумулятора или динамо-машины.
В случае R = 0 (короткое замыкание) Ра = 0 и вся мощность выделяется внутри источника. Это может привести к перегреву внутренних частей источника и выводу его из строя. По этой причине короткие замыкания источников (динамо-машины, аккумуляторные батареи) недопустимы!
На рис. 1 кривая 1 дает зависимость мощности Ра, выделяемой во внешней цепи, от сопротивления внешней части цепи R; кривая 2 дает зависимость от R полной мощности Р; кривая 3 – ход КПД η от того же внешнего сопротивления.
Порядок выполнения работы
1. Ознакомиться со схемой на стенде.
2. Установить с помощью магазина сопротивление R = 100 Ом.
4. Произвести измерения силы тока в цепи последовательно для различных девяти сопротивлений на магазине сопротивлений, начиная от 100 Ом и выше. Внести в таблицу результаты измерений силы тока, выразив их в амперах.
5. Выключить ключ К.
6. Вычислить для каждого сопротивления Р, Ра (в ваттах) и η.
7. Построить графики Р, Ра и η от R.
1. Что называется КПД источника ЭДС?
2. Вывести формулу КПД источника ЭДС.
3. Что такое полезная мощность источника ЭДС?
4. Вывести формулу полезной мощности источника ЭДС.
5. Чему равна максимальная мощность, выделяемая во внешней цепи (Ра)max?
6. При каком значении R полная мощность Р, выделяющаяся в цепи, максимальна?
7. Чему равен КПД источника ЭДС при (Ра)max?
8. Произвести исследование функции (Ра) = f(R) на экстремум.
9. Зарисовать график зависимости Р, Ра и η от внешнего сопротивления R.
10. Что такое ЭДС источника?
11. Почему сторонние силы должны быть не электрического происхождения?
12. Почему недопустимо короткое замыкание для источников напряжения?


Условия передачи максимальной мощности от источника энергии к нагрузке.
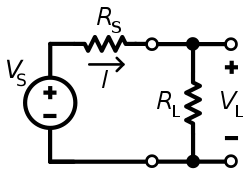
Практически во всех энергетических и информационных системах происходит передача электрической энергии в той или иной ее форме от некоторого источника к некоторой нагрузке. Как правило, в нагрузку необходимо передать максимально возможную часть мощности источника. В большинстве случаев вообще желательно передать в нагрузку всю мощность, имеющуюся в источнике. Так, например, очевидно, что нет необходимости сохранять какую-либо часть мощности в электростанции. Лучше её всю передать потребителям электроэнергии. Нет необходимости оставлять сколько-нибудь мощности в передатчике радиостанции. Для увеличения дальности и повышения качества связи желательно направить всю его мощность в антенну. Образно говоря, мы хотели бы передать всю мощность из источника в нагрузку, также как мы переливаем жидкость из одного сосуда в другой.
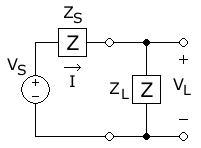
Рассмотрим простую электрическую схему, изображённую на рис. 6.2. Это цепь постоянного тока. Общее сопротивление цепи равно R=RИ+RН. Ток в цепи: I=U/R. Мощность, выделяемая в нагрузке, будет равна:
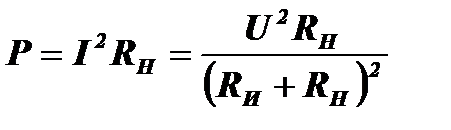
Чтобы найти максимум этой мощности, необходимо найти производную 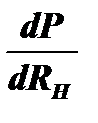
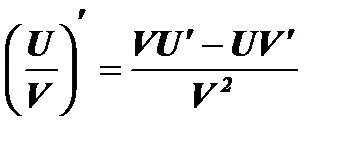
Отсюда: 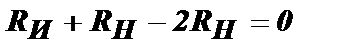
При соблюдении этого условия в нагрузку отдаётся мощность
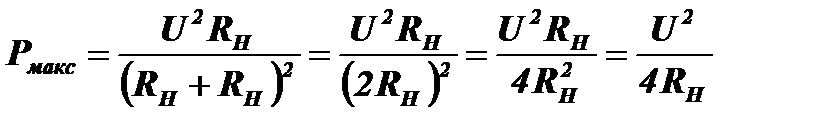
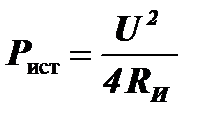
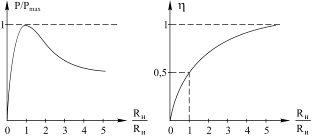
| а) б) Рис. 6.3 Зависимость мощности, выделяемой в нагрузке (а) и КПД системы (б) от отношения сопротивления нагрузки к внутреннему сопротивлению источника |
КПД системы передачи мощности от источника в нагрузку при этом составляет 0,5, поскольку половина мощности выделяется на сопротивлении источника. Таким образом, в наилучшем случае только половина мощности попадёт из источника в нагрузку. Во всех иных случаях доля этой мощности будет ещё меньше. На рисунке 6.3 показана зависимость относительной мощности, передаваемой в нагрузку P/Pmax и КПД системы η от соотношения RН/RИ.
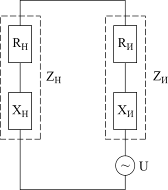
Теперь рассмотрим источник переменного тока, который развивает на произвольной частоте ω напряжение u=Ucosωt и в общем случае имеет комплексное внутреннее сопротивление ZИ=RИ+XИ, где RИ и XИ соответственно активная и реактивная части его внутреннего сопротивления. Сопротивление нагрузки также состоит из активной и реактивной частей ZН=RН+XН (рис.6.4).
| Рис. 6.4 Схема цепи переменного тока |
Общая активная нагрузка, на которую работает источник, будет равна (RИ+RН), а общая реактивная часть этой нагрузки будет равна (XИ+XН). Полное сопротивление этой смешанной активно-реактивной цепи определяется по формуле: 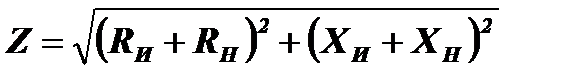
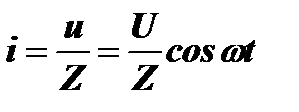
Средняя мощность за период:
Сначала определим роль реактивных сопротивлений в получении максимума этой мощности. Очевидно, что при любых значениях RИ и RН активная мощность достигнет наибольшей величины при условии (XИ+XН)=0, т.е. при взаимной компенсации реактивных сопротивлений источника и нагрузки XИ=−XН.
Аналогичная картина возникает в обычном колебательном контуре при резонансе. Когда реактивное сопротивление емкости контура становится равным, но противоположным по знаку реактивному сопротивлению индуктивности, в последовательном контуре создаются условия для получения максимального тока.
При XИ=−XН средняя мощность за период будет равна: 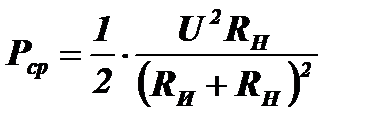
Таким образом, для получения максимальной мощности в нагрузке, активные сопротивления источника и нагрузки должны быть равны, а их реактивные сопротивления должны быть равны по абсолютной величине, но иметь противоположные знаки. Для взаимной компенсации напряжения на реактивных сопротивлениях источника и нагрузки должны быть сдвинуты по фазе на 90 0 в разные стороны относительно тока в цепи. Эти напряжения являются, как бы, зеркальным отображением друг друга.
Если представить сопротивления источника и нагрузки в виде комплексных чисел, то нетрудно заметить, что для передачи максимальной мощности от источника в нагрузку сопротивления источника энергии и потребителя энергии должны быть комплексно сопряжёнными ZИ=RИ+iXИ и ZН=RН−iXН.
Следует отметить, что согласование нагрузки и источника является очень широким понятием и проявляется в самых разных областях.
Возьмем более близкий нам пример: электрическая батарея нагревает электрическую плиту. Каким должно быть сопротивление плиты, чтобы она отбирала от батареи максимум мощности? Количество тепла, выделяемого электроплитой, пропорционально току в цепи. Если сделать сопротивление плиты значительно больше, чем сопротивление батареи, то ток в цепи будет мал и тепла в электроплите выделится очень мало. Если сопротивление плиты сделать значительно меньше, чем сопротивление батареи, то ток в цепи станет большим, но тепло будет выделяться, в основном, в электрической батарее, а не в плите. В обоих случаях электроплита дает мало тепла. Наибольшее количество тепла будет выделяться в электроплите, когда сопротивления плиты и батареи будут равны. В этом случае и в батарее и в плите будет выделяться одинаковое количество тепла, равное только 50% от общей мощности батареи.
Для согласования сопротивлений источника и нагрузки существует много способов. В механике для передачи максимума мощности используется рычаг. Расширяющийся раструб рупорной антенны согласовывает волновод со свободным пространством. Врач использует стетоскоп, чтобы согласовать акустические сопротивления своего уха и грудной клетки пациента. Сердце человека также согласовано по сопротивлению с системой артерий и вен, хотя это согласование с возрастом ухудшается.
УСЛОВИЕ ПЕРЕДАЧИ ИСТОЧНИКОМ МАКСИМУМА МОЩНОСТИ ПРИ ЗАДАННОМ КОЭФФИЦИЕНТЕ МОЩНОСТИ ПРИЕМНИКА
На практике часто возникает необходимость подбора комплексного сопротивления нагрузки таким образом, чтобы при заданных комплексном сопротивлении источника и коэффициенте мощности приемника обеспечивалась передача максимума полной и соответственно средней мощности от источника приемнику.
Пользуясь условными обозначениями, принятыми в предыдущем параграфе, находим полную мощность на зажимах нагрузки:
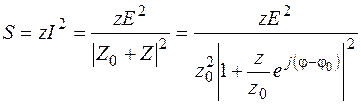
После преобразования получим:
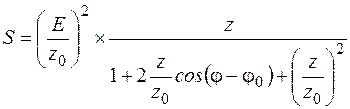
Приняв величину z за переменную, записываем условие максимума функции S
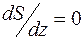
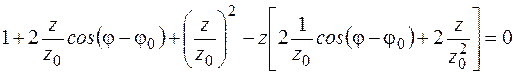
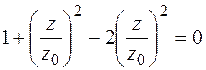
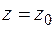
Подстановка (3.19) в (3.18) дает
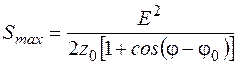
Если условие (3.19) не соблюдается, то относительное отклонение передаваемой полной мощности от максимальной составляет
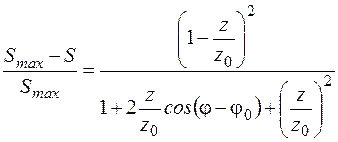
Практически допустимы отклонения от условия (3.19), при которых величина (3.20) не превышает заданного предела.
Условия передачи максимума мощности широко используются в радиотехнике, электропроводной связи, автоматике и приборостроении. В энергетических же системах, генерирующих и потребляющих большие мощности, стремятся обеспечить высокий к.п.д. генераторов; поэтому сопротивления нагрузок значительно превышают сопротивления генераторов.
БАЛАНС МОЩНОСТЕЙ
Из закона сохранения энергии следует, что для любой электрической цепи соблюдается закон баланса активных мощностей: активная мощность, генерируемая источниками, равна активной мощности, потребляемой всеми приемниками.
В свою очередь можно показать, что сумма отдаваемых реактивных мощностей равна сумме потребляемых реактивных мощностей.
Если воспользоваться комплексной формой записи токов, напряжений и мощностей, то высказанные положения будут вытекать из следующих рассуждений.
Для электрической цепи, содержащей q узлов, можно написать по первому закону Кирхгофа q – 1 уравнений вида
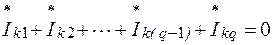
где положительные направления всех токов приняты от узла k к узлам 1, 2. q.
Умножим каждое из этих уравнений на комплексное напряжение, отсчитываемое от соответствующего узла к узлу q, и просуммируем эти произведения
откуда с учетом того, что
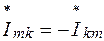
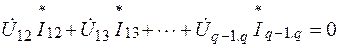
Итак, сумма комплексных мощностей, потребляемых всеми ветвями электрической цепи, равна нулю; следовательно, также равны нулю в отдельности алгебраические суммы действительных и мнимых частей мощностей.
Иначе говоря, равна нулю как алгебраическая сумма потребляемых всеми ветвями цепи средних мощностей, так и алгебраическая сумма потребляемых реактивных мощностей.
Поскольку отрицательные потребляемые мощности представляют собой мощности отдаваемые, то отсюда следует закон баланса как средних, так и реактивных мощностей.
В случае цепи постоянного тока сумма мощностей источников равна сумме мощностей, расходуемых в сопротивлениях, причем знаки мощностей источников определяются по указанному выше правилу:
мощность положительна при совпадении направлений ЭДС E и тока I, проходящего через источник, и отрицательна при встречном направлении ЭДС и тока. В последнем случае, если источником энергии служит аккумулятор, то мощность EI расходуется на его зарядку; если же источником служит генератор, то мощность EI расходуется на механическую работу (генератор работает в режиме двигателя).
Дата добавления: 2015-12-16 ; просмотров: 794 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Исследование зависимости мощности и КПД источника тока от внешней нагрузки
ЗАКОН ОМА ДЛЯ ПОЛНОЙ ЦЕПИ:
I- сила тока в цепи; Е- электродвижущая сила источника тока, включённого в цепь; R- сопротивление внешней цепи; r- внутреннее сопротивление источника тока.
МОЩНОСТЬ, ВЫДЕЛЯЕМАЯ ВО ВНЕШНЕЙ ЦЕПИ
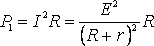
Из формулы (2) видно, что при коротком замыкании цепи (R®0) и при R®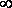
Следовательно, мощность, выделяемая во внешней цепи, достигает наибольшего значения при сопротивлении внешней цепи равном внутреннему сопротивлению источника тока.
При этом сила тока в цепи 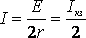
равна половине тока короткого замыкания. При этом мощность, выделяемая во внешней цепи, достигает своего максимального значения, равного
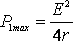
Когда источник замкнут на внешнее сопротивление, то ток протекает и внутри источника и при этом на внутреннем сопротивлении источника выделяется некоторое количество тепла. Мощность, затрачиваемая на выделение этого тепла равна
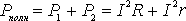
КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ
КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ источника тока равен 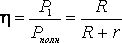
Из формулы (8) следует, что
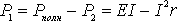
т.е. Р1 изменяется с изменением силы тока в цепи по параболическому закону и принимает нулевые значения при I = 0 и при 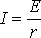
Если сопротивление нагрузки меньше, чем сопротивление источника, то большая часть мощности в конечном итоге рассеивается в источнике, и хотя общая рассеиваемая мощность выше из-за более низкого общего сопротивления, оказывается, что количество рассеиваемой в нагрузке уменьшен.
Недавние пояснительные статьи иллюстрируют, как фундаментальная математика теоремы о максимальной мощности также применима к другим физическим ситуациям, таким как:
СОДЕРЖАНИЕ
Максимизация передачи мощности по сравнению с энергоэффективностью
Первоначально теорема была неправильно истолкована (особенно Джоулем ) как предполагающая, что система, состоящая из электродвигателя, приводимого в действие батареей, не может иметь КПД более 50%, поскольку, когда импедансы совпадают, мощность, теряемая в виде тепла в батарее, всегда будет быть равным мощности, подаваемой на двигатель.
Рассмотрим три частных случая:
КПД составляет всего 50%, когда достигается максимальная передача мощности, но приближается к 100%, когда сопротивление нагрузки приближается к бесконечности, хотя общий уровень мощности стремится к нулю.
КПД также приближается к 100%, если сопротивление источника приближается к нулю, и к 0%, если сопротивление нагрузки приближается к нулю. В последнем случае вся мощность потребляется внутри источника (если источник также не имеет сопротивления), поэтому мощность, рассеиваемая при коротком замыкании, равна нулю.
Согласование импеданса
Расчетное доказательство для чисто резистивных цепей
Мощность P L, рассеиваемая в нагрузке, равна квадрату силы тока, умноженного на сопротивление:
Значение R L, для которого это выражение является максимальным, можно вычислить путем дифференцирования, но легче вычислить значение R L, для которого знаменатель
р S 2 / р L + 2 р S + р L <\ Displaystyle R _ <\ mathrm > ^ <2>/ R _ <\ mathrm > + R _ <\ mathrm
это минимум. В любом случае результат будет одинаковым. Дифференцируя знаменатель по R L :
Для максимума или минимума первая производная равна нулю, поэтому
р S 2 / р L 2 знак равно 1 <\ Displaystyle R _ <\ mathrm > ^ <2>/ R _ <\ mathrm
В практических резистивных схемах R S и R L оба положительные, поэтому положительный знак в приведенном выше является правильным решением.
Чтобы узнать, является ли это решение минимумом или максимумом, выражение знаменателя снова дифференцируется:
\ Omega> 
\ Omega> 
> \, \!> 
\ Omega>
Обратите внимание, что это показывает, что максимальная передача мощности также может быть интерпретирована как напряжение нагрузки, равное половине эквивалента напряжения Тевенина источника.
В реактивных цепях
Теорема о передаче мощности также применима, когда источник и / или нагрузка не являются чисто резистивными.
Уточнение теоремы о максимальной мощности гласит, что любые реактивные компоненты источника и нагрузки должны быть одинаковой величины, но противоположного знака. ( См. Вывод ниже. )
Физически реализуемые источники и нагрузки обычно не являются чисто резистивными, имеют некоторые индуктивные или емкостные компоненты, и поэтому практические применения этой теоремы под названием комплексно сопряженного согласования импедансов фактически существуют.
Если источник является полностью индуктивным (емкостным), то полностью емкостная (индуктивная) нагрузка при отсутствии резистивных потерь будет получать 100% энергии от источника, но отправлять ее обратно через четверть цикла.
Коррекция коэффициента мощности (где индуктивное реактивное сопротивление используется для «уравновешивания» емкостного), по сути, является той же идеей, что и согласование комплексно-сопряженного импеданса, хотя это делается по совершенно другим причинам.
Для фиксированного реактивного источника теорема максимальной мощности максимизирует активную мощность (P), подаваемую на нагрузку, путем комплексно-сопряженного согласования нагрузки с источником.
Для фиксированной реактивной нагрузки коррекция коэффициента мощности сводит к минимуму полную мощность (S) (и ненужный ток), проводимую линиями передачи, при сохранении той же величины передаваемой активной мощности.
Это делается путем добавления реактивного сопротивления к нагрузке, чтобы сбалансировать собственное реактивное сопротивление нагрузки, изменяя сопротивление реактивной нагрузки на сопротивление резистивной нагрузки.
Доказательство
Средняя мощность, рассеиваемая в нагрузке, равна квадрату тока, умноженного на резистивную часть (действительную часть) импеданса нагрузки : п L <\ displaystyle P _ <\ text 

( р S + р L ) 2 + ( Икс S + Икс L ) 2 <\ displaystyle (R _ <\ text > + R _ <\ text > + X _ <\ text
это минимум. Поскольку реактивные сопротивления могут быть отрицательными, это достигается путем адаптации реактивного сопротивления нагрузки к
Это сокращает приведенное выше уравнение до:
п L знак равно 1 2 | V S | 2 р L ( р S + р L ) 2 <\ displaystyle P _ <\ text > | ^ <2>R _ <\ text > + R _ <\ text
Два условия максимизации