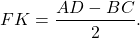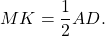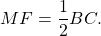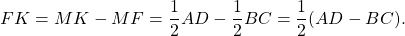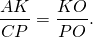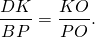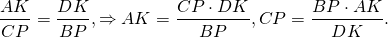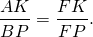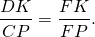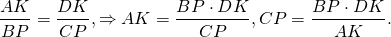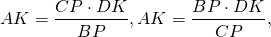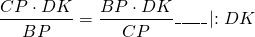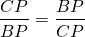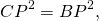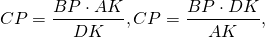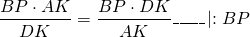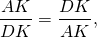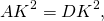Докажите что отрезок соединяющий середины оснований трапеции параллелен основаниям трапеции

Докажите что отрезок соединяющий середины оснований трапеции параллелен основаниям трапеции

Докажите, что отрезок, соединяющий середины оснований трапеции, делит её на две равные по площади части.

Пусть ABCD — трапеция, M и N — середины оснований AD и BC соответвенно.

Пусть AM = MD = a и BN = NC = b, а h — высота трапеции. Тогда площадь каждой из частей, на которые отрезок MN делит трапецию, равна то есть, эти части равновелики.

Приведем другое решение.

Пусть — длина высоты трапеции. Площадь треугольника равна площади треугольника поскольку высоты, проведённые к основаниям и равны, а основания и равны. Аналогично равны площади треугольников и Покажем, что площади четырёхугольников и равны:

Источник

Отрезок, соединяющий середины диагоналей трапеции

Свойства отрезка, соединяющего середины диагоналей трапеции

Отрезок, соединяющий середины диагоналей трапеции

1) лежит на средней линии трапеции,

2) равен полуразности оснований трапеции.

Дано: ABCD — трапеция, AD||BC,

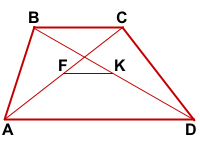
F — середина AC, K — середина BD,

MN — средняя линия трапеции

Так MN — средняя линия трапеции ABCD, то M — середина AB, N — середина CD, и MN||AD, MN||BC.

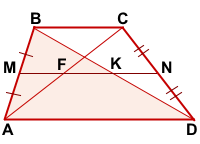
Рассмотрим угол ABD.

Так как AM=BM и MN||AD, то по теореме Фалеса, отрезки, на которые прямая MN делит BD, также равны, то есть MN пересекает отрезок BD в его середине, то есть в точке K.

Аналогично, для угла BAC:

AM=BM, MN||AD, следовательно, по теореме Фалеса прямая MN пересекает отрезок AC в его середине, то есть в точке F.

Таким образом, отрезок, соединяющий середины диагонали трапеции, параллелен основаниям трапеции и лежит на её средней линии.

MF — средняя линия треугольника ABC. Поэтому

Что и требовалось доказать.

Если использовать обозначения AD=a, BC=b, то формула длины отрезка, соединяющего середины диагоналей трапеции, примет вид

Источник

Замечательное свойство трапеции

Замечательное свойство трапеции

Точка пересечения диагоналей трапеции, точка пересечения продолжения боковых сторон трапеции и середины оснований трапеции лежат на одной прямой.

Существует несколько способов доказательства этого свойства. Надо доказать, что четыре данные точки лежат на одной прямой. Прямую можно провести через любые две точки. Выбирают две любые точки из четырёх, проводят через них прямую и доказывают, что две другие точки также лежат на этой прямой.

Сформулируем это свойство иначе:

Прямая, проходящая через точку пересечения диагоналей трапеции и точку пересечения продолжения её боковых сторон, делит основания трапеции пополам.

Дано:

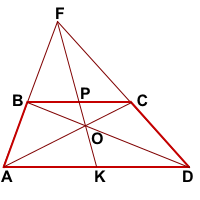
ABCD- трапеция, AD||BC,

Доказать: K- середина AD,

Рассмотрим треугольники AOK и COP.

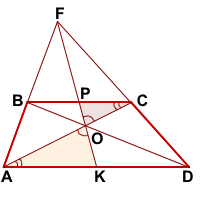
∠OAK=∠OCP (как внутренние накрест лежащие при AD||BC и секущей AC).

Значит, треугольники AOK и COP подобны (по двум углам).

Аналогично, треугольники DOK и BOP подобны и

Так как правые части этих равенств равны, то левые также равны:

Рассмотрим треугольники AFK и BFP.

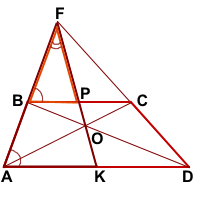
∠KAF=∠PBF (как соответственные при AD||BC и секущей AF).

Следовательно, треугольники AFK и BFP подобны (по двум углам).

Аналогично, треугольники DFK и CFP подобны и

Правые части равенств равны, приравниваем левые части:

а значит, CP=BP, то есть P — середина BC.

AK=DK, K — середина AD.

Что и требовалось доказать.

В нашем случае докажем, что точки O и P лежат на прямой FK.

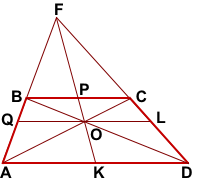
FK — медиана треугольника AFD.

Проведём через точку O пересечения диагоналей трапеции отрезок QL с концами на боковых сторонах трапеции.

BC||AD (как основания трапеции), QL||AD (по построению).

Так как медиана, проведённая к стороне треугольника, делит пополам любой отрезок, параллельный этой стороне, с концами на двух других сторонах треугольника, то точки P и O лежат прямой FK.

Поскольку медиана FK, проведённая к AD, делит пополам любой отрезок, параллельный AD, с концами на сторонах AF и DF, то среднюю линию трапеции она также делит пополам. Таким образом, замечательное свойство трапеции можно дополнить:

Точка пересечения диагоналей трапеции, точка пересечения продолжения боковых сторон трапеции, середины оснований трапеции и середина средней линии трапеции лежат на одной прямой.

Источник

Докажите что отрезок соединяющий середины оснований трапеции параллелен основаниям трапеции

Задание 16. Отрезок, соединяющий середины М и N оснований соответственно ВС и AD трапеции ABCD, разбивает её на две трапеции, в каждую из которых можно вписать окружность.

а) Докажите, что трапеция ABCD равнобедренная.

б) Известно, что радиус этих окружностей равен 4, а меньшее основание ВС исходной трапеции равно 14. Найдите радиус окружности, касающейся боковой стороны АВ, основания AN трапеции ABMN и вписанной в неё окружности.

а) Дана трапеция ABCD, в которой M – середина BC, а N – середина AD (см. рисунок ниже). Следовательно,

По условию задания в трапецию ABMN можно вписать окружность, значит, суммы ее противоположных сторон равны:

Аналогично для трапеции MCDN:

Приравниваем два выражения для MN, имеем:

и, учитывая равенство (1), получаем:

Получаем равенство боковых сторон, значит, трапеция ABCD – равнобедренная.

б) Так как радиус вписанных окружностей равен 4, значит, высота трапеции MN=2∙4=8. Также по условию дана длина BC=14 и, следовательно, BM=BC:2=14:2=7. Обозначим BF через x (см. рисунок ниже). Тогда BM1=x как отрезки касательных.

Получаем, что M1M=7-x, поэтому и MZ=7-x,

следовательно, N1N=x+1 (так как соответствующие отрезки касательных равны). Так как MZ=ZN (радиус O1Z вписанной окружности будет параллелен основаниям трапеции), имеем:

Значит, BF=BM1 = 3. Рассмотрим прямоугольный треугольник BO1A (он прямоугольный, так как AO1 и BO1 – биссектрисы, а , поэтому ). Квадрат высоты OF1, проведенной из прямого угла, равен:

и по теореме Пифагора

Обозначим радиус малой окружности AO=y, тогда

Учитывая, что треугольники AFO1 и AYO подобны по двум углам, можем записать отношение:

Источник