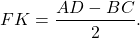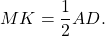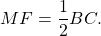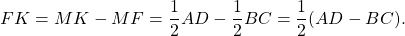Докажите что отрезок соединяющий середины

Докажите что отрезок соединяющий середины

Докажите, что отрезок, соединяющий середины оснований трапеции, делит её на две равные по площади части.

Пусть ABCD — трапеция, M и N — середины оснований AD и BC соответвенно.

Пусть AM = MD = a и BN = NC = b, а h — высота трапеции. Тогда площадь каждой из частей, на которые отрезок MN делит трапецию, равна то есть, эти части равновелики.

Приведем другое решение.

Пусть — длина высоты трапеции. Площадь треугольника равна площади треугольника поскольку высоты, проведённые к основаниям и равны, а основания и равны. Аналогично равны площади треугольников и Покажем, что площади четырёхугольников и равны:

Источник

Отрезок, соединяющий середины диагоналей трапеции

Свойства отрезка, соединяющего середины диагоналей трапеции

Отрезок, соединяющий середины диагоналей трапеции

1) лежит на средней линии трапеции,

2) равен полуразности оснований трапеции.

Дано: ABCD — трапеция, AD||BC,

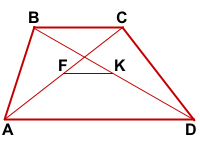
F — середина AC, K — середина BD,

MN — средняя линия трапеции

Так MN — средняя линия трапеции ABCD, то M — середина AB, N — середина CD, и MN||AD, MN||BC.

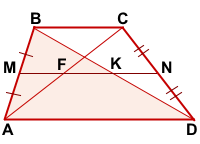
Рассмотрим угол ABD.

Так как AM=BM и MN||AD, то по теореме Фалеса, отрезки, на которые прямая MN делит BD, также равны, то есть MN пересекает отрезок BD в его середине, то есть в точке K.

Аналогично, для угла BAC:

AM=BM, MN||AD, следовательно, по теореме Фалеса прямая MN пересекает отрезок AC в его середине, то есть в точке F.

Таким образом, отрезок, соединяющий середины диагонали трапеции, параллелен основаниям трапеции и лежит на её средней линии.

MF — средняя линия треугольника ABC. Поэтому

Что и требовалось доказать.

Если использовать обозначения AD=a, BC=b, то формула длины отрезка, соединяющего середины диагоналей трапеции, примет вид

Источник

Докажите что отрезок соединяющий середины

Задание 16. Отрезок, соединяющий середины М и N оснований соответственно ВС и AD трапеции ABCD, разбивает её на две трапеции, в каждую из которых можно вписать окружность.

а) Докажите, что трапеция ABCD равнобедренная.

б) Известно, что радиус этих окружностей равен 4, а меньшее основание ВС исходной трапеции равно 14. Найдите радиус окружности, касающейся боковой стороны АВ, основания AN трапеции ABMN и вписанной в неё окружности.

а) Дана трапеция ABCD, в которой M – середина BC, а N – середина AD (см. рисунок ниже). Следовательно,

По условию задания в трапецию ABMN можно вписать окружность, значит, суммы ее противоположных сторон равны:

Аналогично для трапеции MCDN:

Приравниваем два выражения для MN, имеем:

и, учитывая равенство (1), получаем:

Получаем равенство боковых сторон, значит, трапеция ABCD – равнобедренная.

б) Так как радиус вписанных окружностей равен 4, значит, высота трапеции MN=2∙4=8. Также по условию дана длина BC=14 и, следовательно, BM=BC:2=14:2=7. Обозначим BF через x (см. рисунок ниже). Тогда BM1=x как отрезки касательных.

Получаем, что M1M=7-x, поэтому и MZ=7-x,

следовательно, N1N=x+1 (так как соответствующие отрезки касательных равны). Так как MZ=ZN (радиус O1Z вписанной окружности будет параллелен основаниям трапеции), имеем:

Значит, BF=BM1 = 3. Рассмотрим прямоугольный треугольник BO1A (он прямоугольный, так как AO1 и BO1 – биссектрисы, а , поэтому ). Квадрат высоты OF1, проведенной из прямого угла, равен:

и по теореме Пифагора

Обозначим радиус малой окружности AO=y, тогда

Учитывая, что треугольники AFO1 и AYO подобны по двум углам, можем записать отношение:

Источник