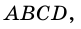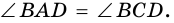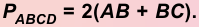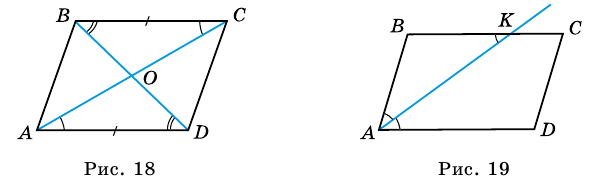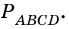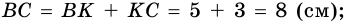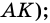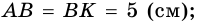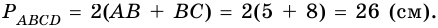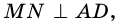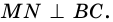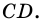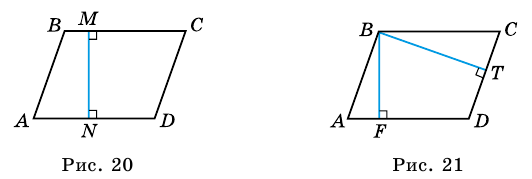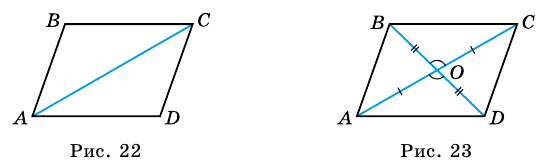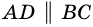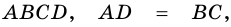Докажите что параллелограмм является выпуклым четырехугольником номер 378

Параллелограмм, его свойства и признаки с примерами решения

Параллелограммом называют четырехугольник, у которого противолежащие стороны попарно параллельны.

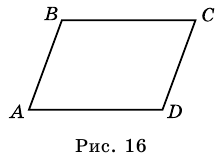
На рисунке 16 изображен параллелограмм

Рассмотрим свойства параллелограмма.

1. Сумма двух любых соседних углов параллелограмма равна 180°.

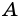
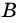
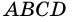
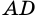
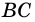
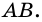
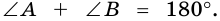
Действительно, углы и параллелограмма (рис. 16) являются внутренними односторонними углами для параллельных прямых и и секущей Поэтому Аналогично это свойство можно доказать для любой другой пары соседних углов параллелограмма.

2. Параллелограмм является выпуклым четырехугольником.

3. В параллелограмме противолежащие стороны равны и противолежащие углы равны.

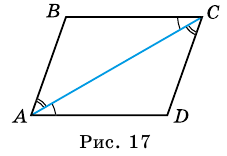
Доказательство:

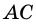
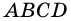
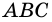
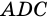
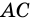
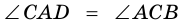
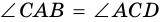
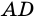
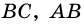
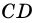
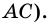
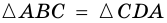
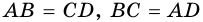
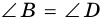
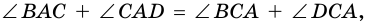
Диагональ разбивает параллелограмм на два треугольника и (рис. 17). -их общая сторона, и (как внутренние накрест лежащие углы для каждой из пар параллельных прямых и и и секущей Тогда (по стороне и двум прилежащим углам). Откуда, и (как соответственные элементы равных треугольников). Так как то

4. Периметр параллелограмма

5. Диагонали параллелограмма точкой пересечения делятся пополам.

Доказательство:

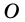
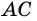
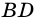
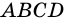
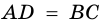
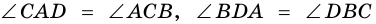
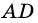
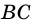
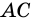
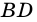
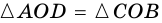
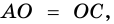
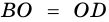
Пусть — точка пересечения диагоналей и параллелограмма (рис. 18). (как противолежащие стороны параллелограмма), (как внутренние накрест лежащие углы для параллельных прямых и и секущих и соответственно). Следовательно, (по стороне и двум прилежащим углам). Тогда (как соответственные стороны равных треугольников).

Пример:

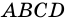
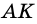
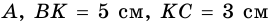
Дано: параллелограмм, — биссектриса угла (рис. 19). Найдите:

Решение:

1)

2) (как внутренние накрест лежащие углы для параллельных прямых и и секущей

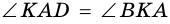
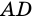
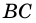
3) (по условию), тогда Тогда — равнобедренный (по признаку равнобедренного треугольника),

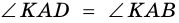
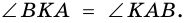
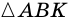
4)

Высотой параллелограмма называют перпендикуляр, проведенный из любой точки стороны параллелограмма к прямой, содержащей противолежащую сторону.

На рисунке 20 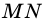— высота параллелограмма,

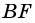
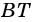
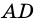
Из каждой вершины параллелограмма можно провести две высоты. Например, на рисунке 21 и — высоты параллелограмма, проведенные соответственно к сторонам и

Рассмотрим признаки параллелограмма.

Теорема (признаки параллелограмма). Если в четырехугольнике: 1) две стороны параллельны и равны, или 2) противолежащие стороны попарно равны, или 3) диагонали точкой пересечения делятся пополам, или 4) противолежащие углы попарно равны, — то четырехугольник является параллелограммом.

Доказательство:

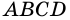
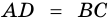
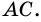
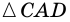
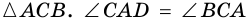
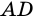
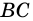
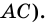
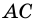
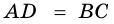
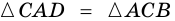
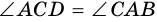
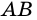
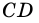
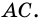
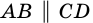
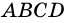
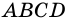
1) Пусть в четырехугольнике и (рис. 22). Проведем диагональ Рассмотрим и (как внутренние накрест лежащие при параллельных прямых и и секущей — общая сторона, (по условию). Следовательно, (по двум сторонам и углу между ними). Тогда (как соответственные). Но это накрест лежащие углы при пересечении прямых и секущей Поэтому (по признаку параллельности прямых). Следовательно, в четырехугольнике противолежащие стороны попарно параллельны. Поэтому -параллелограмм.

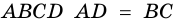
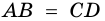
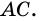
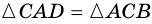
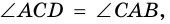
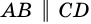
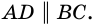
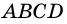
2) Пусть в четырехугольнике и (рис. 22). Проведем диагональ Тогда (по трем сторонам). Поэтому и следовательно, (по признаку параллельности прямых). Аналогично доказываем, что Следовательно, — параллелограмм.

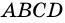
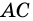
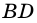
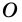
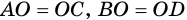
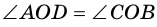
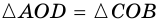
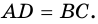
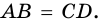
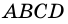
3) Пусть в четырехугольнике диагонали и пересекаются в точке и (рис. 23). (как вертикальные). Поэтому (по двум сторонам и углу между ними). Отсюда Аналогично доказываем, что Принимая во внимание п. 2) этой теоремы, приходим к выводу, что — параллелограмм.

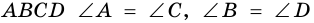
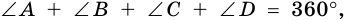
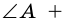
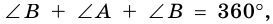
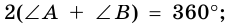
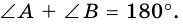
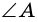
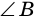
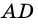
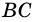
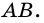
4) Пусть в параллелограмме (рис. 16). Так как то т. е. откуда Но и — внутренние накрест лежащие углы для прямых и и секущей Поэтому

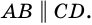
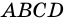
по признаку параллельности прямых). Аналогично доказываем, что Следовательно, — параллелограмм.

Пример:

В четырехугольнике 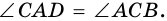Докажите, что — параллелограмм.

Доказательство:

Пусть — данный четырехугольник (рис. 22). Рассмотрим и — их общая сторона, (по условию). Тогда, (по двум сторонам и углу между ними). Следовательно, Но тогда в четырехугольнике противолежащие стороны попарно равны, поэтому он является параллелограммом.

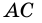
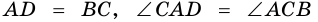
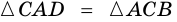
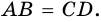
О некоторых видах четырехугольников (квадраты, прямоугольники, равнобокие и прямоугольные трапеции) знали еще древнеегипетские и вавилонские математики.

Термин «параллелограмм» греческого происхождения, считают, что он был введен Евклидом (около 300 г. до н. э.). Также известно, что еще раньше о параллелограмме и некоторых его свойствах уже знали ученики школы Пифагора («пифагорейцы»).

В «Началах» Евклида доказана следующая теорема: в параллелограмме противолежащие стороны равны и противолежащие углы равны, а диагональ делит его пополам, но не упоминается о том, что точка пересечения диагоналей параллелограмма делит каждую из них пополам.

Евклид также не упоминает ни о прямоугольнике, ни о ромбе.

Полная теория параллелограммов была разработана лишь в конце Средневековья, а в учебниках она появилась в XVII в. Все теоремы и свойства параллелограмма в этих учебниках основывались на аксиоме параллельности Евклида.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

378 Докажите Что Параллелограмм Является Выпуклым Четырехугольником

Загрузил: Геометрия с нуля

Длительность: 58 сек

11 Даны Прямая И Точка Не Лежащая На Этой Прямой Докажите Что Все Прямые Проходящие Через

Миникурс По Геометрии Четырехугольники

8 Класс 4 Урок Параллелограмм

46 Прямая M Параллельна Диагонали Bd Ромба Abcd И Не Лежит В Плоскости Ромба

121 В Треугольнике Abc Дано C 90 Ac 6 См Вс 8 См См Медиана Через Вершину С

В Параллелограмме Противоположные Углы Равны 8Кл Теорема

Школьная математика. Дистанционное обучение.

390 Один Из Углов Равнобедренной Трапеции Равен 68 Найдите Остальные Углы

150 Через Вершину А Прямоугольника Abcd Проведена Прямая Ак Перпендикулярная К Плоскости

Геометрия 8 Урок 2 Параллелограмм Свойства И Признаки

45 Прямая А Параллельна Стороне Вс Параллелограмма Abcd И Не Лежит В Плоскости Параллелограмма

759 Дан Произвольный Четырехугольник Mnpq Докажите Что

112 Докажите Что Сумма Квадратов Четырех Диагоналей Параллелепипеда Равна Сумме Квадратов Двенадц

35 Через Точку М Не Лежащую На Прямой А Проведены Две Прямые Не Имеющие Общих Точек С Прямой А

375 Найдите Периметр Параллелограмма Если Биссектриса Одного Из Его Углов Делит

44 Прямые Ов И Cd Параллельные А Оа И Cd Скрещивающиеся Прямые

61 Даны Пересекающиеся Прямые А И B И Точка А Не Лежащая В Плоскости Этих Прямых

107 Изобразите Тетраэдр Abcd И Отметьте Точку М На Ребре Ав Постройте Сечение Тетраэдра Плоскость

Четырехугольники Вебинар Математика

568 Докажите Что Четырехугольник Ромб Если Его Вершинами Являются Середины Сторон

Куинн Группа Лучшее

Аллилуйя Красивая Музыка Саксофон Скрипка

Slendytubbies 3 Run Away

Стивен Кинг Подборка Музыки Для Чтения

Ната Недина Все Песни

Gaster S Theme Orchestral

Chris Brown Go Crazy Remix Ft Young Thug Future Lil Durk Latto Lyrics 8D Audio

Berita Dari Masjidil Haram Hari Ini Tanggal 15 November 2021 Ibadah Umrah Sutaryo Hatmosuwiryo

Гранатовый Браслет 46 42 56 30

Стрим Warface Варфейс На Дворе Декабрь Ждемс Новый Год И Новое Обновление

Bachata Instrumental 2021 Solita Beat Bachata Drill Bachadrill

Gumball My Demons Mv

Шокирующие Результаты Проверки Адеева На Детекторе Дом 2 Новости И Слухи 07 05 2021

Persekutuan Doa Rabu 3 Maret 2021

Who S The Real Singer Meme Mlb Original Plot Twist

Prn Melaka Lima Dun Jadi Perhatian Tampilkan Calon Heavyweight

Akhirnya Penyelamat Karir Billy Gilmour Datang Barkley Tak Boleh Disalahkan Milan Incar Bek Chelsea

Александр Николин Группа Москва Перелетная Птица

Kegiatan Sehari Hari Ibu Rumah Tangga Masak 2 Menu

Duet Challenge Derpy Axolotl

Mekhman Копия Пиратская

Loboda Новый Рим Live Авторадио

Free Pierre Bourne X Kingdom Hearts X Slump Ak Type Beat Heartless

My Demons But All Fnaf Characters Sing It

American Boy Prank Videos Funny Reaction Tiktok Meme Shorts Activefunny

Im So Lucky Lucky Edit Inquisitormaster Thesquad Alevi Edit

Shania Twain Self Titled 1993 By Shania Twain First Listen Album Review

Источник

Как доказать, что четырехугольник является параллелограммом?

Согласно определению,геометрическая фигура параллелограмм является четырехугольником с попарно параллельными противоположными сторонами и равными противолежащими углами. Доказать, что фигура параллелограмм позволяет как определение, так и ее признаки. Применяя на практике эти свойства, можно решать геометрические задачи разной сложности.

Определение параллелограмма

Четырехугольник является параллелограммом с параллельными противоположными сторонами. Эта фигура имеет по 2 тупых и острых угла, произвольную величину которых определяют при решении задач. Для этого используют не только признаки параллелограмма или треугольника, но и таблицу синусов с косинусами.

Квадрат, прямоугольник и ромб — это параллелограммы, обладающие общими свойствами. Фигура, у которой диагонали совпадают с биссектрисами, является ромбом. Согласно определению, прямоугольник — это четырехугольник, имеющий все прямые углы. Если стороны этой фигуры равны между собой, то прямоугольник является квадратом.

Параллелограмм — геометрическая фигура с равными противоположными сторонами. Если каждую из них возвести в квадрат и сложить их между собой, то полученная величина будет равна сумме квадратов диагоналей, проведенных через противоположные вершины углов фигуры. Диагонали этого четырехугольника пересекаются в точке, определить которую позволяют прямоугольные координаты.

Свойства фигуры

Зная различные свойства четырехугольников, можно решать простые и сложные задачи по геометрии, начиная с определения периметра, заканчивая нахождением координаты вершины параллелограмма. Для решения задач используют 7 основных свойств параллелограмма, учитывая что его стороны попарно образуют:

Доказать последнее свойство позволяет II признак равенства треугольников. Известен отрезок, принадлежащий линии, проведенной через точку, в которой пересекаются диагонали. В четырехугольнике КМРТ он обозначен НП. Отсюда следует равенство треугольников КОП и НОР, поэтому НО=ОП.

Сумма смежных углов параллелограмма составляет 180 градусов, поскольку они являются односторонними при параллельных прямых. Существует свойство равенства острого угла и образованного высотами тупого угла четырехугольника АВСД. Параллелограмм имеет смежные углы А и Д, а высоты ВМ и ВН проведены из вершины В, поэтому угол МВН в сумме с Д равен 180 градусам.

Доказательство равенства противолежащих сторон и углов фигуры заключается в следующем. Например, диагонали ABCD делят фигуру на 2 равных треугольника, имеющих общую сторону в виде диагонали BD. При этом углы ADВ и ABC при противолежащих вершинах A и C являются накрест лежащими.

Параллелограмм состоит из равных треугольников ABD, BCD и ABC, ACD, образуемых диагоналями AC и ВD, значит AB=CD и AD=BC. Отсюда углы при вершинах A и C, В и D имеют одинаковую величину.

Свойства можно представить в виде формул для решения уравнений и примеров, а также доказать теоретически. Их следует запомнить, чтобы правильно применять на практике. Для решения более сложных задач по геометрии следует доказать основные свойства фигуры.

Основные признаки

Существует 5 признаков параллелограмма, доказательство которых основано на свойствах прямых и образованных ими углов либо фигур. Выпуклый четырехугольник, вершины которого обозначены МНКП, имеет диагонали МП и НК. Признаки того, что фигура МНКП представляет собой параллелограмм, следующие:

Если четырехугольник имеет 2 равные и параллельные стороны, то он представляет собой параллелограмм. Четырехугольник MNPK имеет параллельные и равные MN и KP, отсюда следует доказательство I признака:

Если четырехугольник имеет противоположные стороны, которые равны попарно, то он является параллелограммом. Перед тем как доказать, что фигура является параллелограммом, следует провести диагонали. Пошаговое доказательство II признака:

Доказать деление точкой пересечения каждой из диагоналей фигуры АМКД на равные отрезки позволяет II признак равенства треугольников. При этом AОД и КОМ равны. Следовательно, AО=КО и АО=ДО.

Согласно III признаку, четырехугольник, диагонали которого пересекаются, а точка пересечения делит их пополам, представляет собой параллелограмм. В четырехугольнике MNPQ она обозначена буквой К. Поскольку в ней пересекаются диагонали MP и NQ, то образуемые ими треугольники MNК и КPQ равны по I признаку. Это следует из равенства вертикальных углов MКN и PКQ, а также MК и NК, КP и КQ, которые равны по условию.

В треугольниках MNК и КPQ стороны MN и PQ равны между собой. Углы NMК и КPQ равны как накрест лежащие при MN и PQ и секущей MP. Отсюда следует, что прямые MN||PQ. Итак, четырехугольник MNPQ — это параллелограмм по I признаку, поскольку MN и PQ равны и параллельны.

Пошаговое доказательство

Перед тем как доказать, что четырехугольник параллелограмм, нужно провести высоты треугольников МНК и МПК, пересекающие МК в точках О и С. По данным задачи, МНК, МПК и НПК имеют одинаковые площади. Доказательство параллельности МК и НП состоит из следующих шагов:

Чтобы доказать, что МН и ПК параллельны, нужно опустить из вершин треугольников МНК и НКП высоты Н и П, которые пересекут прямую ПК в точках Р и Т. По построению НР=ПТ, а по указанному условию площади треугольников МНК и НПК совпадают. Сторона МН параллельна ПК, следовательно, МНПК — параллелограмм. Итак, порядок доказательства параллельности МН и ПК аналогичен с доказательством, что МК и НП параллельны.

Доказательство признака образования равнобедренного треугольника и трапеции при пересечении противолежащей стороны параллелограмма биссектрисой АМ одного из углов состоит из следующих утверждений:

Зная, как доказать, что фигура параллелограмм, если известно, что 2 из его сторон равны и параллельны, можно использовать I признак равенства для доказательства другого. Согласно II признаку, стороны параллелограмма попарно равны между собой.

Источник