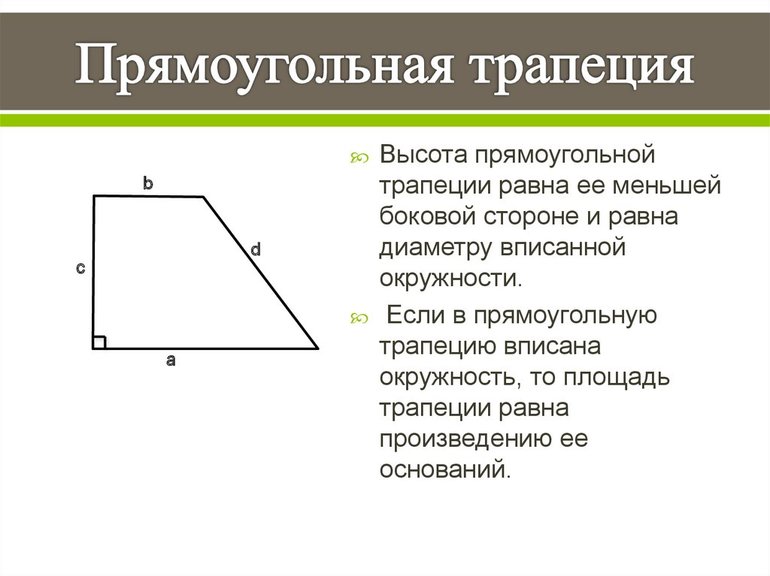
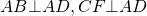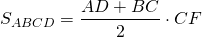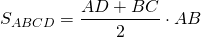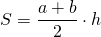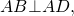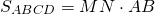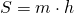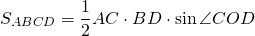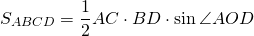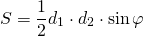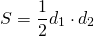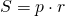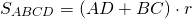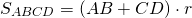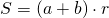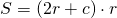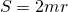Докажите что площадь прямоугольной трапеции
Площадь прямоугольной трапеции
Площадь прямоугольной трапеции можно найти по любой из формул для площади произвольной трапеции. Некоторые из общих формул могут быть упрощены на основании свойств прямоугольной трапеции.
I. Площадь трапеции равна произведению полусуммы оснований на высоту.
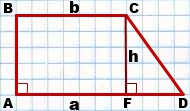
Так как меньшая боковая сторона прямоугольной трапеции перпендикулярна основаниям, то она равна высоте трапеции, то есть
Если обозначить AD=a, BC=b, CF=AB=h, то формула площади прямоугольной трапеции через основания и высоту (меньшую боковую сторону):
II. Площадь трапеции равна произведению средней линии на высоту.

Если обозначить среднюю линию MN=m, меньшую боковую сторону AB=h, получим формулу для нахождения площади прямоугольной трапеции через среднюю линию:
III. Площадь трапеции равна половине произведения диагоналей трапеции на синус угла между ними.

Если AC=d1, BD=d2, ∠COD=φ, то

VI. Площадь трапеции равна произведению её полупериметра на радиус вписанной окружности.
Обозначив AD=a, BC=b, CD=c, AB=h=2r, получим формулы площади прямоугольной трапеции через радиус вписанной окружности:
Если в трапецию вписана окружность, площадь трапеции также можно найти как удвоенное произведение радиуса и средней линии. Формула
Если в прямоугольную трапецию вписана окружность, ее площадь равна произведению оснований.
Трапеция
Трапеция — это выпуклый четырёхугольник, у которого две противолежащие стороны параллельны друг другу, а две другие не параллельны. Параллельные стороны трапеции называются основаниями, а две другие — боковыми сторонами или боками.
Отрезок, перпендикулярный основаниям трапеции, называется высотой. Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией.
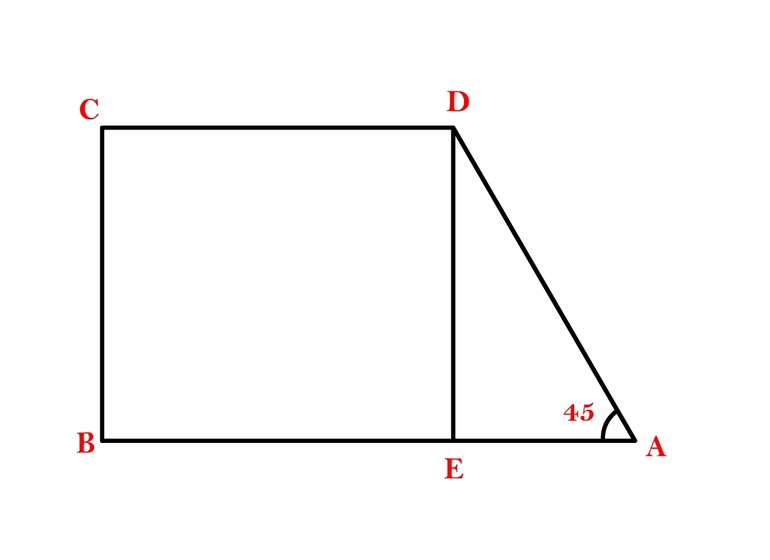
Трапеция может быть равнобедренной или прямоугольной. Равнобедренная (или равнобокая) трапеция — это трапеция, у которой боковые стороны равны. Прямоугольная трапеция — это трапеция, у которой одна из боковых сторон перпендикулярна основаниям.
Площадь трапеции
Площадь трапеции равна произведению полусуммы оснований на высоту.
Формула площади трапеции:
где S — это площадь трапеции, a и b — основания трапеции, h — высота трапеции.
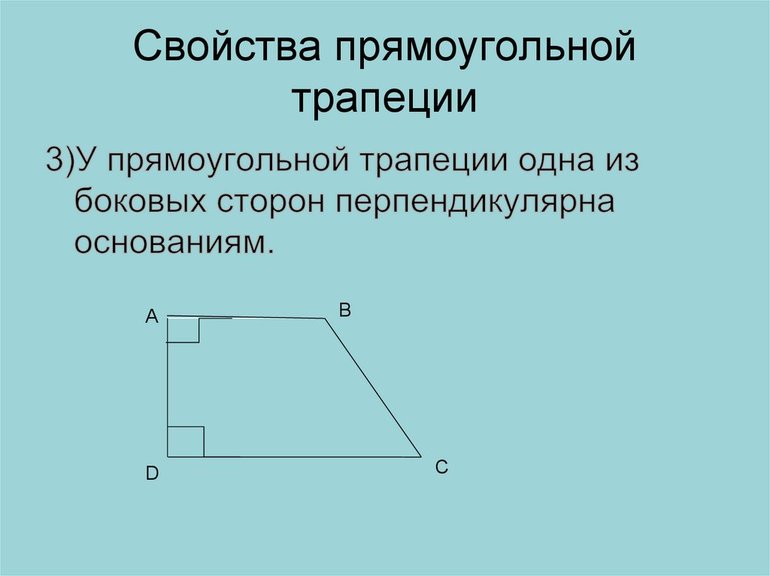
Доказательство. Разделим трапецию на два треугольника, проведя диагональ BD. Получилось два треугольника ΔABD и ΔBCD, имеющих одинаковую высоту — h и основания a и b:
Площади этих треугольников будут вычисляться по следующим формулам:
| S1 = | 1 | ah, S2 = | 1 | bh. |
| 2 | 2 |
Площадь трапеции будет равна сумме площадей треугольников, из которых она состоит, следовательно:
Площадь прямоугольной трапеции через угол и основания
Следующей после треугольника по сложности фигурой, которую изучают в школьной программе геометрии, является трапеция. Многие задачи с ее участием связаны с определением периметра и площади. В прямоугольной трапеции через угол и основания можно рассчитать обе эти величины, применяя теорему Пифагора.
Особенности и свойства трапеций
Прежде чем разобраться, как найти площадь прямоугольной трапеции, следует подробнее рассмотреть свойства этого класса фигур. Все они представляют собой выпуклые четырехугольники, у которых две и всего две стороны параллельны между собой. Они называются основаниями и имеют разную длину. Оставшиеся две стороны наклонены друг относительно друга под определенным и неравным нулю углом. Они называются боковыми.
Нетрудно догадаться, что основания фигуры должны всегда отличаться по длине. В противном случае параллельными между собой окажутся также боковые стороны, и получится не трапеция, а прямоугольник или квадрат.
Терминология и элементы
Из определения трапеции следует, что эта фигура состоит из двух оснований и двух боковых сторон. Помимо них, в геометрии выделяют также следующие линейные характеристики:
Все формулы для нахождения длин соответствующих линейных элементов трапеции справедливы независимо от значений ее сторон и внутренних углов.
Существующие типы
Несмотря на простоту построения трапеции, она бывает нескольких типов. Последние определяются однозначно с учетом значения внутренних углов фигуры. В геометрии выделяют следующие типы:
Для всех перечисленных типов трапеции справедлив тот факт, что сумма четырех углов составляет 360 °. В любой тип фигуры можно вписать окружность. Для этого необходимо, чтобы выполнялось следующее условие:
Другими словами, сумма длин оснований должна быть в точности равна сумме боковых сторон.
Прямоугольная фигура и ее характеристики
Несмотря на невысокую симметрию трапеции с прямыми углами, работать с ней удобно при решении задач, поскольку можно напрямую использовать теорему Пифагора.
Пусть имеется фигура, в которой a и b — это основания, c — сторона, которая им обоим перпендикулярна и образует с ними прямые внутренние углы, d — боковая сторона, которая наклонена под некоторым углом к основаниям. Из такого построения ясно, что боковая сторона c также является высотой h фигуры.
Углы и диагонали
Формулы для расчета внутренних углов и длин диагоналей в прямоугольной фигуре имеют простой вид. Чтобы найти тупой и острый углы, достаточно рассмотреть прямоугольный треугольник, который образован следующими отрезками:
Нетрудно доказать, что синус острого угла α при основании может быть рассчитан по следующей формуле:
Поскольку вместе с тупым углом β он составляет 180 °, тогда справедливы равенства:
sin (α) = sin (β) = c/d и β = 180 ° — α.
Для вычисления диагоналей прямоугольной трапеции можно воспользоваться общими формулами для D1 и D2.
Однако, для этого типа фигуры их можно упростить, воспользовавшись теоремой Пифагора. Любая из проведенных диагоналей образует внутри рассматриваемой трапеции прямоугольный треугольник, поэтому для D1 и D2 можно записать следующие равенства:
Для вычисления диагоналей D1 и D2 необязательно знать длину боковой стороны d.
Вычисление площади
Существует несколько выражений, используя которые можно определить площадь любой трапеции. Для прямоугольной фигуры все эти формулы имеют упрощенный вид. В первую очередь следует отметить общее выражение для площади S, которая равна произведению медианы M на высоту h:
Для прямоугольной трапеции эта формула преобразуется в следующее равенство:
Удобно определять площадь рассматриваемой фигуры также через ее диагонали D1, D2 и угол их пересечения γ. Эта формула имеет вид:
То есть половина произведения диагоналей на синус угла их пересечения дадут площадь всей фигуры. Необходимо отметить, что неважно, какой брать угол (острый или тупой) они связаны друг с другом (в сумме дают 180 °) и их синусы равны. Если диагонали пересекаются под прямым углом, то формула для S сводится к выражению:
Существует еще одна формула площади трапеции прямоугольной через ее основания a, b и острый угол α. Применяя следующие рассуждения и выкладки можно ее получить:
Аналогичную формулу можно использовать, если известен не острый угол α, а тупой β. В этом случае выражение для S примет вид:
Функция tg (β) здесь является отрицательной величиной, поэтому вычитаемое и уменьшаемое в множителе a-b поменялись местами. Все выражения для расчета площади применимы при определении объема призм в трехмерном пространстве, у которых основания представляют собой трапеции.
Примеры решения задач
Пример 1. Пусть задана прямоугольная трапеция, медиана которой равна 12 см и острый угол при основании составляет 45 °. Также известно, что боковая сторона, которая не является высотой, составляет 10 см. Необходимо рассчитать площадь этой фигуры.
Если рассмотреть треугольник прямоугольный, который образован двумя боковыми сторонами и заданным острым углом, то можно рассчитать высоту фигуры:
h = d*sin (α) = 10*sin (45 °) = 7,071 см.
Поскольку из условия задачи известна медиана, то можно применить общую формулу для определения площади трапеции:
Любопытно отметить, что для решения этой задачи не понадобилось знать длины каждого из оснований.
Пример 2. Известно, что большее из оснований трапеции прямоугольной имеет длину 12 см, ее наклонная сторона равна 10 см, а угол при основании составляет 53,13 °. Необходимо выяснить, как найти площадь прямоугольной трапеции из этих данных.
Для решения задачи удобно использовать следующие общепринятые обозначения:
Рассматривая треугольник с прямым углом, который заключен между сторонами b-a, d и c, можно вычислить все неизвестные длины отрезков:
Общая формула для площади трапеции приобретает вид:
S = M*h = (a+b)/2*c = (2*b — d*cos (α))*d*sin (α)/2.
Пример 3. Известно, что в трапеции с прямыми углами диагонали составляют 7 см и 11 см, высота фигуры равна 5 см. Необходимо найти ее площадь.
Из теоремы Пифагора следует, что каждое из оснований трапеции может быть вычислено следующим образом:
Таким образом, прямоугольная трапеция является простой фигурой, для вычисления площади которой удобно воспользоваться теоремой Пифагора. Существуют несколько формул для определения величины S, параметрами которых являются длины сторон и непрямые углы.
Площадь прямоугольной трапеции через угол и основания
Особенности и свойства трапеций
Прежде чем разобраться, как найти площадь прямоугольной трапеции, следует подробнее рассмотреть свойства этого класса фигур. Все они представляют собой выпуклые четырехугольники, у которых две и всего две стороны параллельны между собой. Они называются основаниями и имеют разную длину. Оставшиеся две стороны наклонены друг относительно друга под определенным и неравным нулю углом. Они называются боковыми.
Нетрудно догадаться, что основания фигуры должны всегда отличаться по длине. В противном случае параллельными между собой окажутся также боковые стороны, и получится не трапеция, а прямоугольник или квадрат.
Терминология и элементы
Из определения трапеции следует, что эта фигура состоит из двух оснований и двух боковых сторон. Помимо них, в геометрии выделяют также следующие линейные характеристики:
Все формулы для нахождения длин соответствующих линейных элементов трапеции справедливы независимо от значений ее сторон и внутренних углов.
Существующие типы
Несмотря на простоту построения трапеции, она бывает нескольких типов. Последние определяются однозначно с учетом значения внутренних углов фигуры. В геометрии выделяют следующие типы:
Для всех перечисленных типов трапеции справедлив тот факт, что сумма четырех углов составляет 360 °. В любой тип фигуры можно вписать окружность. Для этого необходимо, чтобы выполнялось следующее условие:
Другими словами, сумма длин оснований должна быть в точности равна сумме боковых сторон.
Прямоугольная фигура и ее характеристики
Несмотря на невысокую симметрию трапеции с прямыми углами, работать с ней удобно при решении задач, поскольку можно напрямую использовать теорему Пифагора.
Пусть имеется фигура, в которой a и b — это основания, c — сторона, которая им обоим перпендикулярна и образует с ними прямые внутренние углы, d — боковая сторона, которая наклонена под некоторым углом к основаниям. Из такого построения ясно, что боковая сторона c также является высотой h фигуры.
Углы и диагонали
Формулы для расчета внутренних углов и длин диагоналей в прямоугольной фигуре имеют простой вид. Чтобы найти тупой и острый углы, достаточно рассмотреть прямоугольный треугольник, который образован следующими отрезками:
Нетрудно доказать, что синус острого угла α при основании может быть рассчитан по следующей формуле:
Поскольку вместе с тупым углом β он составляет 180 °, тогда справедливы равенства:
Для вычисления диагоналей прямоугольной трапеции можно воспользоваться общими формулами для D1 и D2.
Однако, для этого типа фигуры их можно упростить, воспользовавшись теоремой Пифагора. Любая из проведенных диагоналей образует внутри рассматриваемой трапеции прямоугольный треугольник, поэтому для D1 и D2 можно записать следующие равенства:
Для вычисления диагоналей D1 и D2 необязательно знать длину боковой стороны d.
Вычисление площади
Существует несколько выражений, используя которые можно определить площадь любой трапеции. Для прямоугольной фигуры все эти формулы имеют упрощенный вид. В первую очередь следует отметить общее выражение для площади S, которая равна произведению медианы M на высоту h:
Для прямоугольной трапеции эта формула преобразуется в следующее равенство:
Удобно определять площадь рассматриваемой фигуры также через ее диагонали D1, D2 и угол их пересечения γ. Эта формула имеет вид:
То есть половина произведения диагоналей на синус угла их пересечения дадут площадь всей фигуры. Необходимо отметить, что неважно, какой брать угол (острый или тупой) они связаны друг с другом (в сумме дают 180 °) и их синусы равны. Если диагонали пересекаются под прямым углом, то формула для S сводится к выражению:
Существует еще одна формула площади трапеции прямоугольной через ее основания a, b и острый угол α. Применяя следующие рассуждения и выкладки можно ее получить:
Аналогичную формулу можно использовать, если известен не острый угол α, а тупой β. В этом случае выражение для S примет вид:
Функция tg (β) здесь является отрицательной величиной, поэтому вычитаемое и уменьшаемое в множителе a-b поменялись местами. Все выражения для расчета площади применимы при определении объема призм в трехмерном пространстве, у которых основания представляют собой трапеции.
Примеры решения задач
Пример 1. Пусть задана прямоугольная трапеция, медиана которой равна 12 см и острый угол при основании составляет 45 °. Также известно, что боковая сторона, которая не является высотой, составляет 10 см. Необходимо рассчитать площадь этой фигуры.
Если рассмотреть треугольник прямоугольный, который образован двумя боковыми сторонами и заданным острым углом, то можно рассчитать высоту фигуры:
h = d*sin (α) = 10*sin (45 °) = 7,071 см.
Поскольку из условия задачи известна медиана, то можно применить общую формулу для определения площади трапеции:
Любопытно отметить, что для решения этой задачи не понадобилось знать длины каждого из оснований.
Пример 2. Известно, что большее из оснований трапеции прямоугольной имеет длину 12 см, ее наклонная сторона равна 10 см, а угол при основании составляет 53,13 °. Необходимо выяснить, как найти площадь прямоугольной трапеции из этих данных.
Для решения задачи удобно использовать следующие общепринятые обозначения:
Рассматривая треугольник с прямым углом, который заключен между сторонами b-a, d и c, можно вычислить все неизвестные длины отрезков:
Общая формула для площади трапеции приобретает вид:
S = M*h = (a+b)/2*c = (2*b — d*cos (α))*d*sin (α)/2.
Пример 3. Известно, что в трапеции с прямыми углами диагонали составляют 7 см и 11 см, высота фигуры равна 5 см. Необходимо найти ее площадь.
Из теоремы Пифагора следует, что каждое из оснований трапеции может быть вычислено следующим образом:
Таким образом, прямоугольная трапеция является простой фигурой, для вычисления площади которой удобно воспользоваться теоремой Пифагора. Существуют несколько формул для определения величины S, параметрами которых являются длины сторон и непрямые углы.
Докажите что площадь прямоугольной трапеции
Напомним свойства трапеции, которые часто используются при решении задач. Некоторые из этих свойств были доказаны в заданиях для 9-го класса, другие попробуйте доказать самостоятельно. Приведённые рисунки напоминают ход доказательства.
$$ 4.<2>^<○>$$. В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжении боковых сторон, лежат на одной прямой (на рис. 21 точки `M`, `N`, `O` и `K`).
$$ 4.<3>^<○>$$. В равнобокой трапеции углы при основании равны (рис. 22).
$$ 4.<4>^<○>$$. В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции (рис. 23).
$$ 4.<5>^<○>$$. В равнобокой трапеции диагонали равны (рис. 24).
$$ 4.<6>^<○>$$. В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой – их полусумме
(рис. 25, основания равны `a` и `b`, `a>b`).
$$ 4.<7>^<○>$$. Во всякой трапеции середины боковых сторон и середины диагоналей лежат на одной прямой (рис. 26).
$$ 4.<8>^<○>$$. Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований (рис. 27).
Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований, т. е. `d_1^2+d_2^2=c_1^2+c_2^2+2*ab`.
$$ 4.<10>^<○>$$. Во всякой трапеции с основаниями `a` и `b` отрезок с концами на боковых сторонах, проходящий через точку пересечения диагоналей параллельно основаниям, равен `(2ab)/(a+b)` (на рис. 28 отрезок `MN`).
$$ 4.<11>^<○>$$. Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.
Применяем теорему косинусов (см. рис. 29а и б):
`ul(DeltaACD):` `d_1^2=a^2+c_2^2-2a*c_2*cos varphi`,
`ul(DeltaBCD):` `d_2^2=b^2+c_2^2+2b*c_2*cos varphi` (т. к. `cos(180^@-varphi)=-cos varphi`).
Проводим `CK«|\|«BA` (рис. 29в), рассматриваем треугольник `ul(KCD):` `c_1^2=c_2^2+(a-b)^2-2c_2*(a-b)*cos varphi`. Используя последнее равенство, заменяем выражение в скобках в (2), получаем:
| `d_1^2+d_2^2=c_1^2+c_2^2+2ab`. |
В случае равнобокой трапеции `d_1=d_2`, `c_1=c_2=c`, поэтому получаем
Отрезок, соединяющий середины оснований трапеции, равен `5`, одна из диагоналей равна `6`. Найти площадь трапеции, если её диагонали перпендикулярны.
Прямоугольный треугольник `ul(BDK)` с гипотенузой `BK=BC+AD=2MN=10` и катетом `DK=6` имеет площадь `S=1/2DK*BD=1/2DKsqrt(BK^2-DK^2)=24`. Но площадь треугольника `BDK` равна площади трапеции, т. к. если `DP_|_BK`, то
Диагонали трапеции, пересекаясь, разбивают её на четыре треугольника с общей вершиной. Найти площадь трапеции, если площади треугольников, прилежащих к основаниям, равны `S_1` и `S_2`.
Далее, треугольники `BOC` и `DOA` подобны, площади подобных треугольников относятся как квадраты соответствующих сторон, значит, `(S_1)/(S_2)=(a/b)^2`. Таким образом, `(S_0+S_1)/(S_0+S_2)=sqrt((S_1)/(S_2))`.Отсюда находим `S_0=sqrt(S_1S_2)`, и поэтому площадь трапеции будет равна
Основания равнобокой трапеции равны `8` и `10`, высота трапеции равна `3` (рис. 32).
Найти радиус окружности, описанной около этой трапеции.
Из прямоугольного треугольника `ABK` находим `AB=sqrt(1+9)=sqrt(10)` и `sinA=(BK)/(AB)=3/(sqrt10)`. Окружность, описанная около трапеции `ABCD`, описана и около треугольника `ABD`, значит (формула (1), § 1), `R=(BD)/(2sinA)`. Отрезок `BD` находим из прямоугольного треугольника `KDB:` `BD=sqrt(BK^2+KD^2)=3sqrt(10)` (или по формуле `d^2=c^2+ab`), тогда
$$ 4.<12>^<○>$$. Площадь трапеции равна площади треугольника, две стороны которого равны диагоналям трапеции, а третья равна сумме оснований.