Докажите что подпространство сепарабельного метрического пространства также сепарабельно

Как доказать, что подпространство сепарабельного пространство сепарабельно?

Для произвольных топологических пространств это не так. Контрпример можно найти в книге американских математиков Б. Гелбаума и Дж. Олмстеда «Контрпримеры в анализе» (русский перевод вышел в издательстве Мир в 1967 году)

Прежде, чем привести контрпример, обсудим его идею. По определению пространство называется сепарабельным, если оно содержит счётное всюду плотное подмножество. Например, отрезок вещественной прямой в топологии, порожденной евклидовой метрикой содержит счётное всюду плотное подмножество, состоящее из всех рациональных точек этого отрезка. А что будет со свойством сепарабельности, если мы выбросим все рациональные точки? Найдётся ли новое всюду плотное подмножество?

Контрпример из книги обходит этот вопрос следующим образом:

Рассмотрим тот же отрезок вещественной прямой, но зададим на нём топологию, в которой открытыми множествами являются множества, состоящие из рациональных точек открытых окрестностей точек и самих этих точек. Легко проверить, что заданная таким образом система множеств действительно задаёт топологию.

Если теперь мы выбросим из нашего отрезка все рациональные точки, т о индуцированная на получившемся подпространстве топология будет дискретной, а подпространство несепарабельным.

Иначе обстоит дело в метрических пространствах. В метрических пространствах сепарабельность эквивалентна существованию счётной базы топологии. В одну сторону это свойство почти очевидно: возьмите по точке в каждом множестве счётной базы топологии и получите всюду плотное множество. В другую сторону его тоже не сложно проверить: возьмите счётное всюду плотное множество S и проверьте, что все шары рациональных радиусов с центрами в точках множества S. Образуют базу топологии. Базу индуцированной топологии подпространства образуют пересечения элементов базы топологии объемлющего пространства с этим подпространством, следовательно любое подпространство сепарабельного метрического пространства имеет счётную базу, то есть является сепарабельным.

В записках Александра Шеня по курсу анализа есть задача: доказать сепарабельность подпространства сепарабельного метрического пространства, не пользуясь понятием счетной базы. Попробуйте это сделать.

Источник

Докажите что подпространство сепарабельного метрического пространства также сепарабельно

Пусть А — некоторое множество в нормированном пространстве В. Это множество называется плотным а пространстве В, если любой шар содержит хотя бы одну точку этого множества.

Отсюда что А плотно в В тогда и только тогда, когда для любого элемента и любого числа существует вектор такой, что

Пусть в пространстве В задана последовательность векторов

Эта последовательность называется полной в В, если ее линейная оболочка плотна в пространстве В. Из определения линейной оболочки (см. п. 2.9) последовательности векторов заключаем, что последовательность (7.1) является полной тогда и только тогда, когда для любого элемента и любого числа найдется линейная комбинация векторов (7.1) такая, что

Нормированное пространство, в котором существуют полные последовательности, называется сепарабельным. Большинство важнейших пространств, встречающихся в математической физике, являются сепарабельными.

Покажем, что в каждом сепарабельном пространстве существует полная линейно-независимая последовательность векторов. Действительно, если последовательность (7.1) не является линейно-независимой, то ее можно сделать таковой, последовательно вычеркивая векторы, которые являются линейными комбинациями предыдущих. Предоставляем читателю самостоятельно это доказать. Ясно, что линейная оболочка полученной последовательности векторов совпадает с линейной оболочкой векторов (7.1). Поэтому полеченная последовательность векторов является полной.

Пример. Последовательность полна в пространстве С. Это следует из теоремы Вейерштрасса о том, что для каждой непрерывной функции на отрезке [0, 1] и любого положительного числа существует полином такой, что для всех [0, 1]. Таким образом, пространство С является сепарабельным.

Источник

Сепарабельность

В топологии и смежных областях математики сепара́бельным пространством (от лат. separabilis — отделимый) называется топологическое пространство, в котором содержится не более чем счётное всюду плотное множество.

Очень многие классические пространства, встречающиеся в математическом анализе и геометрии, являются сепарабельными. Сепарабельные пространства обладают некоторыми привлекательными для математиков свойствами. Многие из этих свойств проистекают из возможности представить каждый элемент пространства как предел последовательности элементов из счётного плотного множества, подобно тому как всякое действительное число можно представить как предел последовательности из рациональных чисел.

Многие теоремы могут быть доказаны конструктивно только для сепарабельных пространств. Типичным примером такой теоремы является теорема Хана — Банаха, которая в случае сепарабельных пространств может быть доказана конструктивно, но в противном случае использует для доказательства аксиому выбора.

Свойства

Примеры

См. также

Полезное

Смотреть что такое «Сепарабельность» в других словарях:

Сепарабельность актива — (asset separability) C.а. означает, что актив может быть отделен или выделен из (напр., вновь приобретенной) хозяйственной единицы и продан, перемещен, передан по лицензии, сдан в аренду или обменен (независимо от того, существуют ли вообще такие … Экономико-математический словарь

Сепарабельность функции — [se­­parability of function] в случае функции нескольких пе­ременных (аргументов) возможность разделения влияния аргументов на общий результат. Например, функция f (x1, …, xn) = ∑fi(xi), i = 1, …, n сепарабельная, поскольку каждое… … Экономико-математический словарь

сепарабельность актива — C.а. означает, что актив может быть отделен или выделен из (напр., вновь приобретенной) хозяйственной единицы и продан, перемещен, передан по лицензии, сдан в аренду или обменен (независимо от того, существуют ли вообще такие намерения).… … Справочник технического переводчика

Линейная сепарабельность — Два множества не разделимых линейно в … Википедия

Топологическое пространство — У этого термина существуют и другие значения, см. Пространство. Топологическое пространство основной объект изучения топологии (термин «топология» в его рамках см. ниже). Исторически, понятие топологического пространства появилось как … Википедия

Сепарабельное пространство — (от лат. separabilis отделимый) топологическое пространство, содержащее конечное или счётное всюду плотное множество. Многие пространства, возникающие в математическом анализе и геометрии, являются сепарабельными. Сепарабельные… … Википедия

Многослойный перцептрон Румельхарта — У этого термина существуют и другие значения, см. Многослойный перцептрон. Архитектура многослойного перцептрона Многослойный перцептрон частный случай перцептрона Розенблатта, в котором один алгоритм обратного распространения … Википедия

С — Сальдо (balance) Cальдо внешней торговли [balance of trade] Сальдо государственного бюджета [balance of state bud­get] Сальдо торгового баланса см. Сальдо внешней … Экономико-математический словарь

БАЗИС — множества X минимальное порождающее его подмножество В. Порождение означает, что применением операций нек рого класса к элементам получается любой элемент Это понятие связано с понятием зависимости: элементы Xпосредством операций из ставятся в… … Математическая энциклопедия

Источник

Научный форум dxdy

Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки

Правила форума

В этом разделе нельзя создавать новые темы.

Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».

Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.

Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.

Доказать сепарабельность замкнутого линеала

Заслуженный участник

Последний раз редактировалось ewert 14.11.2010, 18:47, всего редактировалось 1 раз.

Рассмотрите проекции элементов исходного базиса на подпространство (т.е. результаты действия на элементы базиса ортопроектора на это подпространство). Любой элемент подпространства будет раскладываться в сходящийся ряд по этим проекциям (вообще говоря, неоднозначно, но какая разница).

Последний раз редактировалось moscwicz 14.11.2010, 18:50, всего редактировалось 1 раз.

Последний раз редактировалось MetaMorphy 14.11.2010, 18:52, всего редактировалось 1 раз.

Как-то всё слишком сложно у вас.

(Upd.: выше уже предложили доказать гораздо более общее утверждение.)

Заслуженный участник

Заслуженный участник

Всё подобное. Ну нет у меня под рукой Канторовича с Акиловым. Я бы доказывал это так (скорее всего, и они примерно так же).

Заслуженный участник

Заслуженный участник

Я просто не понимаю, что такое «счётная база» в метрическом случае. Вы хотите сказать: доказывается, что метрическое пространство сепарабельно тогда и только тогда, когда оно сепарабельно, да.

Заслуженный участник

Последний раз редактировалось Padawan 14.11.2010, 20:49, всего редактировалось 1 раз.

ewert
Вы не беспокойтесь, нижеследующее не для Вас, а для интересующихся. Вас на этом форуме, как я заметил, все равно никому никогда ни в чем переубедить не удавалось. Такое случается с профессиональными педагогами.

Док-во.
Пусть — метрическое пространство и — плотное подмножество.

Пусть — какое-нибудбь подпространство, покажем, что оно сепарабельно.
Для каждого и для каждого выберем элемент
такой, что .
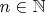
Очевидно, и есть плотное множество в . Действительно,
если то

Остается взять достаточно большим и подобрать так что бы был достаточно малым.

Заслуженный участник

Заслуженный участник

Заслуженный участник

А что Вы будете делать в том случае, когда это множество пусто? Например, на координатной плоскости множество точек, у которых обе координаты рациональны, всюду плотно. Прямая, задаваемая уравнением , не содержит ни одной точки, у которой обе координаты рациональны.

На самом деле это делается иначе. Я приведу другую конструкцию, которая реализует стандартное в топологии рассуждение Padawan а, не упоминая таких «страшных» понятий, как база и вес топологического пространства. Эта конструкция существенно не отличается от конструкции moscwicz (но моё изложение несколько более подробное).

Пусть — сепарабельное метрическое пространство с метрикой , — его подпространство, — счётное всюду плотное подмножество . Будем обозначать открытый шар радиуса 0$» title=»$\varepsilon>0$» /> с центром в точке и, аналогично, , но здесь .

Построение. Для каждой точки и каждого натурального рассмотрим множество . Если это множество не пусто, то выберем какую-нибудь точку . Совокупность всех выбранных точек обозначим . Очевидно, — счётное подмножество пространства . Осталось доказать, что оно всюду плотно в .
Доказательство. Пусть — любое непустое открытое подмножество пространства . Возьмём любую точку . Так как открыто, существует такое 0$» title=»$\varepsilon>0$» />, что . Возьмём любое натуральное \frac 2<\varepsilon>$» title=»$n>\frac 2<\varepsilon>$» />. Так как всюду плотно в , найдётся точка . Так как множество содержит точку , то есть, не пусто, то при построении была выбрана точка . Имеем

поэтому , то есть, , поэтому всюду плотно в .

Источник

Сепарабельное пространство

Сепара́бельное пространство (от лат. separabilis — отделимый) — топологическое пространство, содержащее конечное или счётное всюду плотное множество.

Многие пространства, возникающие в математическом анализе и геометрии, являются сепарабельными. Сепарабельные пространства обладают некоторыми привлекательными для математиков свойствами вытекающих из возможности представить каждый элемент пространства как предел последовательности элементов из счётного множества, подобно тому как всякое вещественное число можно представить как предел последовательности из рациональных чисел.

Многие теоремы могут быть доказаны конструктивно только для сепарабельных пространств. Типичным примером такой теоремы является теорема Хана — Банаха, которая в случае сепарабельных пространств может быть доказана конструктивно, но в противном случае использует для доказательства аксиому выбора.

Свойства

Примеры

См. также

Полезное

Смотреть что такое «Сепарабельное пространство» в других словарях:

СЕПАРАБЕЛЬНОЕ ПРОСТРАНСТВО — топологическое пространство, обладающее счетной базой. Про такие пространства иногда говорят, что они удовлетворяют второй аксиоме счетности. М … Математическая энциклопедия

МЕТРИЧЕСКОЕ ПРОСТРАНСТВО — множество Xвместе с нек рой метрикойr на ном. Теоретико множественный подход к изучению фигур (пространств) основан на исследовании взаимного расположения составляющих их элементарных частей. Одной из фундаментальных характеристик взаимного… … Математическая энциклопедия

Локально стягиваемое пространство — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия

ПСЕВДОМЕТРИЧЕСКОЕ ПРОСТРАНСТВО — множество X, наделенное псевдометрикой. Каждое П. м. нормально и удовлетворяет первой аксиоме счетности. Вторая аксиома счетности выполняется в том и только в том случае, когда X сепарабельное пространство. М. И. Войцеховский … Математическая энциклопедия

БАНАХОВО ПРОСТРАНСТВО — В пространство, полное нормированное векторное пространство. Исходными для создания теории Б. п. послужили введенные (в 1904 18) Д. Гильбертом (D. Hilbert), М. Фреше (М. Frechet) и Ф. Рисом (F. Riesz) функциональные пространства. Именно в этих… … Математическая энциклопедия

ЯДЕРНОЕ ПРОСТРАНСТВО — локально выпуклое пространство, у к рого все линейные непрерывные отображения в каждое банахово пространство являются ядерными операторами. Понятие Я. п. возникло [1] при исследовании вопроса о том, для каких пространств справедливы аналоги… … Математическая энциклопедия

КОНСТРУКТИВНОЕ МЕТРИЧЕСКОЕ ПРОСТРАНСТВО — концепция метрич. пространства, используемая в конструктивной математике. Близкий смысл имеет также понятие рекурсивного метрического пространства. Список где некоторое множество конструктивных объектов (обычно слов в том или ином алфавите), р… … Математическая энциклопедия

Источник