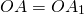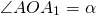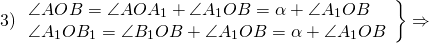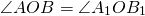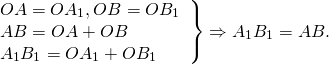Докажите что поворот является движением

Поворот

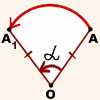
Отметим на плоскости точку O — центр поворота. Зададим угол α — угол поворота.

Поворот плоскости вокруг точки O на угол α — это отображение плоскости на себя, при котором каждая точка A отображается в такую точку A1, что

При этом точка O остаётся на месте (отображается сама в себя), а все остальные точки поворачиваются вокруг точки O в одном и том же направлении — либо по часовой стрелке, либо против часовой стрелки.

Поворот является движением

(то есть отображением плоскости на себя, сохраняющим расстояние).

Если точки A, O и B не лежат на одной прямой.

Пусть точка O — центр поворота, α — угол поворота. При повороте вокруг точки O на угол α против часовой стрелки точка A отобразится в точку A1, точка B — в точку B1.

Проведём отрезки AB и A1B1.

Рассмотрим треугольники AOB и A1OB1.

2) OB=OB1 (по определению поворота).

Следовательно, треугольники AOB и A1OB1 равны (по двум сторонам и углу между ними).

Из равенства треугольников следует равенство соответствующих сторон: AB=A1B1.

Если точки A, O и B лежат на одной прямой.

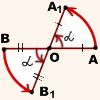
При повороте в направлении по часовой стрелке все рассуждения аналогичны.

Равенство A1B1=AB означает, что при повороте расстояние между точками сохраняется, а значит, поворот является движением.

Источник

Поворот

Урок 42. Геометрия 9 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Поворот»

Прежде чем приступить к изучению нового материала давайте повторим, что если каждой точке плоскости ставится в соответствие какая-то точка этой же плоскости, причем любая точка плоскости оказывается сопоставленной некоторой точке, тогда говорят, что дано отображение плоскости на себя.

Вспомним, что движение плоскости – это отображение плоскости на себя, сохраняющее расстояния.

Мы уже познакомились и повторили некоторые виды движения: такие как осевая симметрия, центральная симметрия, параллельный перенос.

Сегодня на уроке мы познакомимся с еще одним видом отображения плоскости на себя – поворотом.

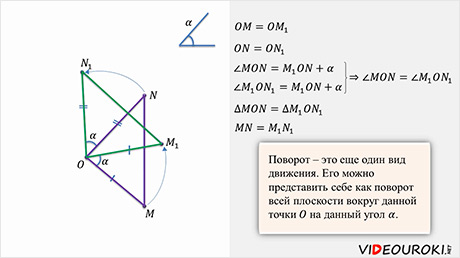
Давайте отметим на плоскости произвольную точку О, назовем ее центром поворота, и зададим угол α (назовем его углом поворота).

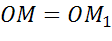
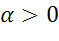
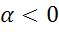
Поворотом плоскости вокруг точки О на угол α называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М₁, что и угол MOM₁=α. Заметим, что точка О остается на месте, то есть другими словами, отображается сама в себя, а все остальные точки поворачиваются вокруг точки О, причем, если , то против часовой стрелки, если , то по часовой стрелке

Иногда в литературе можно встретить следующее обозначение для поворота вокруг центра О и на угол α: .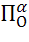

Теперь давайте попробуем определить, будет ли поворот движением? Для этого достаточно показать, что при повороте сохраняется расстояние между точками.

Пусть точка О – центр поворота, а угол α– угол поворота.

Рассмотрим случай, когда α>0, то есть поворачивать относительно точки О будем против часовой стрелки. Случай, когда α Оцените видеоурок

Источник

Презентация к уроку

Цели урока:

Содержание темы: урок по геометрии разработан для учащихся 9 класса.

Тип урока: урок изучения нового материала и промежуточного контроля усвоения учащимися пройденного на этом уроке и изученного ранее материала.

Организационные формы общения: коллективная, индивидуальная, фронтальная, в парах.

Оформление: мультимедийный проектор, экран, ноутбук, компьютерная презентация, сигнальные карточки.

Мотивационная беседа.

Без движения — жизнь только летаргический сон.
Жан Жак Руссо

I. Сообщение темы, целей и хода урока. (СЛАЙД 2)

— Ребята, Вы знаете какую важную роль имеет движение в жизни человека, общества, науки. Большую роль играет движение и в математике: преобразование графиков, отображение точек, фигур, плоскостей – всё это движение. На предыдущих уроках мы с Вами рассмотрели несколько видов движения. Сегодня мы познакомимся ещё с одним видом движения: поворотом. Тема урока: поворот.

И наш урок тоже является примером движения, только движения не с физической точки зрения, а движением в умственном развитии, познании нового и приобретения новых знаний. В течение всего урока Вы будете выполнять различные задачи, тесты. Поэтому будьте активны, продвигайтесь в своих знаниях вперёд на протяжении всего урока и улучшайте свои результаты от одного этапа к другому!

В течение всего урока, как мою речь, так и вашу будет сопровождать презентация, которая поможет проверить правильность выполнения Вами домашней работы, предложенных тестов и самостоятельно решённых задач.

II. Проверка домашнего задания.

С помощью СЛАЙДОВ 3-5 проверить решение № 1165.

III. Актуализация опорных знаний.

После выполнения теста ребята обмениваются тетрадями и выполняют взаимопроверку.

IV. Изучение нового материала. (обогащение знаний)

(СЛАЙД 14) Отметим на плоскости точку О (неподвижная точка), и зададим угол a – угол поворота. Поворотом плоскости вокруг точки О на угол a называется отображение плоскости на себя, при котором каждая точка M отображается в такую точку M₁, что OM =OM₁ и угол MOM₁ = a.

(СЛАЙД 15) При этом точка O остаётся на месте, т.е. отображается сама в себя, а все остальные точки поворачиваются вокруг точки O в одном и том же направлении на угол a по часовой стрелки или против часовой стрелки.

(СЛАЙД 17) Если поворот выполняется по часовой стрелке, то угол поворота a считается отрицательным. Если поворот выполняется против часовой стрелки, то угол поворота – положительный.

— Ребята, давайте вспомним понятие движения. Как Вы думаете, является ли поворот движением? (высказывают предположения)

— Поворот – является движением, т.е. отображением плоскости на себя. Докажем это.

(СЛАЙД 18 или СЛАЙД 19)

(Доказательство может выполнить сильный ученик по СЛАЙДУ 18. В этом случае можно сразу после доказательства перейти к СЛАЙДУ 20. Доказательство может выполнить учитель вместе с классом по СЛАЙДУ 19, на котором отображаются этапы доказательства.)

V. Закрепление изученного материала.

— Какие инструменты нам понадобятся для того, чтобы выполнить поворот? (линейка, циркуль, транспортир)

— Ребята, что сначала нужно отметить? (точку M и центр поворота – точку O)

— Как задаём центр поворота? Отмечаем в определённом месте? (нет, произвольно)

— Как будем выполнять поворот по часовой или против часовой стрелки? Почему? (против, т.к. угол положительный)

— Как найти на второй стороне угла точку M₁? (с помощью циркуля отложить отрезок OM₁=OM)

— Рассмотрим, как выполняется поворот отрезка в зависимости от расположения центра поворота.

— Рассмотрим случай, когда центр поворота лежит вне отрезка. Решим № 1166 (а). (Если класс сильный, то можно вместе с детьми составить план решения задачи, дать задание решить № 1166 (а) самостоятельно. Решение проверить с помощью СЛАЙДА 21. Если ребята затрудняются с выполнением задания, то решать коллективно, опираясь на СЛАЙД 21)

Работа в парах.

— Какая точка является центром поворота? Что можно о ней сказать? (это один из концов отрезка – точка А, она будет неподвижной, оставаться на месте)

— Как будем выполнять поворот по часовой стрелки или против часовой? (по часовой, т.к. угол отрицательный)

— Составьте план решения задачи.

Задание выполняют по парам. Проверяют решение с помощью СЛАЙДА 22.

Индивидуальная работа.

Задание. Построить фигуру, в которую переходит отрезок AB при повороте на угол – 100 o вокруг точки О – середины отрезка AB.

— Составьте план решения задачи. Задание выполняют самостоятельно, решение проверяем с помощью СЛАЙДА 23.

— Сегодня на уроке мы рассмотрели поворот отрезка в зависимости от расположения центра поворота. На следующих уроках мы рассмотрим повороты других фигур. (продемонстрировать СЛАЙДЫ 24-25)

VI. Проверка усвоения изученного материала.

Тест №2. (СЛАЙДЫ 26-30)

VII. Подведение итога урока. (рефлексия)

— Ребята, давайте выделим тех, кто был лучшим на каждом этапе. (подводится итог, выставляются оценки)

— Поднимите руки, кому понравился урок. Отметьте, что интересного было на уроке?

Источник

Поворот

Отметим на плоскости точку О (центр поворота) и зададим угол а (угол поворота). Поворотом плоскости вокруг точки О на угол α называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М₁, что ОМ = ОМ₁ и угол МОМ₁ равен α (рис. 330). При этом точка О остаётся на месте, т. е. отображается сама в себя, а все остальные точки поворачиваются вокруг точки О в одном и том же направлении — по часовой стрелке или против часовой стрелки. На рисунке 330 изображён поворот против часовой стрелки.

Поворот является движением, т. е. отображением плоскости на себя, сохраняющим расстояния.

Докажем это. Пусть О — центр поворота, α — угол поворота против часовой стрелки (случай поворота по часовой стрелке рассматривается аналогично). Допустим, что при этом повороте точки М и N отображаются в точки М₁ и N₁ (рис. 331). Треугольники OMN и ОМ₁N₁ равны по двум сторонам и углу между ними: ОМ = ОМ₁, ON = ON₁ и ∠MON = ∠M₁ON₁ (для случая, изображённого на рисунке 331, каждый из этих углов равен сумме угла α и угла M₁ON). Из равенства этих треугольников следует, что MN = M₁N₁, т. е. расстояние между точками М и N равно расстоянию между точками М, и N, (случай, когда точки О, М и N расположены на одной прямой, рассмотрите самостоятельно). Итак, поворот сохраняет расстояния между точками и поэтому представляет собой движение. Это движение можно представить себе как поворот всей плоскости вокруг данной точки О на данный угол α.

Источник

Докажите что поворот является движением

Это занятие будет посвящено теме «Поворот». Мы решим несколько задач на упомянутую тему, но для начала повторим понятие движения. После чего рассмотрим один из видов движения – поворот, перечислим его свойства и особенности. Решим вместе с преподавателем задачи на эту тему.

Если у вас возникнет сложность в понимании тему, рекомендуем посмотреть урок «Связь числа и геометрии. Часть 1. Измерения в геометрии. Свойства фигур»

Тема: Движение

Урок: Поворот как разновидность движения

Движение – отображение плоскости на себя, при котором расстояния между точками плоскости сохраняются.

Примеры движения: осевая симметрия, центральная симметрия, параллельный перенос.

Свойства движения: отрезок переходит в отрезок, угол переходит в равный ему угол, окружность переходит в окружность того же радиуса и т. п.

Пусть имеется некоторая выделенная точка О плоскости. Кроме того, рассмотрим произвольную точку М той же плоскости. Поворотом (обозначение – ) относительно точки О, называемой центром поворота на Ðα (угол поворота) называется такое отображение плоскости на себя, при котором любая точка М плоскости переходит в такую точку М₁ той же плоскости, что ОМ = ОМ₁ и, кроме того, ÐМОМ₁ = α (Рис. 1).

Докажем, что поворот является движением.

Доказательство (Рис. 2).

Рассмотрим точки М и N плоскости, переходящие при повороте соответственно в точки М₁ и N₁ той же плоскости.

Рассмотрим треугольники ОМN и ОМ₁N₁. В этих треугольниках ОМ = ОМ₁ и ОN = ОN₁. ÐМОN = α – ÐМОN₁; ÐМ₁ОN₁ = α – ÐМОN₁, следовательно, ÐМОN = ÐМ₁ОN₁. Таким образом, указанные треугольники равны по двум сторонам и углу между ними. Отсюда вытекает равенство отрезков МN = М₁N₁. Поскольку точки М и N выбирались нами произвольно, можно утверждать, что при повороте длины отрезков сохраняются.

Нам необходимо научиться использовать рассмотренный тип движения.

Задача (аналогичная № 1167 из учебника Атанасян, см. список литературы)

Постройте треугольник, который получается из данного треугольника ABC поворотом вокруг точки А на угол 60° против часовой стрелки ( ∆АВС).

При повороте точка А перейдет в саму себя. Точки В и С перейдут в точки В₁ и С₁ соответственно. Углы треугольника и длины его сторон, в соответствии с общими свойствами движения, сохранятся (все обозначения сторон и углов даны на Рис. 3).

Построения при повороте крайне простые: при помощи циркуля построить дугу окружности радиусом, равным длине стороны треугольника (АС или АВ), с центром в точке А, далее при помощи транспортира отложить на дуге угол 60° и отметить точку-образ (В₁ или С₁). Соединив полученные точки-образы отрезками, можно получить искомый треугольник А₁В₁С₁, являющийся образом треугольника АВС (∆АВС = ∆А₁В₁С₁).

Задача (Атанасян, № 1168).

Точка О является точкой пересечения биссектрис равностороннего треугольника ABC. Докажите, что при повороте вокруг точки О на угол 120° треугольник ABC отображается на себя.

Сделаем рисунок (Рис. 4).

Задача. Дана прямая, на которой заданы точка О₁ и точка О₂ и даны точки А и В, лежащие по разные стороны от этой прямой. Причем имеют место равенства расстояний: О₁А = О₁В, О₂А = О₂В.

Доказать, что точки А и В симметричны относительно указанной прямой.

Построим окружность радиусом О₁А с центром в точке О₁ и окружность радиусом О₂А с центром в точке О₂.

Рассмотрим некоторую осевую симметрию с осью О₁О₂. При таком отображении полуокружности, расположенные в верхней полуплоскости, перейдут в соответствующие полуокружности, расположенные в нижней полуплоскости относительно оси симметрии. При этом точка пересечения «верхних» полуокружностей – точка А – перейдет в точку пересечения «нижних» полуокружностей – точку В. То есть точка В симметрична точке А относительно рассматриваемой прямой. Задача решена.

В заключение разберем еще один простое применение понятий симметрии.

Дан параллелограмм ABCD.

Доказать, что точка пересечения его диагоналей является его центром симметрии.

Напоминание: фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией.

На рисунке точка О – точка пересечения диагоналей параллелограмма. В силу свойств параллелограмма AО = ОC и BО = ОD, а также любой отрезок, концы которого лежат на противоположных сторонах и проходящий через точку О (например, отрезок MN на Рис. 6), делится в этой точке пополам. Это означает, что при осуществлении центральной симметрии относительно центра, расположенного в точке О, все точки, принадлежащие сторонам, перейдут в точки, также принадлежащие сторонам. Таким образом, параллелограмм перейдет сам в себя, т. е. точка О – центр симметрии.

Подведем итоги: на данном уроке мы ввели в рассмотрение новый вид отображения плоскости на себя – поворот, доказали, что он является движением и решили ряд задач, которые помогут лучше понять изучаемую тему.

Список рекомендованной литературы

1. Атанасян Л. С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010.

2. Фарков А. В. Тесты по геометрии: 9 класс. К учебнику Л. С. Атанасяна и др. – М.: Экзамен, 2010.

3. Погорелов А. В. Геометрия, уч. для 7–11 кл. общеобр. учрежд. – М.: Просвещение, 1995.

Рекомендованные ссылки на интернет-ресурсы

1. Российский общеобразовательный портал (Источник).

2. Фестиваль педагогических идей «Открытый урок» (Источник).

Рекомендованное домашнее задание

1. Атанасян (см. список литературы), стр. 293, § 1, пункты 116, 117.

Источник