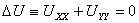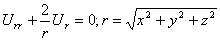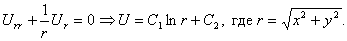Докажите что при конформном отображении областей гармонические функции переходят в гармонические
Конформное отображение
Понятие конформных отображений, их осуществление через элементарные функции. Основные принципы теории конформных отображений об отображении одной заданной области на другую. Принципы непрерывности и симметрии. Конформность дифференцируемого отображения.
| Рубрика | Математика |
| Вид | курсовая работа |
| Язык | русский |
| Дата добавления | 11.10.2011 |
| Размер файла | 2,5 M |
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
Размещено на http://www.allbest.ru/
1. Понятие конформного отображения
Основные принципы теории конформных отображений о отображении одной области на другую
1) существует аналитическая в функция конформно отображающая на единичный круг
2) эту функцию можно выбрать так, что будут выполнятся условия
где заданные точки, заданное действительное число. При этом функция условиями (1) определяются однозначно.
Две односвязные области, каждая из которых имеет не менее двух граничных точек, можно конформно отобразить одну на другую. Важным теоретическим положением, характеризующим поведение конформного отображения вблизи границы области, является следующий принцип соответствия границ.
Для доказательства теоремы достаточно показать, что
2) для каждой точки не существует точки такой, что т.е. функция не принимает значения ни при каком
Теорема 3 (принцип сохранения области) Если функция аналитична в области и не является постоянной, то образ области также является областью.
Для доказательства теоремы требуется показать, что множество линейно связанное и открытое. Так как отображение в силу аналитичности является непрерывным отображением, то образ любого линейно связанного множества при этом отображении является линейно связанным множеством. Следовательно, линейно связанное множество.
конформное отображение функция
2. Элементарные функции
Теория конформных отображений подчинена решению двух основных задач:
1) найти образ области при заданном отображении;
2) найти конформное отображение одной заданной области на другую.
В теории конформных отображений нет универсального метода, обеспечивающего решение какой-либо из двух задач. Нет общего алгоритма, позволяющего найти образ заданной области при заданном отображении, а тем более нет алгоритма построения конформного отображения из одной области в другую. Ситуация здесь та же, что и во многих других разделах математического анализа: решение конкретной задачи можно найти, хорошо зная конформные отображения, осуществимые элементарными аналитическими функциями, а также конформные отображения типовых областей. Решение конкретной задачи сводят в решению одной из стандартных задач.
Перейдем к рассмотрению конформных отображений, осуществляемых основными элементарными функциями.
Определение 3. Отображение, осуществимое линейной функцией
аналитической в комплексной плоскости, называют линейным.
Линейная функция обладает следующими свойствами.
Доказательство: Добавим к (3) условие
2) Для линейной функции существует обратная функция:
которая также является линейной функцией
3) Во всех точках плоскости функция является дифференцируемой, причем ее производная вычисляется по формуле
Для доказательства дифференцируемости функции найдем действительную и мнимую части линейной функции, покажем, что эти функции дифференцируемы, как функции 2-х действительных переменных, и выполняются условия К.-Р.
+, или, что тоже самое,
Функции и являются многочленами первого порядка, а, следовательно, они дифференцируемы любое число раз как функции двух переменных.
Найдем их частные производные:
отсюда следует, что
Учитывая свойство 3) разложим линейную функцию в ряд Тейлора в любом
Отображение с помощью линейной функции:
Рассмотрим сначала частные специальные случаи линейных функций:
Любая линейная функция может быть представлена в виде композиции трех линейных функций частного вида: Отсюда заключаем, что линейное отображение общего вида (3) можно осуществить путем последовательного применения:
1) Поворота около начала координат на угол ;
2) Преобразования подобия с центром подобия в точке и коэффициентом подобия ;
3) Параллельного переноса на вектор, изображающий комплексное число
Линейное отображение будет определено однозначно и в том случае, когда в некоторой точке заданы значения функции и значения ее производной (эта производная постоянна и на самом деле не зависит от точки ). При этих условиях отображение можно записать в виде
При этом под углом между кривыми в точке. понимается угол между образами этих кривых при отображении в точке
Используя эти определения получаем cвойства дробно-линейного отображения:
1) Дробно-линейная функция представима в виде:
Находим производную функцию в точке :
Находим производную функции в точке :
Итак, отображение представляет собой конформное отображение во всей расширенной плоскости.
2) Круговое свойство дробно-линейного отображения: произвольное дробно-линейное отображение переводит окружность комплексной плоскости в некоторую окружность расширенной комплексной плоскости (под окружностью в понимается либо обычная окружность в центром в некоторой конечной точке и конечного радиуса, либо прямая).
Из этого представления видно, что дробно-линейное отображение является композицией трех отображений:
Заметим, что уравнение любой окружности в (т.е. любой окружности в и любой прямой в ) можно записать в виде
Мы пришли к уравнению того же вида, что и уравнение
3) Сохранение симметрии при дробно-линейном отображении.
4) Инвариант дробно-линейного отображения
Действительно, так как
Определим двойное отношение:
Замечание 3. формула (5) остается справедливой при построении дробно-линейного отображения, переводящего заданные точки в заданные. Если среди встречается (или ), т.е. допускается бесконечность, как в левой, так и в правой части, то этом случае числитель и знаменатель дроби, где встречается бесконечность, следует заменить 1.
Свойства степенных функций:
5) Образом области однолистности при отображении является вся плоскость с разрезом вдоль положительной части действительной оси.
Однако если в качестве геометрического образа функции рассматривать более сложное многообразие, чем обычная комплексная плоскость, можно сохранить взаимную однозначность отображения.
Определение 7. Функция вида:
называется показательной функцией.
Свойства показательных функций:
Так как то отображение, осуществимое показательной функцией, будет конформным во всей комплексной плоскости.
2) Функция имеет отличную от нуля производную во всех точках плоскости
Тригонометрические функции комплексной переменной
Определение 8. Из формулы Эйлера для всех действительных имеем
Эти формулы можно использовать для голоморфного продолжения косинуса и синуса в комплексную плоскость, положив по определению для любого :
Свойства тригонометрических функций комплексного переменного:
3) Для любых справедливо:
4) Функции и имеют лишь действительные нули, а именно:
6) Тригонометрические функции комплексного переменного тесно связаны с гиперболическими, которые для любого определяются формулами
Эта связь выражается соотношениями
7) Пользуясь свойствами 4) и 7) получим
Величины и являются неограниченными, а именно вдоль мнимой оси, аналогично при
8) Тангенс и котангенс для комплексных значений аргумента определяются формулами
Рассмотрим примеры конформных отображений осуществимых основными элементарными функциями:
Для этого последовательно выполним следующие отображения:
Таким образом, получаем искомое отображение (Рис. 8)
2) Найти линейную функцию, отображающую треугольник с вершинами на треугольник с вершинами.
Тогда вершины одного треугольника переходят в вершины другого треугольника соответственно:
ЃЛЃЛ функция принимает вид
Для решения поставленной задачи установим следующее соответствие граничных точек данных областей (рис. 10):
Последний коэффициент определяется из условия (2):
4) Отобразить конформно множество на множество
Нужно найти функцию
Найдем отображение осуществимое множествами:
Нужно найти функцию
1) Нужно повернуть на
3) Сместить на 1 вправо:
Область принимает вид (Рис. 12):
Подставим крайние точки области в функцию :
Для нахождения и в заданную функцию подставим и выделим действительную и мнимую части:
поскольку комплексные числа и являются комплексно сопряженными, а значит, имеют равные модули.
Размещено на Allbest.ru
Подобные документы
Понятие конформного отображения и его основные свойства. Основные принципы конформных отображений функций комплексного переменного, их гидродинамические аналогии и интерпретации. Применение метода конформных отображений в механике сплошных сред.
дипломная работа [2,6 M], добавлен 26.08.2014
Основные особенности решения гидродинамических задач методом конформных отображений. Сущность понятия «конформное отображение». Анализ задачи об обтекании твердого тела потоком жидкости. Знакомство с интегрированными функциями комплексного переменного.
контрольная работа [1,1 M], добавлен 22.03.2013
Комплексная форма записи простейших преобразований плоскости. Определение, основные свойства комплексного отображения. Использование простейших рациональных функций для выполнения некоторых конформных отображений. Построение профилей Жуковского-Чаплыгина.
курсовая работа [2,0 M], добавлен 03.12.2014
Непрерывные отображения топологических пространств. Связность топологических пространств. Компактность топологических пространств. Связность непрерывных отображений. Замкнутые отображения. Связь связности и послойной связности.
курсовая работа [140,7 K], добавлен 08.08.2007
Сущность конформного отображения 1 и 2 рода, аналитической функции в заданной области. Геометрический смысл аргумента и модуля производной функции. Величина коэффициента растяжения в точке. Сохранение функции отличной от нуля по величине и напряжению.
презентация [83,3 K], добавлен 17.09.2013
Декартова система координат. Построение композиции отображений. Проверка полноты системы функций. Построение логической схемы однотактного триггера на заданном элементе памяти с использованием канонического метода структурного синтеза конечных автоматов.
контрольная работа [225,5 K], добавлен 18.02.2015
Исторический процесс развития взглядов на существо математики как науки, основные этапы формирования аксиоматического метода. Теории групп, множеств, отображений и конгруэнтности (равенства) отрезков. Основные аксиоматические теоремы и их доказательства.
курсовая работа [26,2 K], добавлен 24.05.2009
Презентация была опубликована 9 лет назад пользователемifoshki.narod.ru
Похожие презентации
Презентация на тему: » Овчинцев Евгений ИФО 3-2 Применение метода конформных преобразований к уравнениям математической физики.» — Транскрипт:
1 Овчинцев Евгений ИФО 3-2 Применение метода конформных преобразований к уравнениям математической физики
2 Введение Функция называется гармонической, если : 1. Существуют частные производные до второго порядка включительно. 2. Все они непрерывны. 3. Она удовлетворяет уравнению Лапласа :
3 Методы функции комплексного переменного Если комплексная функция имеет первую производную в области G 1. Она бесконечное число раз дифференцируема. 2. Все эти производные непрерывны и
5 О сохранении гармоничности функции при конформном отображении. Пусть – некоторая гармоническая функция, заданная внутри области.
6 О сохранении гармоничности функции при конформном отображении. Тогда частные производные от функции : Следовательно, вторые частные производные от нее же :
8 О сохранении гармоничности функции при конформном отображении. Из получившихся соотношений следует : Т. к. Т. е. – гармоническая функция в.
9 Задача Дирихле Найти функцию, удовлетворяющую условиям : где – заданная непрерывная функция на границе области.
10 Задача Дирихле Теорема : « Решение задачи Дирихле существует и притом единственно ».
11 Практическая задача Труба радиуса r помещена на заданной глубине. Найти установившееся распределение температуры в почве, если на поверхности земли она равна нулю, а температура трубы ( рис.1).
12 Практическая задача – температура земли в точке. – гармоническая функция. Для нее должно выполняется уравнение и она должна удовлетворять граничным условиям
14 Практическая задача Отобразим область G конформно на круговое кольцо : ( рис.2) В кольце получили задачу Дирихле :
16 Решение практической задачи Найдем на оси две точки ( рис.3) такие, что они являются симметричными и для оси и для окружности одновременно.
17 Решение практической задачи Рассмотрим дробно-линейное отображение : Подставим в него : Докажем, что эта функция отображает область на круговое кольцо :
18 Решение практической задачи – ось. Пусть. Тогда То есть, и, значит, образом оси является окружность.
19 Решение практической задачи Найдем образ окружности. Ее образом будет окружность с центром в точке. Таким образом область отображается на круговое кольцо. Найдем. Образом точки будет точка, лежащая на окружности. Следовательно :
20 Решение практической задачи Решение нашей основной задачи имеет вид : Перейдя к переменным и, получим : где
21 Рассмотрим конкретный пример Пусть a=2, h=4, а T=10. Тогда А график этой функции имеет вид :
Лекция 7. Гармонические функции и их свойства
Рассмотрим уравнение Лапласа на плоскости
Уравнение (33) при переходе к полярным координатам преобразуется к виду
Рис 14 Рис 14.1
Если в пространстве перейти к сферическим координатам
то уравнение (34) примет вид
Решение U=U(r), обладающее сферической симметрией, будет определяться из обыкновенного дифференциального уравнения
Это уравнение получится, если подставить искомую функцию в уравнение Лапласа (34*), записанное в сферических координатах. Интегрируя это уравнение, находим
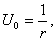
которую часто называют фундаментальным решением уравнения Лапласа в пространстве. Функция U0 является гармонической всюду в пространстве, кроме начала координат 0.
Аналогично, полагая U=U(r) и пользуясь уравнением Лапласа в цилиндрических или полярных координатах, найдем решения, обладающие цилиндрической или круговой симметрией:
Выбирая С1=-1 и С2=0, будем иметь функцию
Аналогично, если рассмотреть поле, создаваемое заряженной прямой, то потенциал такого поля будет равен
Более сложные примеры будут рассмотрены далее, а сейчас изучим свойства гармонических функций.
Теорема о среднем. Пусть функция U=U(x,y) гармоническая в некотором круге D радиуса R с центром (хo,уo) и непрерывная в соответствующем замкнутом круге Тогда значение этой функции в центре круга равно ее среднему значению на окружности Г, ограничивающей данный круг, то есть
При доказательстве этой теоремы применим интегральную формулу Пуассона для круга, которая будет доказана позже в лекции 10. Она имеет вид (см. рис. 15)
Если в этой формуле положить ρ=0, то получится формула (35).
Теорему о среднем можно представить и в другой форме. Для этого запишем формулу (35) для произвольного круга радиуса r, где 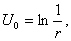
Умножив обе части равенства (36) на rdr и проинтегрировав по r в пределах от 0 до R, получим:
В правой части формулы (37) записано среднее значение гармонической функции U(x,y) в круге радиуса R.
Имеет место и обратная теорема: если в некоторой области D функция U=U(x,y) непрерывная и для каждой точки выполняется теорема о среднем в любом сколь угодно малом круге с центром в точке (хо, уо), то эта функция гармоническая в D. Из формулы (37) получается:
Неравенство (38) доказывается совсем просто, если воспользоваться известным неравенством Коши-Буняковского:
Применим это неравенство к формуле (37):
Что и требовалось доказать.
Гармонические функции, помимио вышеуказанных свойств, обладают и многими другими свойствами. Приведем еще два из них.
Неравенство Харнака. Пусть функция гармоническая в некотором круге D радиуса R c центром (xo, уo) и непрерывная в соответствующем круге Тогда при любом она удовлетворяет неравенству
Из неравенства Харнака следует теорема Лиувилля.
Теорема Лиувилля. Гармоническая на всей плоскости функция U=U(x, у) не может быть ограниченной сверху или снизу, если она не постоянная.
Воспользуемся неравенством Харнака
Если функция U(x, у) гармоническая во всей плоскости то, фиксировав произвольное и неограниченно увеличивая R мы получим
то есть Теорема Лиувилля доказана.
Замечание. Гармонические функции в пространстве обладают аналогичными свойсвами. Приведем формулировку одного из них.
а) ее среднему значению на сфере Г, ограничивающей данный шар, то есть
б) ее среднему значению в шаре D, то есть
СОДЕРЖАНИЕ
Этимология термина «гармонический»
Примеры
Примеры гармонических функций двух переменных:
Наконец, примеры гармонических функций от n переменных:
Замечания
Связь с теорией сложных функций
Хотя указанное выше соответствие с голоморфными функциями справедливо только для функций двух действительных переменных, гармонические функции от n переменных по-прежнему обладают рядом свойств, типичных для голоморфных функций. Они (настоящие) аналитические; у них есть принцип максимума и принцип среднего значения; для них справедлива теорема об устранении особенностей, а также теорема Лиувилля по аналогии с соответствующими теоремами теории комплексных функций.
Свойства гармонических функций
Некоторые важные свойства гармонических функций можно вывести из уравнения Лапласа.
Теорема регулярности для гармонических функций
Принцип максимума
Свойство среднего значения
И наоборот, все локально интегрируемые функции, удовлетворяющие свойству (объемного) среднего значения, являются как бесконечно дифференцируемыми, так и гармоническими.
допускает простое явное решение w r, s класса C 1,1 с компактным носителем в B (0, r ). Таким образом, если u гармоничен в Ω
Неравенство Гарнака
Устранение особенностей
тогда f продолжается до гармонической функции на Ω (сравните теорему Римана для функций комплексного переменного).
Теорема Лиувилля
Эдвард Нельсон дал особенно краткое доказательство этой теоремы для случая ограниченных функций, используя свойство среднего значения, упомянутое выше:
Учитывая две точки, выберите два шара с указанными точками в качестве центров и одинакового радиуса. Если радиус достаточно велик, два шара будут совпадать, за исключением сколь угодно малой части их объема. Поскольку f ограничено, его средние по двум шарам произвольно близки, и поэтому f принимает одинаковое значение в любых двух точках.
По свойству усреднения и монотонности интеграла имеем
Обобщения
Слабо гармоническая функция
Функция (или, в более общем смысле, распределение ) является слабо гармонической, если она удовлетворяет уравнению Лапласа
Гармонические функции на многообразиях
Гармонические функции могут быть определены на произвольном римановом многообразии с помощью оператора Лапласа – Бельтрами Δ. В этом контексте функция называется гармонической, если
Многие свойства гармонических функций на областях в евклидовом пространстве переносятся на эту более общую установку, включая теорему о среднем значении (по геодезическим шарам), принцип максимума и неравенство Гарнака. За исключением теоремы о среднем значении, это простые следствия соответствующих результатов для общих линейных эллиптических уравнений в частных производных второго порядка.
Субгармонические функции
Гармонические формы
Гармонические отображения между многообразиями
Гармонические функции
Связь с аналитическими функциями. Аналитические функции тесно связаны с гармоническими функциями от двух переменных, т. е. с решениями двумерного уравнения Лапласа
В самом деле, дифференцируя первое из условий аналитичности



Из свойств аналитических функций можно выводить соответствующие свойства функций гармонических (при желании можно поступать и наоборот). Так, мы можем утверждать, что каждая гармоническая функция бесконечно дифференцируема. Из формулы (19) предыдущего параграфа отделением действительных частей мы получаем теорему о среднем для гармонических функций:

Эта теорема является одним из основополагающих фактов теории гармонических функций. Из нее, в частности, получается важный принцип экстремума: непостоянная гармоническая в области D функция не может достигать внутри D ни максимума, ни минимума.


Возникает естественная задача восстановления гармонической в области функции по ее граничным значениям. Эта задача является основной в теории гармонических функций и ее приложениях и называется задачей Дирихле. Вот как она формулируется:
Приведенное выше рассуждение показывает, что задача Дирихле не может иметь двух различных решений, т. е. доказывает единственность решения этой задачи. Более тонким и сложно доказываемым фактом является существование решения задачи Дирихле. Впрочем, для ряда простейших областей существование решения можно доказать прямой конструкцией.

и, следовательно,воспользуемся теоремой
Теперь мы вычтем это равенство из предыдущего, предварительно подсчитав, что




Преобразованием формулы Коши (4), похожим на описанное, можно получить также интеграл Шварца, который восстанавливает аналитическую в единичном круге функцию f(z) по граничным значениям ее действительной части:
эта задача, очевидно, решается с точностью до мнимой постоянной.


В частности, гармоничность сохраняется при конформных отображениях, которые представляют собой взаимно однозначные аналитические преобразования.
Связь теории гармонических функций с теорией конформных отображений проявляется также в связи соответствующих граничных задач. Основной граничной задачей теории конформных отображений служит следующая задача Римана:

Остается вернуться к переменной г и воспользоваться сохранением гармоничности при конформных отображениях; мы получим искомое решение:

отображение f переводит в центр круга w = 0 (рис. 19).
В ней функция f должна иметь нуль, и притом первого порядка, ибо в окрестности нулей высшего порядка аналитическая функция не взаимно однозначна (она имеет там характер степени). Поэтому в окрестности z0 функция f должна иметь тейлоровское разложение вида


функции аналитичен в D, а значит, его действительная часть, т. е. функция
должна быть гармонической в D.
Теперь уже нетрудно понять замысел проведенных построений: ведь если f отображает D на единичный круг, то должен равняться 1 на границе D, а значит, еще не зная самого конформного отображения, мы знаем граничные значения функции (9), они равны
и определяются геометрической формой границы области и выбранной точкой z0 (рис. 19). Чтобы найти искомое конформное отображение, нужно, следовательно, выполнить следующие операции: 1) по известным граничным значениям (1СН построить гармоническую в D
функцию и(z) (задача Дирихле), 2) найти функцию v(z), гармонически сопряженную с и (интегрирование). Теперь мы знаем функцию
откуда искомое отображение находится по формуле
Хочется обратить внимание на некоторые тонкости, связанные с построенным решением. Из конструкции видно, что функция f аналитична в D и что на границе D ее модуль равен 1. Однако остается еще доказать, что эта функция взаимно однозначно отображает D на единичный круг. Это можно сделать прямой (но отнюдь не простой) проверкой. Если же у нас есть уверенность, что наша задача разрешима (т. е. мы умеем доказывать теорему существования конформного отображения D на круг), то такая проверка излишня — проведенные выше рассуждения показывают, что если искомое отображение есть, то оно непременно восстанавливается по формуле (11).