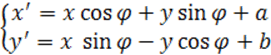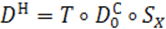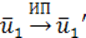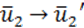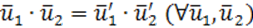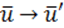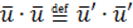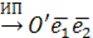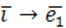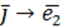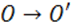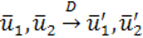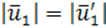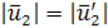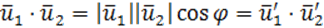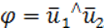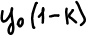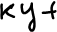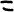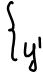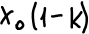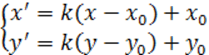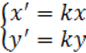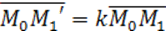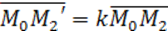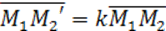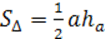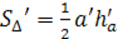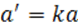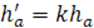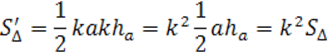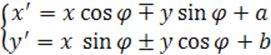Докажите что при ортогональном преобразовании сохраняется расстояние между точками

Т: 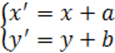– перенос плоскости на вектор <a;b>

Утверждение.Преобразование D C можно представить в виде композиции D C ₀ и Т, т.е. поворота плоскости вокруг начала координат на угол φ и переноса на вектор <a;b>.

С другой стороны преобразование D C при ненулевом угле φ равносильно повороту плоскости вокруг т.М₀ (без переноса).

Рассмотрим несобственное движение.

D Н : (VVV)

Рассмотрим частный случай.

S_x: 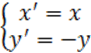симметрия относительно оси Ох

Любое D Н представимо в виде композиции

Изометрические преобразования (ИП). Связь с движениями.

Определение. АП, при котором сохраняется скалярное произведение векторов, называется изометрическим преобразованием.

Свойства изометрических преобразований

При ИП длины векторов сохраняются.

, .

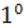
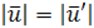
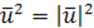
Следствие. При ИП сохраняется расстояние между точками.

совпадают со свойствами движения 1, 2, 3, 4, их доказательства так же совпадают.

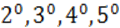
Теорема о связи ИП и Д.

Любое ИП – это движение, любое движение – это ИП.

Докажем, что это движение.

– ПДСК

в силу ИП

— ПДСК

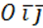
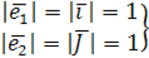
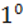
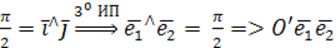
При ИП ПДСК→в ПДСК =>оно движение по определению.

2) пусть имеем D – произвольное движение.

Докажем что это ИП

т.к. при движении расстояние между точками сохраняется.

в силу движения

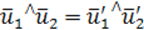
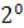
=>Движение есть ИП по определению.

Гомотетия. Преобразование подобия.

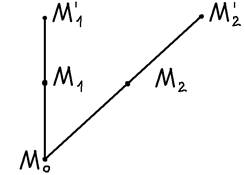
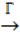
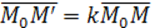
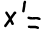
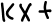
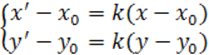
Определение. Гомотетией Г с центром в т. М₀ и коэффициентом kназывают АП плоскости, при котором т. М М’, так что , где М₀ – двойная точка.

Пусть M₀(x₀;y₀), M(x;y), M’(x’;y’)

=>Г:

Г. с центром в начале координат O и k

Г₀:

При гомотетии с коэффициентами k расстояние между точками изменяется в k раз.

с коэффициентом подобия kпо 2-м сторонам и углу между ними. Следовательно,

При гомотетии треугольники переходят в треугольники, подобные первоначальным.

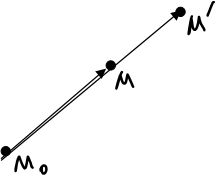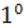
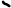
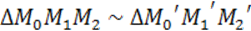
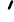
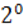
Доказательство: Признак подобия по трем сторонам.

При гомотетии углы между векторами сохраняются.

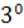
Доказательство: из 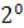свойства.

Δ→ в подобные Δ, а углы между соответствующими сторонами в подобных треугольниках равны.

При гомотетии с коэффициентом k площади Δ изменяются в k 2 раз.

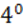
Преобразование подобия (ПП).

Определение. АП, при котором расстояние между любыми двумя точками изменяется в k раз, называется преобразованием подобия с коэффициентом k.

Свойства преобразования подобия

При ПП Δ ки → в Δ ки подобные первоначальным, с коэффициентом подобия k.

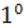
Доказательство: по определению.

При ПП углы между векторами сохраняются.

При ПП площади треугольников изменяются в k 2 раз.

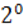
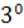
Свойства 2 и 3 доказываются абсолютно аналогично, как и для гомотетии

Замечание. При ПП и при Г площадь любой замкнутой фигуры изменяется в k 2 раз.

Теорема. Любое ПП с коэффициентом k можно представить в виде композиции гомотетии с коэффициентом k и некоторого движения.

Пусть имеем ПП Pс коэффициентом k, при этом преобразовании расстояние между точками изменяется в k раз.

Рассмотрим Г с коэффициентом и с центром в произвольной точке М₀.

При этой Г, в силу ее свойств, расстояние между двумя любыми точками изменяется в раз.

Если мы выполним композицию этих преобразований, то получим, что расстояние между точками не изменилось. Следовательно, композиция этих преобразований – это некоторое движение.

(*) ч.т.д.

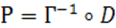
в формуле (*) центр гомотетии можно брать где угодно.

Рассмотрим гомотетию с центром в начале координат.

D:

Р(ПП): 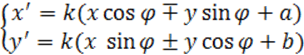(**) – формула любого ПП с коэффициентом k.

Источник

Описание файла

Просмотр PDF-файла онлайн

Текст 19 страницы из PDF

. Теорема доказана. 3 а м е ч а н и е. Так как при ортогональных преобразованиях расстояния сохраняются, то любая фигура на плоскости преобразуется в равную ей фигуру ‘).

Иными словами, ортогональное преобразование на плоскости можно рассматривать как движение этой плоскости. При движении ортогональная система координат переходит в ортогональную систему координат. Этим можно объяснить термин ортогональное преобразование. Ортогональные преобразования обладают следующими свойствами 2): 1′. Последовательное выполнение двух ортогональньгх преобразований есть ортогональное преобразование. 2′. Тождественное преобразование х’=х, у’=у является ортогональным преобразованием (для этого преобразования соотношения р3.43), очевидно, выполняются). 3′. Преобразование, обратное ортогональному, также является ортогональным.

Линейное преобразование в пространстве 92 прковрлзовлнив дкклртовых прямоугольных координгзт

— йзгйзз = О, 2 2 2 ам+ ага+ азз — — 1, аща„+ а,заря + азза„=О. (3.45) Ортогональное преобразование является аффинным, Справедливо следующее основное свойство ортогональных преобразований: при таких преобразованиях сохраняются расстояния между точками. Доказательство может быть проведено в полной аналогии с доказательством теоремы 3.4.

Ортогональные преобразования в пространстве обладают следующими свойствами. 1′. Последовательное выполнение ортогональньт преобразований является ортогональным преобразованием. 2′. Тождественное преобразование х’ = х, у ‘ = у, г’ = г — ортогональное преобразование. 3′. Преобразование, обратное ортогональному, также ортогональное. ф 4. Проективные преобразования Проективными преобразованиями на плоскости называются преобразования вида апх+а,ау+а|в, аг,х+аму+агз х’=, у’= 3! з тгзгу зз аззх ч иззу и азз (3.46) коэффициенты ау которых удовлетворяют условию ) ап а„а,з аг, агг агз

О. аз, а за азз При проективном преобразовании (3.46) плоскости особую роль играет прямая Е, определяемая уравнением аззх+ азау+ азз = О.

) Геометрически зто условие означает, что три прямые апх+а,ау+а,з — — О, онх+аз у+ам — — Оиамх+ а ту+ам — — вне пересекаются волноиточке(скт и. 54 2 ел 3) Для точек этой прямой знаменатели в выражениях для х ‘ и у ‘ (см. (3.46)) обращаются в нуль, и поэтому преобразование (3.46) не определено для точек этой прямой. ПРОЕКТИВНЫЕ ПРЕОБРАЗОВА!1ИЯ 3 4! Отметим, что проективное преобразование инвариантно относительно выбора декартовой системы координат, так как формулы перехода от одной декартовой системы координат к другой линейны и поэтому при переходе к новой системе координат вид преобразований (ЗАб) не меняется. Непосредственной проверкой можно убедиться, что последовательное проведение двух проективных преобразований является проективным преобразованием, тождественное преобразование и преобразование, обратное проективному, — также проективные преобразования.

При проективных преобразованиях точки, лежащие на прямой, переходят в точки, также лежащие на прямой. Основным инвариантом проективиого преобразования является так называемое сложное (ангармоническое) отношение (АВСР) любых четырех точек А, В, С и Р на прямой, которое определяется как частное двух простых отношении: (АВСР) = (АСВ): (АРВ). Инвариантность сложного отношения (АВСР) четырех точек прямой может быть обоснована так же, как и инвариантность простого отношения при аффинных преобразованиях.

— а24 — О, аз1Х+ иззу+ а313г+ азз= () азгх+ а42У+ аззг+ а44 — О не пересекаются в одной точке. Отметим, что проективное преобразование в пространстве не определено для точек плоскости, определяемой уравнением аз,х + а42У+ аз;за + а44 — — О.

94 ПРЕОВРЛЗОВЛНИЕ ДЕКАРТОВЫХ ПРЯМОУГОЛЬНЫХ КООРДИНАТ

ГЛ 3 Непосредственной проверкой можно убедиться, что последовательное проведение двух проективных преобразований, тождественное преобразование и преобразование, обратное проективному, — также проективные преобразования. При проективных преобразованиях точки, лежащие в одной плоскости, переходят в точки, также лежащие в одной плоскости, а точки, лежащие на прямой, переходят в точки, лежащие на прямой. Основным инвариантом проективного преобразования в пространстве является сложное отношение (АВСР) = (АСВ): ГАРВ) любых четырех точек А, В, С и Р на прямой.

ГЛАВА 4 УРАВНЕНИЕ ЛИНИИ НА ПЛОСКОСТИ. УРАВНЕНИЯ ПОВЕРХНОСТИ И ЛИНИИ В ПРОСТРАНСТВЕ В этой главе рассматривается один из важнейших вопросов аналитическая’ геометрии — вопрос об аналитическом представлении линии на плоскости и поверхности и линии в п)зостранстве при помощи уравнений, связывающих их координаты ). Обсуждаются простейшие задачи, связанные с таким аналитическим представлением, и приводится классификация плоских линий и поверхностей.

Доказывается, что порядок алгебраической линии (и соответственно поверхности) не зависит от выбора декартовой прямоугольной системы. ф 1. Уравнение линии на плоскости 1. Понятие об уравнении линии. Предположим, что на плоскости и нам заданы: 1) декартова прямоугольная система координат Оху и 2) некоторая линия т’.. Рассмотрим некоторое уравнение, связывающее две переменные величины х и у ) Ф(х, у) = О. (4.1) Определение. Уравнение(4.1) называется ура в н ен и ем л ин и и г’. (относительно заданной системы координат), если этому уравнению удовлетворяют координаты х и у любой точки, лежа- и(ей на линии ь, и не удовлетворяют координаты х и у ни одной точки, не лежащей на линии 1.. С точки зрения этого определения сама линия й представляет собой (в заданной системе координат) геометрическое место точек, координаты которых удав.гетворяют уравнению (4.1) Если (в заданной системе координат) рассматриваемое уравнение вида (4.1) является уравнением линии 1., то мы будем говорить, что это уравнение определяет линию ь.

) По поводу самого понятия линии (или соответственно поверхности) отсылаем читателя к гл, 11 вып, 1 настоящего курса ) Равенство Ф(х, д) = О, где Ф(х, у) — заданная функния двух переменных х и у, называется уравнением, если зто равенство справедливо не для всех пар вещественных чисел х, у. Равенство Ф(х, у) = О, справелливое для всех пар вещественных чисел х, у, называется тождеством. уРдвнш1ия новеРхности и линии 1гл 4 3 а м е ч а н и е.

Нетрудно указать такое уравнение вида (4.1), которое либо определяет геометрический образ, отличный от того, что мы привыкли понимать под термином «линия», либо вообще не определяет никакого геометрического образа. Так, уравнение хз+ у = 0 определяет на плоскости Оху лишь одну точку (0,0), а уравнение хз+ уз+ 1 = 0 вообще не определяет никакого геометрического образа.

Для того чтобы уравнение вида (4.1) определяло геометрический образ, отвечающий нашему привычному представлению о линии, следует, вообще говоря, подчинить функцию Ф(х, у) некоторым ограничениям (например требованию однозначной разрешимости функционального уравнения (4.1) относительно одной из переменных). Эти ограничения выясняются в курсе математического анализа (см. вып.

1, гл. 15, Э 2, п. 3). П р и м е р. Убедимся в том, что уравнение (х — а) +(у — Ь) =г (4.2) является уравнением окружности радиуса г > 0 с центром в точке Мо(а, Ь). В самом деле, точка М(х, у) лежит на указанной окружности тогда и только тогда, когда расстояние между точками М (х, у) и Мо(а, Ь) равно г, т.е.

Параметрическое представление линии. Для аналитического представления линии ь часто бывает удобно выражать переменные координаты х и у точек этой линии при помощи третьей вспомогательной переменной (или параметра) (: (4.4) х=ср(О, у=т)г(1), где функции тр(Г) и т)г(() предполагаются непрерывными по параметру ( (в некоторой области (() изменения этого параметра).

Исключение из двух уравнений (4.4) параметра ( приводит к рассмотренному выше уравнению вида (4.1) ‘). Параметрическое представление линии на плоскости естественно возникает, если эту линию рассматривать как путь, пройденный материальной точкой, непрерывно движущейся по определенному закону. В самом деле, если переменная ( представляет собой время, отсчитывае) Такое искяючение заведомо возможно. если котя бы одна из функции з = фа) изи у = дг(1) имеет обратную 1достато

ныс условия ддя этого см в и 4 Г) 2 гз 15 выи.

Источник

Линейные преобразования

Ортогональные преобразования.

Ортогональными называются такие преобразования плоскости, которые не меняют расстояния между любыми двумя точками, то есть преобразования \(f\) ортогональное, если для любых точек \(A\) и \(B\) выполнено \(|AB|=|f(A)f(B)|\).

Основными примерами ортогональных преобразований служат параллельный перенос, поворот и осевая симметрия.

Получим координатную запись ортогонального преобразования в декартовой прямоугольной системе координат \(O, \boldsymbol_<1>, \boldsymbol_<2>\). Обозначим через \(A\) и \(B\) концы базисных векторов: \(\boldsymbol_<1>=\overrightarrow\), \(\boldsymbol_<2>=\overrightarrow\) (рис. 12.1). При ортогональном преобразовании равнобедренный прямоугольный треугольник \(OAB\) перейдет в равный ему треугольник \(O^<*>A^<*>B^<*>\). Рассмотрим произвольную точку \(M(x, y)\). Она перейдет в точку \(M^<*>\) с координатами \((x^<*>, y^<*>)\). Нам надо выразить \((x^<*>, y^<*>)\) через \((x, y)\).

Рис. 12.1. Ортогональное преобразование.

По определению координат \(\overrightarrow=x\overrightarrow+y\overrightarrow\). Отсюда следует, что \(\overrightarrowM^<*>>=x\overrightarrowA^<*>>+y\overrightarrowB^<*>>\). Действительно, векторы \(\overrightarrowA^<*>>\) и \(\overrightarrowB^<*>>\) взаимно перпендикулярны и по длине равны 1, а потому компоненты \(\overrightarrowM^<*>>\) по этим векторам равны его скалярным проекциям на них. Эти проекции равны проекциям \(\overrightarrow\) на \(\boldsymbol_<1>, \boldsymbol_<2>\), что видно из равенства соответствующих треугольников. Теперь мы можем написать
$$
\overrightarrow>=\overrightarrow>+\overrightarrowM^<*>>=\overrightarrow>+x\overrightarrowA^<*>>+y\overrightarrowB^<*>>.\label
$$

Обозначим через \(\varphi\) угол между \(\overrightarrowA^<*>>\) и \(\boldsymbol_<1>\). Поскольку \(|\overrightarrowA^<*>>|=1\), координаты этого вектора в базисе \(\boldsymbol_<1>, \boldsymbol_<2>\) равны \((\cos \varphi, \sin \varphi)\). Тогда перпендикулярный вектор единичной длины \(\overrightarrowB^<*>>\) имеет координаты (\(\mp \sin,\ \pm \cos\)), причем верхние знаки берутся в том случае, когда пара векторов \(\overrightarrowA^<*>>\) и \(\overrightarrowB^<*>>\) ориентирована так же, как \(\boldsymbol_<1>, \boldsymbol_<2>\). Координаты точки \(O^<*>\) обозначим через \((c_<1>, c_<2>)\).

Теперь мы можем разложить все члены равенства \eqref по базису:
$$
\begin
& x^<*>=x \cos \varphi \mp y \sin \varphi+c_<1>,\\
& y^<*>=x \sin \varphi \pm y \cos \varphi+c_<2>.
\end\label
$$

Итак, мы доказали следующее утверждение.

Произвольное ортогональное преобразование в декартовой прямоугольной системе координат записывается формулами \eqref, где \(\varphi\) — угол, на который поворачивается первый базисный вектор, a \(c_<1>\) и \(c_<2>\) — координаты образа начала координат. При этом выбираются верхние знаки, если образы базисных векторов ориентированы так же, как и сами эти векторы, и нижние знаки в противоположном случае.

Параллельный перенос на вектор с сопоставляет точке \(M\) с координатами \((x, y)\) в некоторой декартовой системе координат точку \(M^<*>\) с координатами
$$
x^<*>=x+c_<1>,\ y^<*>=y+c_<2>,\nonumber
$$
где \(c_<1>\) и \(c_<2>\) — координаты \(c\).

Напишем уравнения поворота плоскости на угол \(\varphi\) вокруг некоторой точки, приняв эту точку за начало декартовой прямоугольной системы координат. В этом случае \(O=O^<*>\) и, следовательно, \(c_<1>=c_<2>=0\). Должны быть выбраны верхние знаки. Итак
$$
x^<*>=x \cos<\varphi>-y \sin<\varphi>,\ y^<*>=x \sin<\varphi>+y \cos<\varphi>,\nonumber
$$

Рассмотрим осевую симметрию относительно некоторой прямой. Примем ось симметрии за ось абсцисс декартовой прямоугольной системы координат. Тогда точка \(M(x, y)\) переходит в точку \(M^<*>\) с координатами
$$
x^<*>=x,\ y^<*>=-y.\nonumber
$$
Здесь \(c_<1>=c_<2>=0\) и \(\varphi=0\) при нижних знаках в формулах \eqref.

Определение линейных преобразований.

Основным объектом для нас будет более широкий класс преобразований, включающий в себя ортогональные преобразования.

Преобразование \(f\) плоскости \(P\) называется линейным, если на \(P\) существует такая декартова система координат, в которой \(f\) может быть записано формулами
$$
\begin
& x^<*>=a_<1>x+b_<1>y+c_<1>,\\
& y^<*>=a_<2>x+b_<2>y+c_<2>.
\end\label
$$
Взаимно однозначное линейное преобразование называется аффинным преобразованием.

Подчеркнем, что в определении линейного преобразования, вовсе не требуется, чтобы коэффициенты в формулах \eqref не обращались в нуль одновременно. Они могут быть любыми. Докажем следующее утверждение.

Для того чтобы преобразование, задаваемое формулами \eqref, было взаимно однозначным, необходимо и достаточно,
$$
\begin
a_<1>& b_<1>\\
a_<2>& b_<2>
\end \neq 0.\label
$$

Таким образом, аффинное преобразование определяется формулами \eqref при условии \eqref.

Наше утверждение вытекает по существу из утверждения о существовании решения системы линейных уравнений. Нам нужно узнать, при каком условии каждая точка плоскости имеет единственный прообраз. Формулы \eqref связывают координаты \((x^<*>, y^<*>)\) точки \(M^<*>\) и координаты \((x, y)\) ее прообраза. Их можно рассматривать как систему линейных уравнений для нахождения \(x\) и \(y\), и эта система имеет единственное решение при любых свободных членах \(x^<*>-c_<1>\) и \(y^<*>-c_<2>\) (а значит, при любых \(x^<*>\) и \(y^<*>\)) тогда и только тогда, когда выполнено условие \eqref.

Как видно из доказанного утверждения, ортогональные преобразования являются линейными. Проверка условия \eqref показывает, что они аффинные. Рассмотрим другие примеры.

Рассмотрим сжатие к прямой и примем эту прямую за ось абсцисс декартовой прямоугольной системы координат. Легко видеть, что в такой системе координат сжатие с коэффициентом \(\lambda\) записывается формулами
$$
x^<*>=x,\ y^<*>=\lambda y.\nonumber
$$
Сжатие к прямой — аффинное преобразование.

Проектирование на прямую в такой декартовой прямоугольной системе координат, для которой эта прямая — ось абсцисс, записывается формулами
$$
x^<*>=x,\ y^<*>=0.\nonumber
$$
Это — линейное, но не аффинное преобразование.

Для записи уравнений гомотетии не существенно, чтобы система координат была прямоугольной, но уравнения проще, если начало координат поместить в центр гомотетии. По определению гомотетии с коэффициентом \(\lambda\) вектор \(\overrightarrow\) переходит в вектор \(\overrightarrow>=\lambda\overrightarrow\). Если \(O\) — начало координат, координаты точек \(M\) и \(M^<*>\) будут связаны равенствами
$$
x^<*>=\lambda x,\ y^<*>=\lambda y.\nonumber
$$
Гомотетия — аффинное преобразование.

Преобразование, сопоставляющее каждой точке плоскости одну и ту же точку \(C\), записывается формулами \(x^<*>=c_<1>\), \(y^<*>=c_<2>\), где \(c_<1>\) и \(c_<2>\) — координаты точки \(C\). Оно линейное, но не аффинное.

Определение аффинного преобразования содержит упоминание о некоторой определенной системе координат, и заранее не известно, будет ли преобразование записываться формулами вида \eqref в какой-либо другой системе координат. Давайте докажем следующее утверждение.

В любой декартовой системе координат, линейное преобразование задается формулами вида \eqref, то есть:
$$
\begin
& x^<*>=a_<1>x+b_<1>y+c_<1>,\\
& y^<*>=a_<2>x+b_<2>y+c_<2>.
\end\nonumber
$$

Пусть преобразование задано равенствами \eqref в системе координат \(O, \boldsymbol_<1>, \boldsymbol_<2>\). Перейдем к системе координат \(O’, \boldsymbol’_<1>, \boldsymbol’_<2>\). Как мы знаем, старые координаты точки \(M(x, y)\) выражаются через новые координаты \((x’, y’)\) по следующим формулам:
$$
x=\alpha_<1>x’+\beta_<1>y’+\gamma_<1>,\ y=\alpha_<2>x’+\beta_<2>y’+\gamma_<2>.\label
$$
Для образа \(M^<*>\) точки \(M\) нам нужно будет, наоборот, выразить новые координаты \((x’^<*>, y’^<*>)\) через его старые координаты \((x^<*>, y^<*>)\). Они выражаются такими же формулами, разумеется, с другими коэффициентами:
$$
x’^<*>=\lambda_<1>(x^<*>)+\mu_<1>y^<*>+\nu_<1>,\ y’^<*>=\lambda_<2>x^<*>+\mu_<2>y^<*>+\nu_<2>.\label
$$

Нам требуется найти выражение новых координат \((x’^<*>, y’^<*>)\) точки \(M^<*>\) через новые координаты \((x’, y’)\) точки \(M\). С этой целью подставим в равенства \eqref значения \(x^<*>\) и \(y^<*>\) из формул \eqref:
$$
\begin
& x’^<*>=\lambda_<1>(a_<1>x+b_<1>y+c_<1>)+\mu_<1>(a_<2>x+b_<2>y+c_<2>)+\nu_<1>,\\
& y’^<*>=\lambda_<2>(a_<1>x+b_<1>y+c_<1>)+\mu_<2>(a_<2>x+b_<2>y+c_<2>)+\nu_<2>.
\end\nonumber
$$

Для нас важно, что правые части этих равенств — многочлены степени не выше 1 относительно \(x\) и \(y\):
$$
x’^<*>=A_<1>x+B_<1>y+C_<1>,\ y’^<*>=A_<2>x+B_<2>y+C_<2>.\label
$$
Подставив сюда выражения \(x\) и \(y\) по формулам \eqref, мы найдем искомую зависимость:
$$
\begin
& x’^<*>=A_<1>(\alpha_<1>x’+\beta_<1>y’+\gamma_<1>)+B_<1>(\alpha_<2>x’+\beta_<2>y’+\gamma_<2>)+C_<1>,\\
& y’^<*>=A_<2>(\alpha_<1>x’+\beta_<1>y’+\gamma_<1>)+B_<2>(\alpha_<2>x’+\beta_<2>y’+\gamma_<2>)+C_<2>.
\end\nonumber
$$
Мы видим, что правые части этих равенств — многочлены степени не выше 1 относительно \(x’\) и \(y’\). Это нам и требовалось доказать.

Заметим, что аффинные преобразования выделяются из линейных требованием взаимной однозначности, которое не зависит от системы координат. Поэтому без дополнительных проверок мы можем быть уверены, что формулы, задающие аффинное преобразование в новой системе координат, удовлетворяют условию \eqref.

Произведение линейных преобразований.

Доказательство последнего утверждения было основано на том, что результат подстановки многочленов степени не выше 1 в многочлен степени не выше 1 оказывается таким же многочленом. Это же обстоятельство лежит в основе следующего утверждения.

Произведение линейных преобразований является линейным преобразованием. Произведение аффинных преобразований — аффинное преобразование.

Пусть заданы линейные преобразования \(f\) и \(g\) и выбрана система координат. Тогда координаты точки \(f(M)\) выражаются через координаты точки \(M\) формулами
$$
x^<*>=a_<1>x+b_<1>y+c_<1>,\ y^<*>=a_<2>x+b_<2>y+c_<2>.\label
$$
а координаты точки \(g(f(M))\) через координаты точки \(f(M)\) формулами
$$
x^<**>=d_<1>x^<*>+e_<1>y^<*>+f_<1>,\ y^<**>=d_<2>x^<*>+e_<2>y^<*>+f_<2>.\label
$$
Подстановка равенств \eqref в \eqref выражает координаты g(f(M)) через координаты \(M\). В результате подстановки мы получаем многочлены степени не выше 1, что и доказывает первую часть предложения.

Для доказательства второй части достаточно вспомнить, что по согласно ранее доказанного утверждения произведение двух взаимно однозначных преобразований взаимно однозначно.

Преобразование, обратное аффинному преобразованию, также является аффинным.

Если преобразование \(f\) записано уравнениями \eqref, то координатная запись его обратного преобразования получается решением уравнений \eqref относительно \(x\) и \(y\). Для того чтобы решить эти уравнения, умножим первое из них на \(b_<2>\), второе — на \(b_<1>\) и вычтем одно уравнение из другого. Мы получим \((a_<1>b_<2>-a_<2>b_<1>)x=b_<2>(x^<*>-c_<1>)-b_<1>(y^<*>-c_<2>)\). Из условия \eqref следует, что \(x\) — линейный многочлен от \(x^<*>\) и \(y^<*>\). Выражение для \(y\) получается аналогично.

Образ вектора при линейном преобразовании.

Рассмотрим вектор \(\overrightarrowM_<2>>\). Если координаты точек \(M_<1>\) и \(M_<2>\) в системе координат \(O, \boldsymbol_<1>, \boldsymbol_<2>\) обозначить соответственно \(x_<1>, y_<1>\) и \(x_<2>, y_<2>\), то компоненты вектора будут равны \(x_<2>-x_<1>\) и \(y_<2>-y_<1>\). Пусть формулы \eqref задают преобразование \(f\) в выбранной системе координат. Тогда образы \(M_<2>^<*>\) и \(M_<1>^<*>\) точек \(M_<2>\) и \(M_<1>\) имеют абсциссы
$$
x_<2>^<*>=a_<1>x_<2>+b_<1>y_<2>+c_<1>,\ x_<1>^<*>=a_<1>x_<1>+b_<1>y_<1>+c_<1>.\nonumber
$$
Следовательно, первая компонента вектора \(\overrightarrow^<*>M_<2>^<*>>\) равна
$$
x_<2>^<*>-x_<1>^<*>=a_<2>(x_<2>-x_<1>)+b_<1>(y_<2>-y_<1>).\nonumber
$$
Аналогично находим вторую компоненту этого вектора
$$
y_<2>^<*>-y_<1>^<*>=a_<2>(x_<2>-x_<1>)+b_<2>(y_<2>-y_<1>).\nonumber
$$

Обратим внимание на то, что компоненты \(\overrightarrow^<*>M_<2>^<*>>\) выражаются только через компоненты \(\overrightarrowM_<2>>\), а не через координаты точек \(M_<1>\) и \(M_<2>\) по отдельности. Два равных вектора имеют одинаковые компоненты и, следовательно, при линейном преобразовании перейдут в векторы, компоненты которых также одинаковы. Итак, мы получаем ещё одно утверждение.

При линейном преобразовании равные векторы переходят в равные векторы. Компоненты \(\alpha_<1>^<*>\), \(\alpha_<2>^<*>\) образа вектора выражаются через его компоненты \(\alpha_<1>\), \(\alpha_<2>\) формулами
$$
\begin
& \alpha_<1>^<*>=a_<1>\alpha_<1>+b_<1>\alpha_<2>,\\
& \alpha_<2>^<*>=a_<2>\alpha_<1>+b_<2>\alpha_<2>.
\end\label
$$

Если быть точным, говорить об образе вектора при преобразовании \(f\) неправильно: преобразование отображает точки, а не векторы. Точнее было бы сказать, что \(f\) порождает преобразование \(\tilde\) множества векторов. Но ниже мы, тем не менее, будем придерживаться не совсем точной, но более удобной и общепринятой терминологии — говорить, что преобразование \(f\) переводит вектор \(\boldsymbol\) в вектор \(\boldsymbol^<*>\) и обозначать последний через \(f(\boldsymbol)\).

Из равенств \eqref следует, что при линейном преобразовании \(f\) линейно зависимые векторы переходят в линейно зависимые. Действительно, как легко видеть, \(f(\boldsymbol<0>)=\boldsymbol<0>\). Тогда любое соотношение вида \(\lambda \boldsymbol+\mu \boldsymbol=\boldsymbol<0>\) влечет за собой \(\lambda f(\boldsymbol)+\mu f(\boldsymbol)=\boldsymbol<0>\).

Следующее утверждение устанавливает геометрический смысл коэффициентов в формулах, задающих линейное преобразование.

Пусть преобразование \(f\) записано в системе координат \(O, \boldsymbol_<1>, \boldsymbol_<2>\) формулами \eqref. Тогда \(c_<1>\) и \(c_<2>\) — координаты точки \(f(O)\), a \(a_ <1>a_<2>\) и \(b_<1>, b_<2>\) — компоненты векторов \(f(\boldsymbol_<1>)\) и \(f(\boldsymbol_<2>)\) в системе координат \(O, \boldsymbol_<1>, \boldsymbol_<2>\).

Для доказательства подставим в формулы \eqref значения \(x=0\) и \(y=0\) координат точки \(O\) и увидим, что координаты \(f(O)\) равны \(c_<1>\) и \(c_<2>\).

Подставим в формулы \eqref координаты вектора \(\boldsymbol_<1>\) \(\alpha_<1>=1\), \(\alpha_<2>=0\) и найдем \(a_<1>^<*>=a_<1>\), \(a_<2>^<*>=a_<2>\). Следовательно, \(f(\boldsymbol_<1>)\) имеет компоненты \(a_<1>\) и \(a_<2>\). Так же доказывается, что компоненты \(f(\boldsymbol_<2>)\) равны \(b_<1>\) и \(b_<2>\).

Каковы бы ни были три точки \(L\), \(M\), \(N\), не лежащие на одной прямой, и три точки \(L^<*>\), \(M^<*>\) и \(N^<*>\), существует единственное линейное преобразование \(f\) такое, что \(L^<*>=f(L)\), \(M^<*>=f(M)\) и \(N^<*>=f(N)\). Это преобразование аффинное тогда и только тогда, когда точки \(L^<*>\), \(M^<*>\) и \(N^<*>\) также не лежат на одной прямой.

Векторы \(\overrightarrow\) и \(\overrightarrow\) не коллинеарны. Следовательно, \(L\), \(\overrightarrow\), \(\overrightarrow\) — декартова система координат. Пусть \(c_<1>, c_<2>\) — координаты \(L^<*>\), а \(a_<1>, a_<2>\) и \(b_<1>, b_<2>\) — компоненты векторов \(\overrightarrowM^<*>>\) и \(\overrightarrowN^<*>>\) в этой системе координат. Формулы
$$
x^<*>=a_<1>x+b_<1>y+c_<1>,\ y^<*>=a_<2>x+b_<2>y+c_<2>\nonumber
$$
определяют линейное преобразование \(f\), которое, как легко видеть, обладает требуемым свойством. При этом согласно предложению 7, коэффициенты в формулах однозначно определены.

Условие \eqref, равносильное аффинности преобразования, необходимо и достаточно для того, чтобы векторы \(\overrightarrowM^<*>>\) и \(\overrightarrowN^<*>>\) были не коллинеарны, то есть \(L^<*>\), \(M^<*>\) и \(N^<*>\) не лежали на одной прямой. Предложение доказано.

Заметим, что в том случае, когда преобразование \(f\) аффинное, точка \(f(O)\) и векторы \(f(\boldsymbol_<1>)\) и \(f(\boldsymbol_<2>)\) могут быть использованы как система координат. Для этой системы координат имеет место ещё одно утверждение.

При аффинном преобразовании \(f\) образ \(M^<*>\) точки \(M\) в системе координат \(f(O)\), \(f(\boldsymbol_<1>)\), \(f(\boldsymbol_<2>)\) имеет те же координаты, что и точка \(M\) в системе координат \(O, \boldsymbol_<1>, \boldsymbol_<2>\).

Равенство \(\overrightarrow=x \boldsymbol_<1>+y \boldsymbol_<2>\) означает, что \(x\), \(y\) — координаты \(M\) в системе координат \(O, \boldsymbol_<1>, \boldsymbol_<2>\). Подействовав преобразованием \(f\) на обе части этого равенства, мы получаем \(\overrightarrow=x f(\boldsymbol_<1>)+y f(\boldsymbol_<2>)\), которое означает, что \(x\) и \(y\) — координаты \(M^<*>\) в системе координат \(f(O)\), \(f(\boldsymbol_<1>)\), \(f(\boldsymbol_<2>)\).

Источник