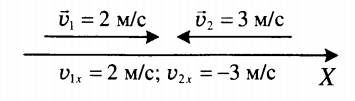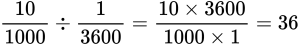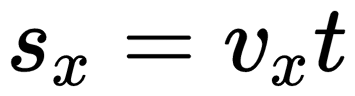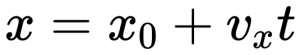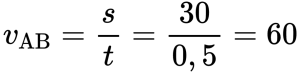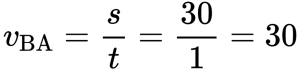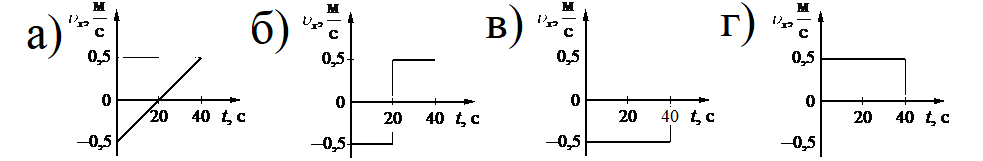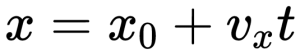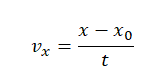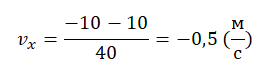Докажите что при равномерном прямолинейном движении точки в плоскости x0y под углом

§ 4. Равномерное прямолинейное движение. Скорость. Уравнение движения (окончание)

Выберем оси координат так, чтобы точка двигалась по какой-либо оси, например по оси ОХ. Тогда векторы ₀ и будут составлять с осями OY и OZ прямой угол. Поэтому их проекции на эти оси равны нулю. А значит, равны нулю в любой момент времени и проекции радиус-вектора ₀ на оси OY и OZ. Так как проекции радиус- вектора на координатные оси равны координатам его конца, то r_х = х и r_0х = х₀. Поэтому в проекциях на ось ОХ уравнение (1.4) можно записать в виде

Запомни
Уравнение (1.5) есть уравнение равномерного прямолинейного движения точки, записанное в координатной форме.

Оно позволяет найти координату х точки при этом движении в любой момент времени, если известны проекция её скорости на ось ОХ и её начальная координата х₀.

Если ₀ и не совпадают по направлению, а ось ОХ направлена вдоль скорости, то уравнение движения запишем в виде

x = x₀ + _xt
y = y₀
z = z₀,

где х₀, у₀, z₀ — проекции радиус-вектора ₀ на оси координат (рис. 1.10, а).

Какое из наблюдаемых вами движений можно приблизительно считать равномерным?

Отметим, что, строго говоря, равномерного прямолинейного движения не существует. Автомобиль на шоссе никогда не едет абсолютно прямо, небольшие отклонения в ту или иную сторону от прямой всегда имеются. И значение скорости слегка изменяется. Но приближённо на протяжении не слишком большого промежутка времени движение автомобиля можно считать равномерным и прямолинейным с достаточной для практических целей точностью. Таково одно из упрощений действительности, позволяющее без больших усилий описывать многие движения.

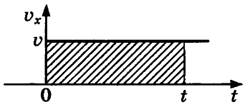
Графическое представление равномерного прямолинейного движения. Полученные результаты можно изобразить наглядно с помощью графиков. Особенно прост график зависимости проекции скорости от времени (рис. 1.11). Это прямая, параллельная оси времени. Площадь прямоугольника ОАВС, заштрихованная на рисунке, равна изменению координаты точки за время t. Ведь сторона ОА есть υ_x, а сторона ОС — время движения t, поэтому Δ_x = υ_xt.

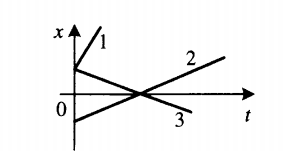
На рисунке 1.12 приведены примеры графиков зависимости координаты от времени для трёх различных случаев равномерного прямолинейного движения. Прямая 1 соответствует случаю х₀ = 0, υ_x1 > 0; прямая 2 — случаю х₀ 0, а прямая 3 — случаю х₀ > 0, υ_x3 Образцы заданий ЕГЭ

A1. Зависимость координаты точки от времени при равномерном прямолинейном движении выражается

1) линейной функцией 3) тригонометрической функцией
2) квадратичной функцией 4) показательной функцией

A3. В таблице приведены координаты корабля, плывущего по прямому каналу.

Согласно данным таблицы, движение корабля является

Источник

Равномерное прямолинейное движение

теория по физике 🧲 кинематика

Равномерное прямолинейное движение — это такое движение, при котором тело совершает за любые равные промежутки времени равные перемещения.

Скорость при прямолинейном равномерном движении

Если тело движется равномерно и прямолинейно, его скорость остается постоянной как по модулю, так и по направлению. Ускорение при этом равно нулю.

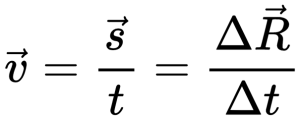
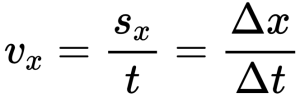
Векторный способ записи скорости при равномерном прямолинейном движении:s — вектор перемещения, ΔR— изменение радиус-вектора, t — время, а ∆t — его изменение. Проекция скорости на ось ОХ: s_x — проекция перемещения на ось ОХ, ∆x — изменение координаты точки (ее абсциссы). Знак модуля скорости зависит от направления вектора скорости и оси координат:

Основная единица измерения скорости — 1 метр в секунду. Сокращенно — 1 м/с.

Спидометр — прибор для измерения модули скорости тела.

График зависимости скорости от времени представляет собой прямую линию, перпендикулярную оси скорости и параллельную оси времени. Выглядит он так:

Чтобы сравнить модули скоростей на графике, нужно оценить их удаленность от оси времени. Чем дальше график от оси, тем больше модуль.

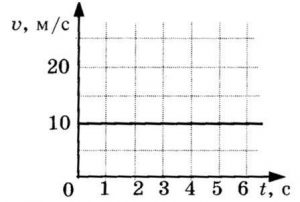
Пример №1. Найти модуль скорости и направление движения тела относительно оси ОХ. Выразить скорость в км/ч.

График скорости пересекает ось в точке со значением 10. Единица измерения — м/с. Поэтому модуль скорости равен 10 м/с. График лежит выше оси времени. Это значит, что тело движется по направлению оси ОХ. Чтобы выразить скорость в км/ч, нужно перевести 10 м в километры и 1 с в часы:

Теперь нужно разделить километры на часы:

Перемещение и координаты тела при равномерном прямолинейном движении

Геометрический смысл перемещения заключается в том, что его модуль равен площади фигуры, ограниченной графиком скорости, осями скорости и времени, а также линией, проведенной перпендикулярно оси времени.

При прямолинейном равномерном движении эта фигура представляет собой прямоугольник. Поэтому модуль перемещения вычисляется по следующей формуле:

Вектор перемещения равен произведению вектора скорости на время движения: Внимание!

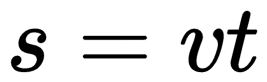
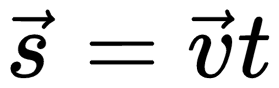
При равномерном прямолинейном движении путь и перемещение совпадают. Поэтому путь, пройденный телом, можно найти по этим же формулам.

Формула проекции перемещения:

График проекции перемещения

График проекции перемещения показывает зависимость этой проекции от времени. При прямолинейном равномерном движении он представляет собой луч, исходящий из начала координат. Выглядит он так:

Чтобы по графику проекции перемещения сравнить модули скоростей, нужно сравнить углы их наклона к оси s_x.Чем меньше угол, тем больше модуль. Согласно рисунку выше, модули скорости тел, которым соответствуют графики 1 и 3, равны. Они превосходят модуль скорости тела 2, так как их угол наклона к оси s_x меньше.

График координаты

График координаты представляет собой график зависимости координаты от времени. Выглядит он так:

Так как график координаты представляет собой график линейной функции, уравнение координаты принимает вид :

Чтобы сравнить модули скоростей тел по графику координат, нужно сравнить углы наклона графика к оси координат. Чем меньше угол, тем больше модуль скорости. На картинке выше наибольший модуль скорости соответствует графику 1. У графиков 2 и 3 модули равны.

Чтобы по графику координат найти время встречи двух тел, нужно из точки пересечения их графиков провести перпендикуляр к оси времени.

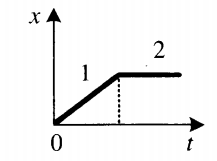
Пример №2. График зависимости координаты тела от времени имеет вид:

Изучите график и на его основании выберите два верных утверждения:

На участке 1 координата растет, и ее график представляет собой прямую. Это значит, что на этом участке тело движется равномерно (с постоянной скоростью). На участке 2 координата с течением времени не меняется, что говорит о том, что тело покоится. Исходя из этого, верными утверждениями являются номера 1 и 3.

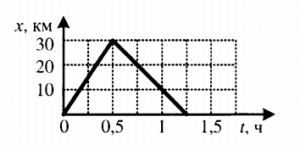
Пример №3. На рисунке изображен график движения автомобиля из пункта А (х=0 км) в пункт В (х=30 км). Чему равна минимальная скорость автомобиля на всем пути движения туда и обратно?

Согласно графику, с начала движения до прибытия автомобиля в пункт 2 прошло 0,5 часа. А с начала движения до возвращения в пункт А прошло 1,5 часа. Поэтому время, в течение которого тело возвращалось из пункта В в пункт А, равно:

Туда и обратно автомобиль проходил равные пути, каждый из которых равен 30 км. Поэтому скорость во время движения от А к В равна:

Скорость во время движения от В к А равна:

Минимальная скорость автомобиля на всем пути движения составляет 30 км/ч.

На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Скорость второго тела v₂ больше скорости первого тела v₁ в n раз, где n равно…

Алгоритм решения

Решение

Рассмотрим графики во временном интервале от 0 до 4 с. Ему соответствуют следующие данные:

Скорость определяется формулой:

Так как начальный момент времени и скорость для обоих тел нулевые, формула примет вид:

Скорость первого тела:

Скорость второго тела:

Отношение скорости второго тела к скорости первого тела:

pазбирался: Алиса Никитина | обсудить разбор | оценить

На рисунке приведён график зависимости координаты тела от времени при прямолинейном движении тела по оси Ox.

Алгоритм решения

Уравнение координаты при равномерном прямолинейном движении имеет вид:

Отсюда проекция скорости равна:

Начальная координата x_o = 10 м, конечная x = –10 м. Общее время, в течение которого двигалось тело, равно 40 с.

Вычисляем проекцию скорости:

Этому значению соответствует график «в».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Весь график можно поделить на 3 участка:

По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t₁ = 20 c до t₂ = 50 с. Этому времени соответствуют два участка:

Записываем формулу искомой величины:

s₁ — путь тела, пройденный на первом участке, s₂ — путь тела, пройденный на втором участке.

s₁и s₂ можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s₁и s₂, а затем сложим их:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник

ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ

МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

РОССИЙСКОЙ ФЕДЕРАЦИИ

РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

СБОРНИК ЗАДАЧ ПО ФИЗИКЕ

( для студентов педагогической специальности физических факультетов университетов)

Печатается по решению учебно-методической комиссии физического

Протокол № от 2003 г.

Сборник задач по физике (для студентов педагогической специальности физических

факультетов университетов). Л.М. Монастырский, В.И. Махно. – 2-е изд.-

Ростов н/Д, 2003 г., стр. –20.

Сборник задач представляет собой первую часть задачника по курсу общей физики для

студентов педагогической специальности физических факультетов университетов. Задачи подобраны с целью плавного перехода от курса физики, изучаемого в средней школе, к курсу общей физики.

Сборник задач предназначен для аудиторных и домашних занятий студентов педагогической специальности физических факультетов университетов. Сборник составлен на основе задачников по физике, используемых в средних общеобразовательных и высших учебных заведениях. Задачи снабжены ответами.

В первую часть задачника включены задачи по кинематике. Расположение задач соответствует структуре учебной программы раздела механики курса общей физики для студентов-педагогов физического факультета РГУ.

При работе над задачником была использована следующая литература:

ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ

1.1. Два одинаковых вектора длиной 4 см перпендикулярны друг другу. Определите длину вектора суммы и его направление по отношению к слагаемым векторам.

1.2. Даны два вектора, расположенные на одной прямой и одинаково направленные. Докажите, что модуль вектора суммы равен сумме модулей векторов слагаемых.

1.3. Два вектора расположены на одной прямой и направлены в противоположные стороны. Докажите, что модуль вектора суммы будет равен разности модулей слагаемых векторов.

1.4. Может ли приращение модуля вектора оказаться равным модулю приращения вектора ?

1.5. Вектор изменил направление на обратное. Найти .

1.6. В координатах х,у положение точки задано М(5,5). Определить модуль ее радиус-вектора и угол, который он составляет с осью Ох.

1.7. Даны точки М₁(2,10) и М₂(5,6). Определить модуль вектора М₁М₂.

1.8. Построить график зависимости скалярного произведения векторов и от угла между ними.

1.9. Выразить радиус-вектор середины отрезка АВ через радиус-векторы и точек А и В.

1.11. Вектор силы, величина которой 10 Н, направлен под углом 30 0 к оси х. Представить его в виде суммы составляющих по осям ох и оу.

1.12. Вектор направлен под углом 30 0 к оси ох, а вектор направлен под углом 90 0 к вектору . Найти : а) проекции векторов на оси ох и оу, б) модуль разности векторов и в) модуль суммы векторов.

КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ

ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ

2.1. Точка движется по прямой. При этом за любой интервал времени длительностью 1 с она проходит путь длиной 1 м. Можно ли утверждать, что точка движется равномерно?

2.3. Точка движется с постоянной скоростью под углом к оси ох (рис.1). В начальный момент времени t=0 точка имела координаты (x₀, y₀). Написать уравнение движения точки и уравнение траектории.

y₀

0

2.5. Поезд, вышедший в 12 ч дня из пункта А, движется со скоростью 60 км/ч. Поезд, вышедший в 2 ч дня из пункта В, движется со скоростью 40 км/ч навстречу первому поезду. Определить место встречи, если расстояние АВ равно 420 км.

2.6. По прямому шоссе в одном направлении движутся два мотоциклиста. Скорость первого мотоциклиста 10 м/с. Второй догоняет его со скоростью 20 м/с. Расстояние между мотоциклистами в начальный момент времени равно 200 м. Написать уравнение движений мотоциклистов в системе отсчета, связанной с землей, приняв за начало координат место нахождения второго мотоциклиста в начальный момент времени и выбрав за положительное направление оси ох направление движения мотоциклистов. Построить на одном чертеже графики движения обоих мотоциклистов время и место встречи мотоциклистов.

2.7. Автобус и мотоциклист движутся навстречу друг другу со скоростями, соответственно равными 10 и 20 м/с. Расстояние между ними в момент начала наблюдения равно 600 м. Считая, что ось ох направлена в сторону движения автобуса и при t=0 положение автобуса совпадает с началом отсчета написать для автобуса и мотоциклиста уравнение х=х(t). Найти:

а) время и место встречи автобуса и мотоциклиста;

б) расстояние между ними через 10 с;

в) положение мотоциклиста в тот момент времени, когда автобус проходит точку

с координатой 250 м;

г) в какие моменты времени расстояние между автобусом и мотоциклистом было

2.8. Движение материальной точки задано уравнениями х= 2+t и у= 1 + 2t. Написать уравнение траектории и построить ее график на плоскости хОу.

2.9. Найти время и место встречи тел, графики движения которых приведены на рис.2.

x, м

10

120 0

60 0

0 t, с

2.10. Радиус-вектор частиц задан уравнением:

Определить модуль и направление скорости, перемещение и его модуль за 10с, путь

за 10 с, построить траекторию частицы на плоскости хоу.

2.11. Скорость частицы задана уравнением:

Определить модуль скорости, перемещение и его модуль за 5 с, путь за 5 с.

2.12. Два автопоезда движутся навстречу друг другу по прямому шоссе со скоростями

72 км/ч и 54 км/ч. В некоторый момент времени они оказываются на расстоянии 40 и 30 км соответственно от середины узкого участка шоссе, на котором возможно только одностороннее движение. Длина этого участка 1,5 км. Помешают ли автопоезда друг другу при проезде этого участка?

2.17. На листе бумаги начерчен прямой угол. Линейка, оставаясь все время перпендикулярной к биссектрисе этого угла, движется со скоростью 10 м/с. С какой скоростью движутся по сторонам угла их пересечения с линейкой?

2.19. По шоссе со скоростью 16 м/с движется автобус. Человек находится на расстоянии 60 м от шоссе и 400 м от автобуса. В каком направлении должен бежать человек, чтобы выйти к какой-либо точке шоссе одновременно с автобусом или раньше его? Человек может бежать со скоростью 4 м/с. При какой наименьшей скорости человек может встретить автобус? В каком направлении должен при этом бежать человек?

2.20. Человек, идущий с постоянной по величине и направлению скоростью V, проходит под фонарем, висящим на высоте H. Найти скорость перемещения края тени от головы человека, если его высоты h.

НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ

3.1. По графику зависимости координаты тела от времени ( рис.3) построить графики зависимостей ускорения, скорости и пути, пройденного телом, от времени. Начальная скорость равна нулю.

3.2. Дан график зависимости скорости тела от времени (рис. 4). Построить графики зависимости пути и координаты от времени. Определить среднюю скорость за первые 2 и 5 с. Начальная координата равна нулю.

V(м/с)

3

0 2 4 6 t, c

-3

3.6. Свободно падающее тело за последнюю секунду падения прошло 1/3 своего пути. Найти время падения и высоту, с которой упало тело.

3.7. Свободно падающее тело прошло последние 30 м за время 0,5 с. Найти высоту падения.

3.8. Частица движется вдоль оси х так, что зависимость ее координаты от времени дается графиком, изображенным на рис. 5. Определить характер движения частицы и привести график зависимости пройденного ею пути от времени. Где оказывается частица в момент времени t₅?

3.10. Радиус-вектор частицы определяется выражением : . Вычислить: а) путь, пройденный частицей за первые 10 с движения, б) модуль перемещения за то же время.

3.11.Радиус-вектор частицы изменяется со временем по закону : .

Найти : а) скорость и ускорение частицы, б) модуль скорости в момент времени t=1с.

3.12.Частица движется со скоростью . Найти : а) перемещение частицы за первые 2 с ее движения; б) модуль скорости в момент времени t=2 с.

3.13.Частица движется со скоростью . Найти :

а) модуль скорости частицы в момент времени t=1 с;

б) ускорение частицы и его модуль;

в) путь, пройденный частицей с момента t₁=2 с до момента t₂=3 с.

3.14.Радиус-вектор частицы меняется со временем по закону , где -постоянный вектора, — положительная постоянная. Найти:

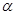
а) скорость частицы и ее ускорение в зависимости от времени;

3.15.Радиус-вектор точки А относительно начала координат меняется со временем по закону где и — постоянные. Найти:

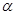
а) уравнение траектории точки у =у(x); изобразить ее график;

б) зависимость от времени скорости точки, ускорения и модулей этих величин;

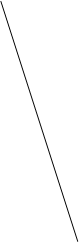
в) зависимость от времени угла между векторами ускорения и скорости.

3.16.Точка движется в плоскости ху по закону , где и — положительные постоянные. Найти:

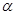
а) уравнение траектории точки у(x); изобразить ее график;

б) скорость и ускорение точки в зависимости от времени;

в) момент времени t₀, когда угол между скоростью и ускорением равен

3.17.Компоненты скорости частицы изменяются со временем по законам , где и -константы. Найти модули скорости и ускорения, а также угол между векторами скорости и ускорения.

3.18.Зависимость координат движения частицы от времени имеет вид .

а) определить радиус-вектор частицы , скорость , ускорение , а также их модули.

б) вычислить скалярное произведение векторов и .

в) вычислить скалярное произведение векторов .

г) найти уравнение траектории, изобразить ее график и указать направление движения частицы по траектории.

3.19.Точка движется в плоскости ху по закону , где А и -положительные постоянные. Найти: а) путь, пройденный точкой за время ; б) угол между скоростью и ускорением точки.

3.20.По графику зависимости ускорения от времени (рис.6) построить графики зависимости , считая, что .

а(м/с 2 )

3.21.Лодку с крутого берега тянут за веревку, выбирая ее с постоянной по модулю скоростью V. Найдите зависимость модуля скорости лодки от угла между веревкой и горизонтальным направлением.

Дата добавления: 2018-11-24 ; просмотров: 356 ; Мы поможем в написании вашей работы!

Источник