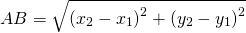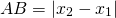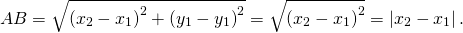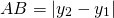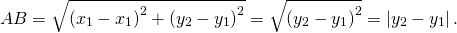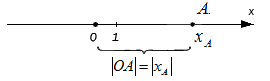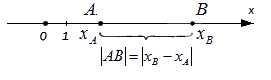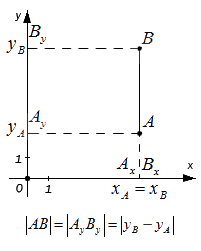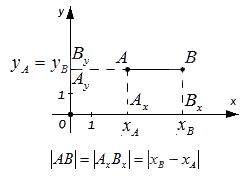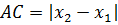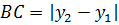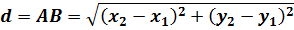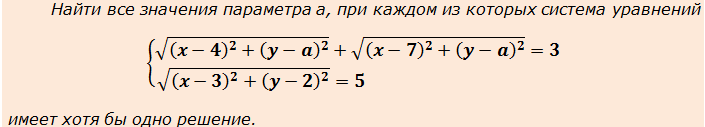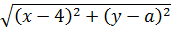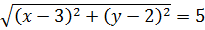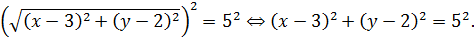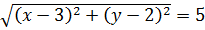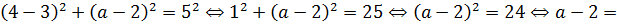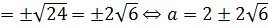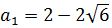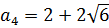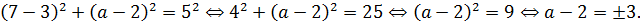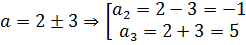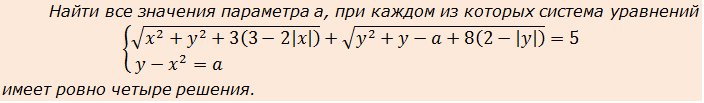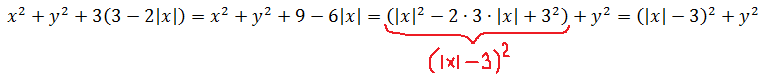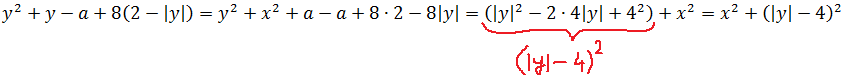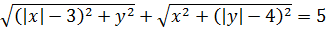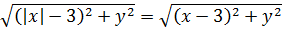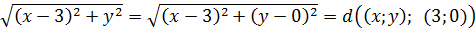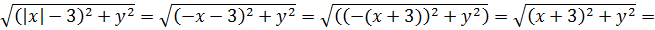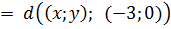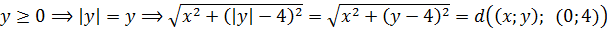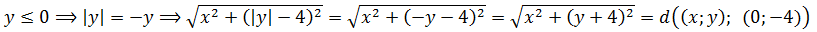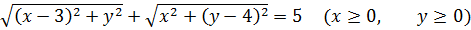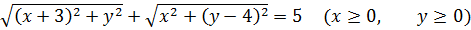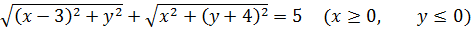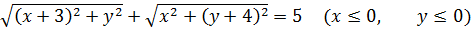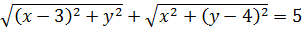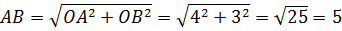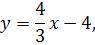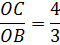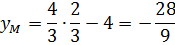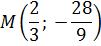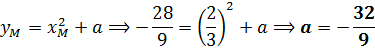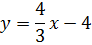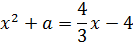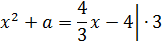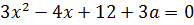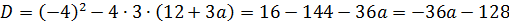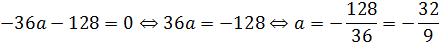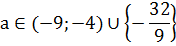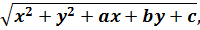Формула расстояния между точками

Формула для нахождения расстояния между двумя точками A(x1;x2) B(x2;y2) на плоскости:

Сначала рассмотрим частные случаи.

1) Если y1=y2,

К этой же формуле придём, если подставим координаты точек A и B в общую формулу:

2) Аналогично, если x1=x2:

Эту же формулу получим, подставив координаты A и B в общую формулу:

3) Если x1=x2 и y1=y2, AB=0. Формула для этого случая также верна.

Проведём через точки A и B прямые, перпендикулярные координатным осям. Обозначим точку пересечения этих прямых через C.

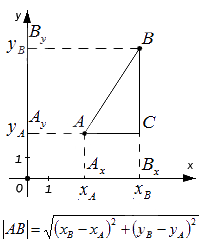
Из прямоугольного треугольника ABC по теореме Пифагора

Источник

Урок 3

расстояние между двумя точками.

деление отрезка в данном отношении.

Расстояние между двумя точками.

так как Полученный треугольник Прямоугольный, то По теореме Пифагора

Пример 1. найти расстояние между точками а(-2;3) и в(5;4).

решение. исПользуя данную формулу, Получим:&amP;NbSP;

уПражнение. даны точки а(0;0), в(3;-4), с(-3;4). найдите расстояние между точками: а) аи в; б) в и с; в) а и с. (ответ: а) 5, б) 10, в) 5)

доказательство. Площадь треугольника авс, изображенного на рисунке, можно найти так:

выражая Площадь каждой траПеции через координаты точек а, в и с, находим:

S adec =1/2 (ad+ce)*de = 1/2( x 3 – x 1 )( y 3 + y 1 )

S bceF =1/2 (ec+bF)*eF = 1/2 ( x 2 – x 3 )( y 2 + y 3 )

S abFd =1/2 (ad+bF)*dF = 1/2 ( x 2 – x 1 )( y 2 + y 1 )

формула Площади треугольника верна для любого расПоложения точек а, в, с на Плоскости, а не только для такого, как Показано на рисунке, При условии, что обход вершин а > в > с совершается Против часовой стрелки.

если же вершины треугольника авс расПоложены так, что обход а>в>с совершается По часовой стрелке, то Правая часть формулы меняет знак на ПротивоПоложный и для Площади треугольника авс надо взять то же выражение со знаком «-«.

Пример 2. даны точки а(1;1), в(6;4), с(8;2). найти Площадь треугольника авс.

решение. Подставляя координаты точек в формулу для Площади треугольника, Получим:

S abc =1/2 |(6 – 1)(2 –1) – (8 – 1)(4 – 1)| = 1/2 l-16l =8

уПражнение. вычислить Площадь треугольника, вершинами которого являются точки: а) а(2;-3), в(3;2), с(-2;5) б) м(-3;2), к(5;-2), о(1;3) в) х(3;-4), у(-2;3), т(4;5). (ответ: а) 14, б) 12, в) 25).

Деление отрезка в данном отношении.

задача о делении отрезка в данном отношении состоит в том, чтобы По данному отношению Л и данным координатам точек м 1, м 2 найти координаты точки м.

эту задачу Позволяет решить следующая теорема.

Пример 3. даны точки а(-2;3) и в(4;6). отрезок, ограниченный этими точками, разделен в отношении Л =2. найдите координаты точки м(х;у).

решение. Подставим координаты точек и Л =2 в формулы, Получим: х= (-2+2*4) / (1+2)=2; у= (3+2*6) / (1+2)=5. следовательно, координаты точки деления м(2;5).

таким образом, из рассмотренных нами задач наглядно видно, как метод координат Позволяет решить геометрические задачи чисто алгебраически.

на оси ох найдите точку, расстояние которой от точки а(3;4) равно 5. (ответ: (6;0) и (0;0))

точка м является серединой отрезка оа, соединяющего начало координат о с точкой а(-5;2). найдите координаты точки м. (ответ: (-2,5;1))

точка м(2;3) делит отрезок ав в отношении 1:2. найдите координаты точки в, если известно, что точка а имеет координаты (1;2). (ответ: в(4;5))

найдите координаты центра тяжести однородной Пластинки, имеющей форму треугольника с вершинами а(-2;1), в(2;-1), с(4;3).(ответ: х=4 / 3, у=1, указание: центр тяжести треугольника находится в точке Пересечения его медиан, которая делит каждую из медиан в отношении 2:1, считая от вершины)

три вершины Параллелограмма- точки а(3;7), в(2;-3) и с(-1;4). найдите длину высоты, оПущенной из вершины в на сторону ас. (ответ: 7 или 4)

отрезок, ограниченный точками а(1;-3) и в(4;3), разделен на три равные части. оПределите координаты точек деления. (ответ: (2;-1) и (3;1))

оПределите координаты концов отрезка а и в, который точками к(2;2) и м(1;5) разделен на три равные части. (ответ: а(3;-1) и в(0;8))

найдите Площадь Пятиугольника с вершинами о(0;0), а(3;-2), в(5;-1), с(8;4) и е(4;5). (ответ: 29,5)

Источник

Расстояние от точки до точки: формулы, примеры, решения

В данной статье рассмотрим способы определить расстояние от точки до точки теоретически и на примере конкретных задач. И для начала введем некоторые определения.

Расстояние между точками – это длина отрезка, их соединяющего, в имеющемся масштабе. Задать масштаб необходимо, чтобы иметь для измерения единицу длины. Потому в основном задача нахождения расстояния между точками решается при использовании их координат на координатной прямой, в координатной плоскости или трехмерном пространстве.

Расстояние между точками на координатной прямой

В целом можно говорить о том, что оценка длины некого отрезка происходит в сравнении с отрезком, принятым за единицу длины в заданном масштабе.

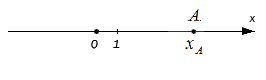
Если точке А соответствует целое действительное число, отложив последовательно от точки О до точки по прямой О А отрезки – единицы длины, мы можем определить длину отрезка O A по итоговому количеству отложенных единичных отрезков.

Резюмируя: расстояние от начала отсчета до точки, которой соответствует действительное число на координатной прямой, равно:

При этом очевидно, что сама длина отрезка не может быть отрицательной, поэтому, используя знак модуля, запишем расстояние от точки O до точки A с координатой x A : O A = x A

Расстояние между точками на плоскости

— если точки А и В совпадают, то расстояние между ними равно нулю;

— если точки A и B не лежат на прямой, перпендикулярной одной из координатных осей, найдем расстояние между ними, выведя формулу расчета:

Сформируем вывод из полученного результата: расстояние от точки А до точки В на плоскости определяется расчётом по формуле с использованием координат этих точек

Для ситуации, когда точки A и B лежат на прямой, перпендикулярной оси абсцисс:

Для случая, когда точки A и B лежат на прямой, перпендикулярной оси ординат:

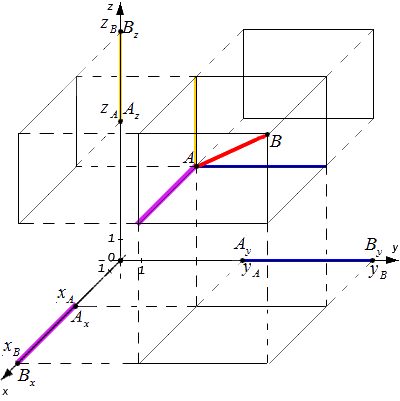
Расстояние между точками в пространстве

Из курса геометрии известно, что квадрат диагонали параллелепипеда равен сумме квадратов его измерений. Исходя из этого утверждения получим равенство: A B 2 = A x B x 2 + A y B y 2 + A z B z 2

Используя полученные ранее выводы, запишем следующее:

Итоговая формула для определения расстояния между точками в пространстве будет выглядеть следующим образом:

Полученная формула действительна также для случаев, когда:

— лежат на одной координатной оси или прямой, параллельной одной из координатных осей.

Примеры решения задач на нахождение расстояния между точками

Решение

Решение

А также используем имеющееся условие, что А В = 5 и тогда будет верным равенство:

λ 2 + 16 = 5 λ 2 + 16 = 25 λ = ± 3

Решение

Источник

Графические методы решения задач с параметрами. Расстояние между точками.

Графические способы решения задач с параметрами. Формула расстояния между двумя точками на плоскости.

В данном материале будет рассмотрен один из очень красивых геометрических методов решения задач с параметрами — метод расстояний. А именно — применение формулы расстояния между двумя точками прямоугольной декартовой системы координат OXY.

Выводится она довольно просто.

Как видно из рисунка, отрезок АВ является гипотенузой прямоугольного треугольника АВС с катетами АС и ВС. Их длины равны разности абсцисс и ординат концов А и В отрезка АВ:

Модули ставятся для того, чтобы было неважно, как именно ориентирован наш отрезок и какая из координат больше — первая или вторая: модуль просто отсекает возможный минус, если, вдруг, скажем, х₂ окажется меньше, чем х₁. Ведь длина отрезка, очевидно, величина неотрицательная.

Теперь, призвав на помощь тяжёлую артиллерию великую и могучую теорему Пифагора, получим наше искомое расстояние:

.

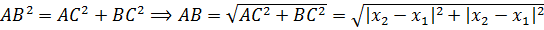
Поскольку как квадрат, так и модуль обладают одним весьма удобным и замечательным свойством — чётностью, то модули под корнем можно совершенно спокойно и без последствий заменить на обычные скобки. 🙂

Вот такая полезная формула. Что ж, на этом краткая теоретическая часть закончена. Пора теперь посмотреть, как именно эта формула работает на примере некоторых задач с параметрами из профильного ЕГЭ по математике.

Пример 1

Иными словами, от нас требуется найти такие а, при которых система имеет решение в принципе. Хотя бы одно. Ни сами решения, ни их количество находить при этом не нужно.

Проанализируем наши уравнения.

Нет, надо идти каким-то обходным путём. Каким же?

В данном примере как раз таки здорово выручает формула расстояния между двумя точками на плоскости. Давайте присмотримся к первому уравнению системы:

.

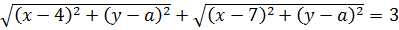
Каждый из корней, фигурирующих в уравнении, очень похож на формулу расстояния между некими точками. Это намёк.) Займёмся расшифровкой каждого корня.

Сопоставим первый корень с выведенной только что формулой расстояния:

.

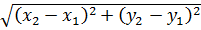
Просто присматриваемся к этим двум корням и сравниваем. Похожи ведь, правда? Тогда, согласно нашей формуле расстояния, можно принять:

Значит, первый корень — это на самом деле расстояние от точки (4; a) до точки (x; y).

Аналогично сопоставив с формулой второй корень, увидим, что он тоже представляет собой расстояние от точки (7; a) опять же до точки (x; y).

А теперь переведём первое уравнение с алгебраического языка (языка формул) на геометрический (язык расстояний).

Сумма расстояний от точки (x; y) до точек (4; a) и (7; a) равна трём.

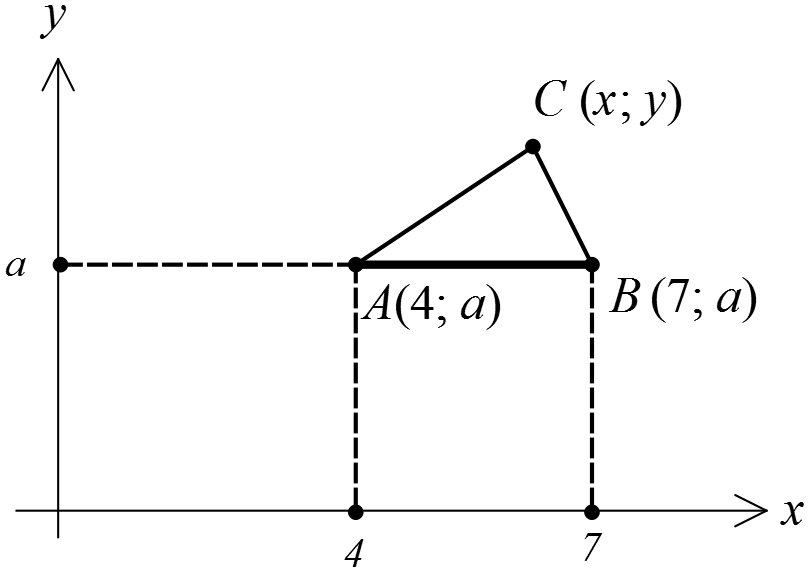
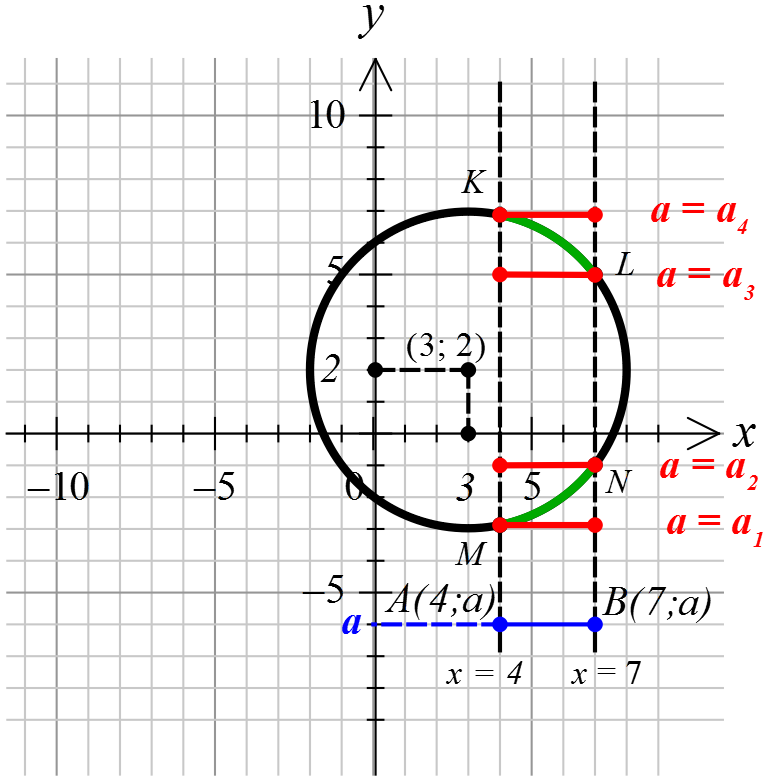
Для наглядности нарисуем картинку, чтобы представлять, а чего, собственно, от нас хотят.)

Значит, согласно рисунку, с геометрической точки зрения первое уравнение системы выглядит так:

где точки А и В зафиксированы (для конкретного значения параметра), а третья точка С как-то «гуляет» по координатной плоскости.

Вообще говоря, множество точек плоскости, сумма расстояний от которых до двух фиксированных точек постоянна и равна некому положительному числу, представляет собой замкнутую кривую, которая называется красивым словом эллипс, а данные фиксированные точки являются фокусами эллипса. Но проблема состоит в том, что понятие эллипса не входит в школьную программу (зачастую даже физико-математических классов), а изучается уже в ВУЗе в курсе аналитической геометрии.) Так как же обойти это незнакомое (пока) понятие? Может, в данной (и подобных этой) задаче всё гораздо проще?

Вынужден признаться. Да, всё гораздо проще!

Дело всё в том, что понятие эллипса справедливо только в том случае, если эта самая сумма расстояний будет больше расстояния между самими фиксированными точками. Если же сумма расстояний от точки С(x; y) до двух фиксированных точек (в данном случае A и B) точно равна расстоянию AB между ними, то точка С(x; y) обязательно будет лежать на отрезке AB, и никакого эллипса уже не будет, а будет просто отрезок AB с «гуляющей» по нему третьей точкой.

Давайте посмотрим, чему же равно расстояние между нашими фиксированными точками:

.

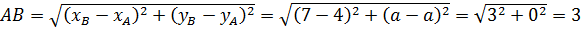
Итак, длина отрезка АВ в точности получилась равной трём, как и правая часть уравнения. Это не случайно!) Что это означает? Это означает то, что наша точка С(x; y) обязательно лежит на отрезке AB и как-то по нему гуляет.) И только на отрезке! Ведь в противном случае, если бы точка С лежала где-то за его пределами (скажем, где-то выше или где-то ниже), то сумма расстояний от неё до концов отрезка АВ была бы строго больше тройки, что противоречило бы первому уравнению.

Что ещё важного можно заметить в данном уравнении и на рисунке? А то, что при любом значении параметра «а» игрековые координаты А и В концов нашего отрезка совпадают (обе равны а). Это означает, что в любом случае наш отрезок АВ будет строго горизонтален (то бишь, параллелен оси ОХ), а его концы, в зависимости от значения параметра, будут как бы скользить вдоль направляющих прямых x=4 и x=7 (поскольку абсциссы его концов никак не зависят от «а», оставаясь всё время равными 4 и 7).

Итак, первое уравнение разложили по полочкам, переходим ко второму.

Вот тут возведение обеих частей в квадрат вполне прокатит. Возводим:

Ну как, знакомо? Да, это классическое уравнение окружности с центром в точке (3;2) и радиусом 5.

Кстати сказать, а как понять, что второе уравнение задаёт именно окружность не через возведение в квадрат, а через расстояние между точками? Снова переводим второе уравнение с алгебры на геометрию, используя нашу формулу расстояния.

Расстояние от точки (x;y) до точки (3;2) равно пяти.

А что же это за множество точек, находящихся от фиксированной точки (3;2) на расстоянии 5? Ну, конечно! Окружность радиуса 5 с центром в данной точке. 🙂

Что ж, у нас уже имеется всё необходимое, чтобы нарисовать общий чертёж к задаче. Поехали!

1) Итак, сначала, как водится, чертим координатные оси X и Y.

2) Проводим пунктиром вспомогательные вертикальные прямые x=4 и x=7. Вдоль этих прямых, в зависимости от параметра «а», будет скользить наш отрезок АВ, всё время оставаясь горизонтальным. Как вагонная ось катится по рельсам.))

3) Отмечаем точку (3; 2) — центр нашей окружности.

4) Собственно, рисуем саму окружность с центром в данной точке и радиусом — пятёрка.

5) Готово! Что в конечном итоге получилось — смотрим рисунок ниже.

А теперь пора рассуждать и включать воображение.) В задаче от нас требуется, чтобы система имела хотя бы одно решение. Что это означает с точки зрения нашего рисунка? А то, что наши отрезок (первое уравнение) и окружность (второе уравнение) должны иметь хотя бы одну общую точку. Когда такое возможно?

Имеем четыре граничные ситуации.

Итак, можно даже составить заготовку для будущего ответа:

.

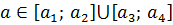
Причём граничные значения параметра а нас тоже устраивают, посему все скобки квадратные.

Что ж, остаются сущие пустяки — определить эти самые граничные значения параметра.)

Начнём с левого конца отрезка. То есть, точки А(4; a). Подставим координаты точки А в уравнение окружности (ведь мы же как раз отлавливаем пересечение отрезка с окружностью!):

Получили два значения параметра. Очевидно, знак минус соответствует крайнему нижнему положению отрезка при a = a₁, а знак плюс — крайнему верхнему при а = а₄. Таким образом,

Аналогично расправляемся и с правым концом — с точкой B(7; a):

Всё! Все интересующие нас значения параметра найдены, и теперь можно с чистой совестью записывать окончательный ответ.)

.

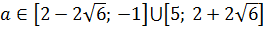
В рассмотренном примере формула расстояния между точками была подана на блюдечке прослеживалась довольно явно. А вот следующий пример будет гораздо сложнее. Там, во-первых, в нагрузку добавятся модули, а во-вторых, потребуются дополнительные преобразования. Но ничего, мы тоже его распутаем.)

Пример 2

Во, накрутили… Сумма корней, под корнями модули… Кошмар!

Как здесь можно узнать формулу расстояния между точками? Ясно, что надо как-то преобразовывать и приводить к красивому виду первое уравнение.

Посмотрим, что получается под первым корнем. Раскроем скобки:

А вот второй корень сразу так красиво преобразовать не выйдет: ведь там у нас совсем нет икса в квадрате, а вместо этого затесался параметр а, да ещё и игрек в первой степени. Чтобы избавиться от а и y, воспользуемся вторым уравнением и подставим в первое уравнение вместо y выражение x 2 +a:

Вот так. И теперь первое уравнение системы стало выглядеть гораздо симпатичнее:

Уже потихоньку вырисовывается нечто знакомое, правда? Что делать дальше? Ясно, что надо раскрывать модули. Лучше, когда их нет.) Давайте начнём с первого корня, то есть с икса.

Если x≥0, то модуль раскрывается с плюсом (|x| = x), и тогда

Таким образом, если x≥0, то первый корень представляет собой расстояние между точками (x; y) и (3; 0). С какой такой стати? Элементарно!

Ведь можно же записать данное выражение вот так:

Точно так же, раскрывая модуль игрека во втором радикале, получим:

Значит, первое уравнение нашей системы разбивается на четыре случая раскрытия модулей:

Каждое из полученных четырёх уравнений выражает сумму расстояний от неких двух фиксированных точек плоскости ОXY до точки (x; y), «гуляющей» где-то по плоскости. И эта сумма расстояний у нас постоянна и равна пяти.

Здесь опять таки не будем выпендриваться и сделаем вид, что понятия не имеем про эллипс, а вместо этого снова посчитаем расстояния между точками.)

Теперь подробно рассмотрим, к примеру, первый случай:

Он представляет собой сумму расстояний от точки (x; y) до точек A и B.

Вычислим длину отрезка АВ из треугольника AOB:

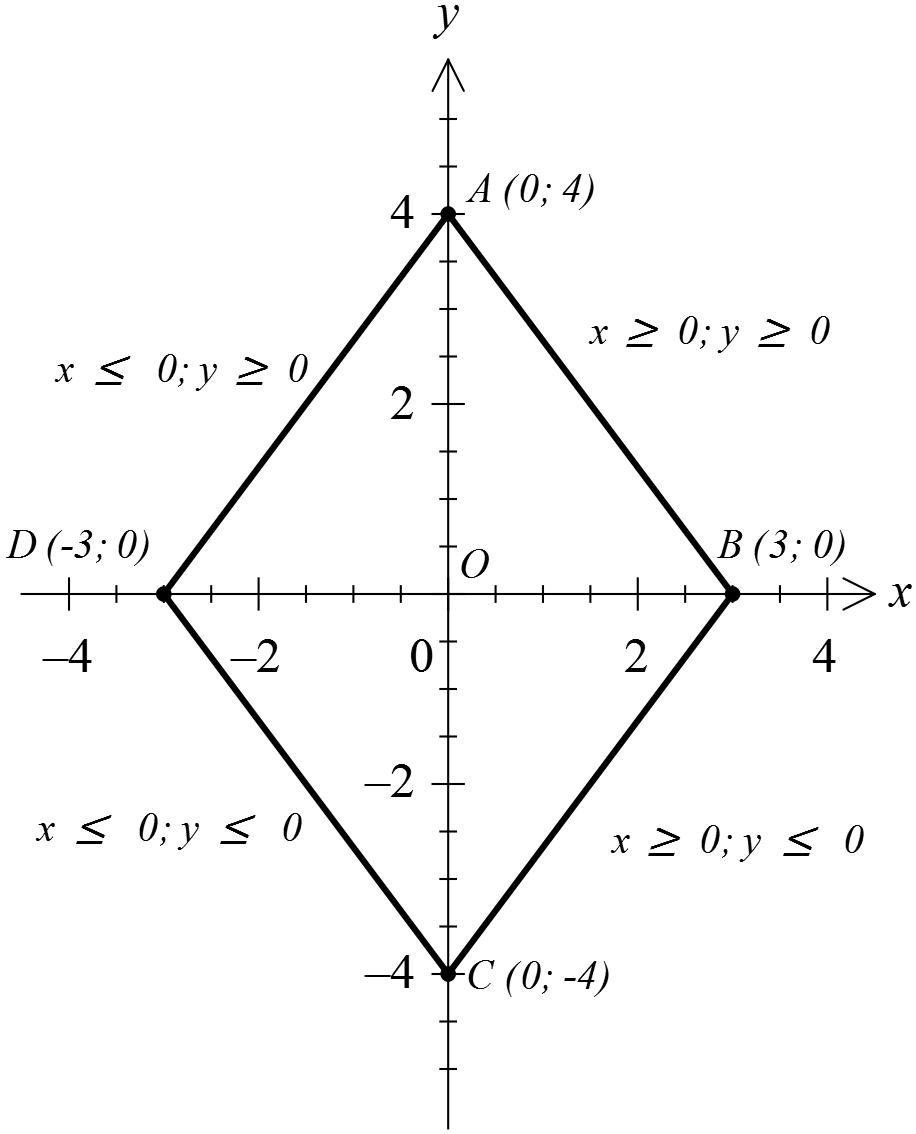
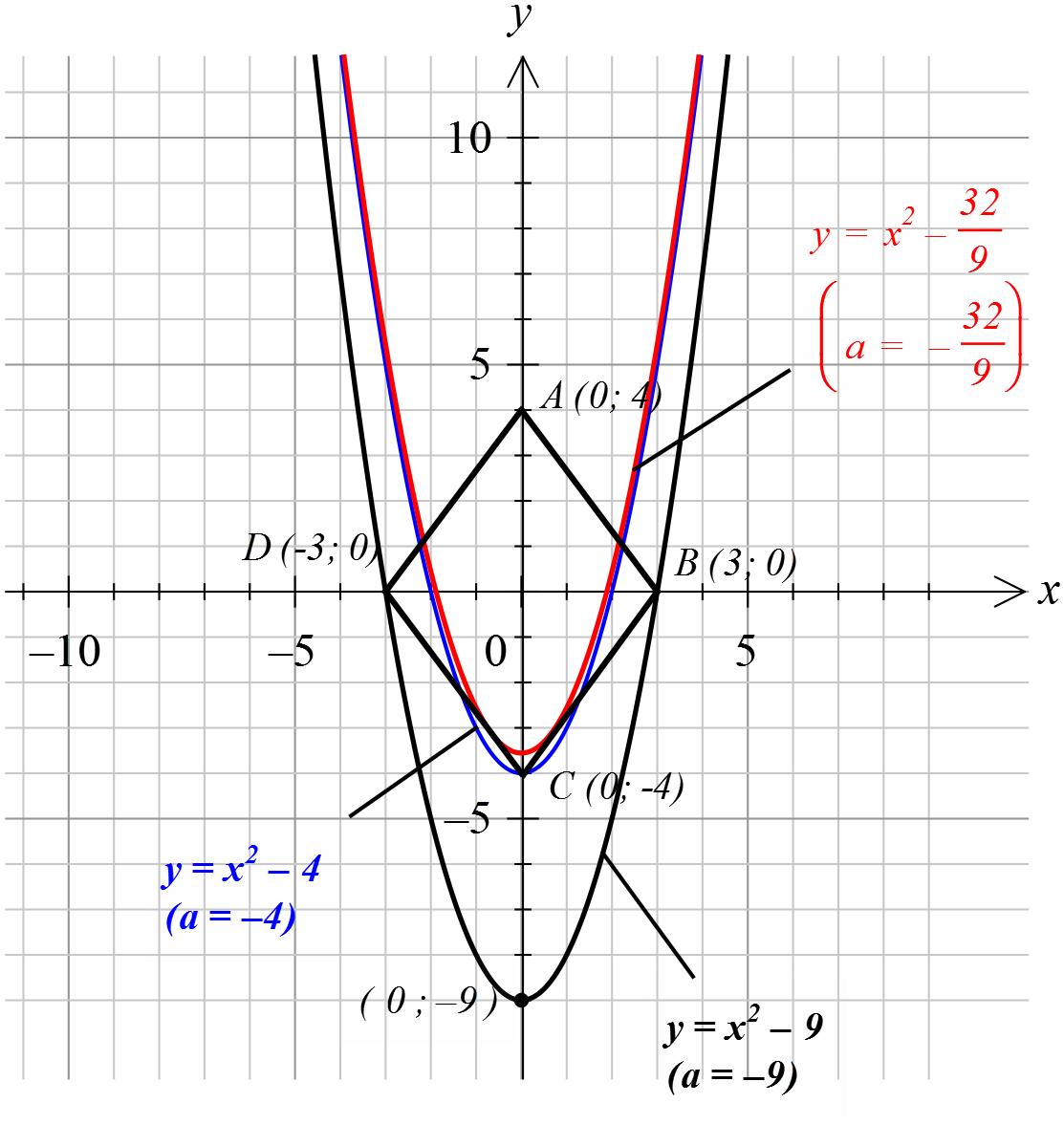
Получили в точности пятёрку. То есть, длину отрезка AB! Что это означает? Это означает, что наша точка с координатами (x; y) обязательно лежит на отрезке АВ и как-то по нему гуляет! Таким же образом доказывается, что и в остальных трёх случаях точка (x; y) лежит на соответствующем отрезке. Итак, множество точек, описывающих первое уравнение системы, — ромб ABCD со стороной 5. Каждая сторона ромба отвечает за свой случай раскрытия модулей.

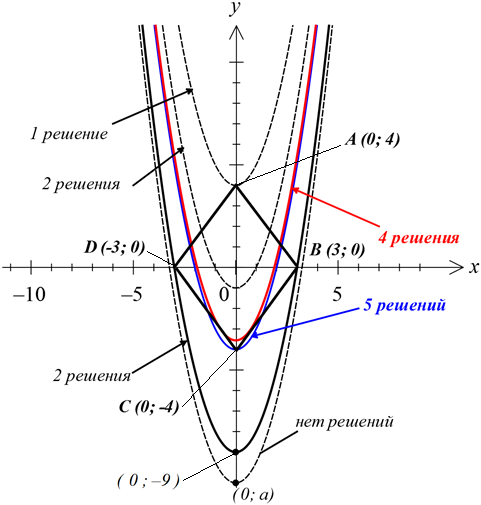
А вот второе уравнение нашей системы — обычная парабола y = x 2 с вершиной в точке (0; a), гуляющая вверх-вниз вдоль оси игреков в зависимости от параметра. Вот наша картинка:

А теперь (внимание!) начинаем двигать нашу параболу снизу вверх вдоль оси OY, меняя тем самым параметр а!

Таким образом, первая часть ответа будет такая:

.

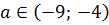
Сами границы нас не устраивают и в ответ, естественно, не включаются.

Но… Это ещё не всё!) Продолжим дальше двигать вверх по оси ОY нашу параболу. Когда вершина окажется чуть выше точки С, то пересечений станет уже шесть: по два с нижними сторонами ромба и по одному с верхними. И так будет до тех пор, пока ветви параболы не станут касаться сторон CD и CB ромба (красный цвет). В случае касания решений снова станет четыре, что от нас и требуется. И это значение параметра а, при котором парабола касается нижних сторон ромба, теперь нам и предстоит «отловить».)

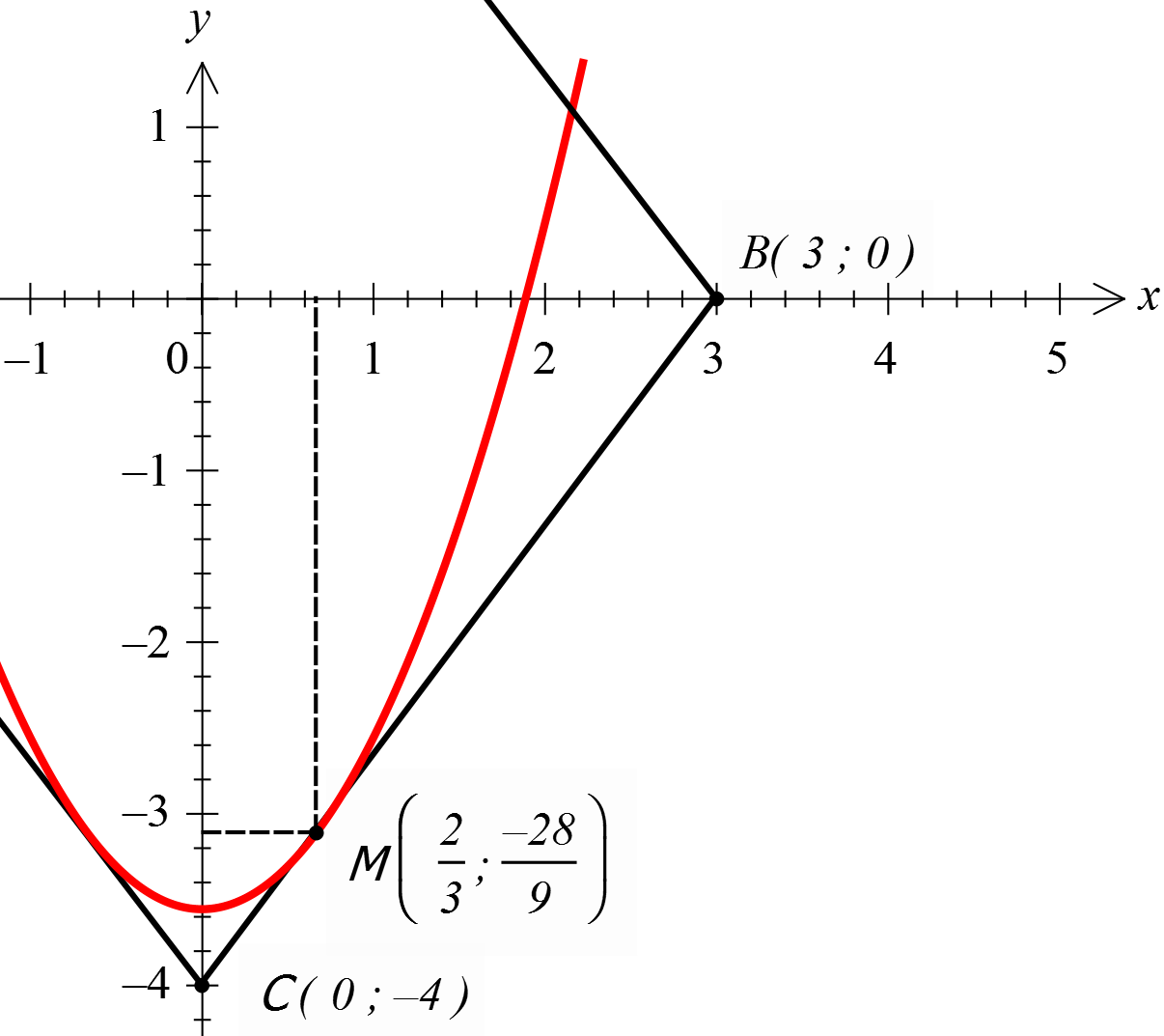
На помощь придёт такой мощный инструмент, как производная. В силу симметрии картинки, рассматривать будем только правую ветвь параболы. Итак, пусть наша красная парабола касается нижнего отрезка ромба СВ в какой-то точке М.

Уравнение прямой, задающей отрезок СВ, будет

поскольку тангенс угла наклона прямой CB к оси ОХ равен:

Уравнение нашей параболы будет y = x 2 + a. Мы не знаем пока, чему равно «а», но зато твёрдо знаем, что отрезок CB её касается, а значит, производная нашей параболы в точке касания M должна быть равна 4/3.

Вычислим эту самую производную:

Поскольку точка M лежит на отрезке CB, то её координаты обязательно удовлетворяют уравнению этого отрезка:

Значит, координаты нашей точки касания следующие:

Но! Точка M принадлежит не только отрезку, но ещё и параболе! Поэтому, подставив координаты точки M в уравнение параболы, мы теперь уже без труда найдём интересующее нас значение а:

Вот теперь всё. Все характерные положения параболы представлены на картинке.

Легко видеть, что при дальнейшем росте параметра а четырёх решений уже не будет, а будет либо два, либо одно, либо ни одного.

Кстати сказать, а можно ли в данной ситуации обойтись без производной? Уж больно напряжно с ней возиться, как правило…

Что ж, специально для разумных халявщиков предлагаю способ-лайт.) Но, следует предупредить, что он срабатывает только в случае каких-нибудь простеньких графиков — в основном для параболы. В случае более сложных функций способ с производной — самый надёжный.)

Итак, нам требуется отыскать значение параметра, при котором происходит касание прямой

.

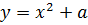
Что означает сей факт с алгебраической точки зрения? Только то, что уравнение

имеет строго один корень! То есть, дискриминант получившегося квадратного уравнения обязан быть равен нулю!

Что ж, остаётся только привести наше уравнение к стандартному виду, посчитать дискриминант да приравнять его к нулю.) Действуем:

Как и следовало ожидать, результат получился тем же самым.)

Заключение: если в примере предложено какое-то зверское на вид уравнение или неравенство с корнями, но подкоренные выражения представляют собой какие-то квадратичные конструкции от x и y вида

то ни в коем случае не возводим обе части в квадрат с целью избавиться от корней и не тратим своё время! Вместо этого пробуем выделить полные квадраты под корнями по каждой из переменных.

Очень часто в таких конструкциях срабатывает именно формула расстояния между двумя точками, что значительно упрощает дальнейшее решение примера и тем самым открывает дорогу к успеху.

Источник