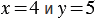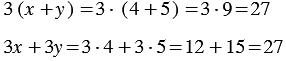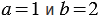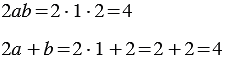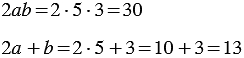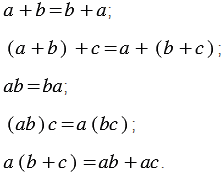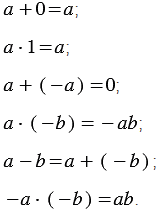Докажите что равенство является тождеством номер 73
Доказательство тождеств
Презентация к уроку
Цели:
Ход урока
Перед началом урока учащиеся класса разбиваются на шесть учебных групп смешанного состава.
Учитель: Здравствуйте, ребята, я предлагаю учебный кабинет превратить на время в научно-исследовательскую лабораторию, а нам с вами в ученых-магистров математических наук.
Но каждый, уважающий себя ученый, постоянно решает какую-нибудь очень важную проблему, вот и нам, прежде всего, предстоит узнать: над какой проблемой мы будем сегодня работать?
Для этого нам нужно решить две задачи: (Слайд 1)
Учитель: Работать сегодня мы будем над «Доказательством тождеств», а девизом нашей работы я предлагаю взять вот эти замечательные слова: (Слайд 2)
Пусть каждый день и каждый час
Нам новое добудет,
Пусть добрым будет ум у нас,
А сердце умным будет!
Учитель: Господа ученые, прежде чем решать поставленную задачу, нам необходимо укрепить свою теоретическую базу, ведь понятие тождества вам уже знакомо. И поэтому в рубрике (Слайд 3) «Повторение – мать учения» я предлагаю вам провести следующую работу:
В каждой научной группе находятся формулировки трех понятий на карточке 1, вы должны среди них найти два определения: 1) Определение тождества, 2) Определение тождественно равных выражений.
(Учащиеся в течение 2-3 минут изучают эти определения, спрашиваются представители тех групп, которые быстрее всех справились с заданием, остальные участники других групп показывают согласие или несогласие с помощью сигнальных карточек зеленого и красного цветов)
Карточка 1
| … – это равенство, верное при любых допустимых значениях, входящих в его состав переменных. |
| Два выражения, соответственные значения которых равны при любых значениях переменных, называются … равными. |
| Замену одного выражения другим, тождественно равным ему, называют … преобразованием выражения. |
После того как учащиеся дают верное определение, оно высвечивается на экране.
Учитель: Хорошо, а сейчас проверим себя. На экране будут появляться равенства, если это равенство будет являться тождеством, то я предлагаю вам встать, если же – нет, то вы продолжаете сидеть: (Слайд 4)
Учитель: Хорошо, а сейчас пришла пора из теоретиков нам превращаться в ученых- практиков, но для этого нам нужно узнать, что нужно использовать, чтобы доказать тождество, и здесь нам не обойтись без научной литературы, ответ на этот вопрос мы найдем на странице … вашего учебника. Учащиеся находят в учебнике ответ: «Чтобы доказать, что некоторое равенство является тождеством, или, как говорят иначе, чтобы доказать тождество, используют тождественные преобразования выражений». Согласие или несогласие участники остальных групп показывают специальными сигналами, о которых говорилось выше. (Слайд 5)
Учитель: Молодцы, но теперь возникает следующий вопрос, а что такое тождественное преобразование выражений? Ответ можно найти на карточке 1, это оставшееся третье определение.
«Замену одного выражения другим, тождественно равным ему, называют тождественным преобразованием выражения» (учитель предлагает ответить на этот вопрос одного из участников любой группы) (Слайд 6)
Вот сейчас мы уже «созрели» для практической работы, и я попрошу вас обратить свое внимание на карточку 2. Задание: «Докажите тождество», каждая группа ученых получила пример, который она должна решить самостоятельно, если будут возникать затруднения на помощь придут карточки- консультанты.
Карточка 2
| Докажите тождество | |
| 1. 10х–(5х+4)=5х–4 | Карточка-консультант |
| Выпишите выражение в левой части указанного равенства, раскрой те скобки и приведите подобные слагаемые, сравните полученное выражение с выражением правой части, сделайте вывод. | |
Карточка 2
| Докажите тождество | |
| 2. 5х – 7 = 28х – 3 – х – 4 – 22х | Карточка-консультант |
| Выпишите выражение правой части указанного равенства, приведите подобные слагаемые, сравните полученное выражение с выражением левой части и сделайте вывод. | |
Карточка 2
| Докажите тождество | |
| 3. (х – 5)(х + 2) = (х + 4)(х – 7) + 18 | Карточка-консультант |
| Выпишите сначала выражение левой части, раскрой те скобки и приведите подобные слагаемые, затем выпишите выражение правой части, раскройте скобки и приведите подобные слагаемые. Сравните полученные выражения, сделайте вывод. | |
Карточка 2
| Докажите тождество | |
| 4. –(2х – 3) + (х 2 + 2х – 3) = х 2 | Карточка-консультант |
| Выпишите выражение в левой части указанного равенства, раскрой те скобки и приведите подобные слагаемые, сравните полученное выражение с выражением правой части, сделайте вывод. | |
Карточка 2
| Докажите тождество | |
| 5. 11х – 3 = 2х + 12 + 9х – 15 | Карточка-консультант |
| Выпишите выражение правой части указанного равенства, приведите подобные слагаемые, сравните полученное выражение с выражением левой части и сделайте вывод. | |
Карточка 2
| Докажите тождество | |
| 6. –4(3у – 1) + 1 = –6(2у – 1) – 1 | Карточка-консультант |
| Выпишите сначала выражение левой части, раскрой те скобки и приведите подобные слагаемые, затем выпишите выражение правой части, раскройте скобки и приведите подобные слагаемые. Сравните полученные выражения, сделайте вывод. | |
Теперь нам необходимо защитить свои работы. (Презентация выполненных работ у доски, выступают желающие участники групп)
Учитель: Замечательно, а теперь уважаемые коллеги пора подводить итоги, что же нам необходимо сделать, чтобы доказать, что равенство является тождеством? Предполагаемые ответы учащихся: (Слайд 7)
Учитель: Какой вывод можно сделать в том случае, когда все то, о чем мы только что сказали, не будет выполняться? Предполагаемый ответ учащихся: Равенство не будет являться тождеством.
Учитель: Чтобы полученные знания были прочными, эту работу мы продолжим дома:
Домашнее задание: п. 30, 773, * Составить равенство, которое будет являться тождеством.
Учитель: А сейчас настал час для творчества: В стихотворении, которое вы видите, вставьте пропущенные слова: (Слайды 8-9)
Равенства всякие, братцы, бывают,
И каждый об этом, конечно же, знает.
Есть – с переменными, есть – (числовые),
Сложные очень и очень (простые),
Но есть среди равенств особенный класс,
О нем поведем свой рассказ мы сейчас.
(Тождеством) равенство это зовется.
Но это еще доказать нам придется.
Для этого нужно нам только лишь взять
И равенство это (преобразовать)
Несложно, конечно, нам будет узнать
Какую придется нам часть изменять,
А, может, придется нам обе менять,
По равенства виду нетрудно (понять)
Ура! Удалось применить наши знания,
Окончено равенства преобразование.
И смело уже говорим мы ответ:
Так (тождество) это, или все-таки нет!
Тождественно равные выражения. Тождества
| Два выражения, значения которых равны при любых значениях переменных, называют тождественно равными. |
Рассмотрим две пары выражений:
1) 
Найдем их значения при
Мы получили один и тот же результат. Из распределительного свойства следует, что вообще при любых значениях переменных 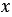
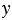

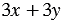
2)
Найдем их значения при
Мы получили один и тот же результат. Однако, можно указать такие значения 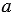
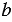
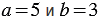
Мы получили разные результаты.
Следовательно, выражения 
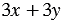
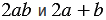
| Равенство, верное при любых значениях переменных, называется тождеством. |
Равенство 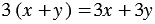
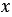
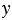
Также к тождествам можно отнести равенства, выражающие свойства сложения и умножения чисел:
Можно привести и другие примеры тождеств:
Тождествами считают и верные числовые равенства.
Очень часто при вычислении значений выражений, легче сначала упростить имеющееся выражение, а затем выполнять вычисления.
| Замену одного выражения другим, тождественно равным ему выражением, называют тождественным преобразованием или просто преобразованием выражения. |
К тождественным преобразованиям можно отнести приведение подобных слагаемых и раскрытие скобок.
Примеры:
1) 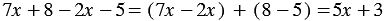
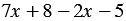
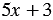
2) 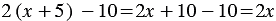
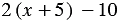
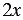
Для того, чтобы доказать, что данное равенство является тождеством (или доказать тождество), используют следующие методы:
1) тождественно преобразуют одну из частей данного равенства, получая другую часть;
2) тождественно преобразуют каждую из частей данного равенства, получая одно и то же выражение;
3) доказывают, что разность левой и правой частей данного равенства тождественно равна нулю.
Также, чтобы доказать, что равенство не является тождеством, достаточно привести контрпример, т.е. указать такое значение переменной (или переменных, если их несколько), при котором данное равенство не выполняется.
Пример: Докажите, что равенство 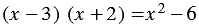
Решение: Приведем контрпример. Если 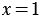
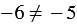
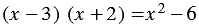
Поделись с друзьями в социальных сетях:
Лекция №3. Доказательство тождеств
ЛЕКЦИЯ №3 Доказательство тождеств
Цель: 1. Повторить определения тождества и тождественно равных выражений.
2.Ввести понятие тождественного преобразования выражений.
3. Умножение многочлена на многочлен.
4. Разложение многочлена на множители способом группировки.
Пусть каждый день и каждый час
Пусть добрым будет ум у нас,
А сердце умным будет!
В математике существует множество понятий. Одно из них тождество.
Тождеством называют равенство, которое выполняется при всех значениях переменных, которые в него входят. Некоторые тождества мы уже знаем.
Например, все формулы сокращенного умножения являются тождествами.
Формулы сокращенного умножения
4. a3 ± b3 = (a ± b)(a2 
Доказать тождество – это значит установить, что для любого допустимого значение переменные его левая часть равна правой части.
В алгебре существует несколько различных способов доказательства тождеств.
Способы доказательства тождеств
- Выполнить равносильные преобразования левой части тождества. Если в итоге получим правую часть, тогда тождество считается доказанным. Выполнить равносильные преобразования правой части тождества. Если в итоге получим левую часть, тогда тождество считается доказанным. Выполнить равносильные преобразования левой и правой части тождества. Если в результате получим одинаковый результат, тогда тождество считается доказанным. Из правой части тождества вычитаем левую часть. Производим над разностью равносильные преобразования. И если в итоге получаем нуль, то тождество считается доказанным. Из левой части тождества вычитают правую часть. Производим над разностью равносильные преобразования. И если в итоге получаем нуль, то тождество считается доказанным.
Следует так же помнить, что тождество справедливо лишь для допустимых значений переменных.
Как видите способов достаточно много. Какой способ выбрать в данном конкретном случае, зависит от тождества, которое вам необходимо доказать. По мере того, как вы будете доказывать различные тождества, придет и опыт в выборе способа доказательства.
Пример 1. Докажите тождество x·(a+b) + a·(b-x) = b·(a+x).
Так как в правой части небольшое выражение, попытаемся преобразовать левую часть равенства.
x·(a+b) + a·(b-x) = x·a +x·b + a·b – a·x.
Приведем подобные слагаемые и вынесем общий множитель за скобку.
x·a + x·b + a·b – a·x = x·b + a·b = b·(a + x).
Получили что левая часть после преобразований, стала такой же как и правая часть. Следовательно, данное равенство является тождеством.
В данном примере можно поступить следующим способом. Раскроем скобки в правой части равенства.
(a+5)·(a+2) = (a²) + 5·a +2·a +10 = a²+7·a + 10.
Видим, что после преобразований, правая часть равенства стала такой же как и левая часть равенства. Следовательно, данное равенство является тождеством.
« Замену одного выражения другим, тождественно равным ему, называют тождественным преобразованием выражения»
Выяснить какое равенство является тождеством:
«Чтобы доказать, что некоторое равенство является тождеством, или, как говорят иначе, чтобы доказать тождество, используют тождественные преобразования выражений»
Умножение многочлена на многочлен
Умножим многочлен a + b на многочлен c + d. Составим произведение этих многочленов:
(a+b)(c+d).
Обозначим двучлен a + b буквой x и преобразуем полученное произведение по правилу умножения одночлена на многочлен:
(a+b)(c+d) = x(c+d) = xc + xd.
В выражение xc + xd. подставим вместо x многочлен a+b и снова воспользуемся правилом умножения одночлена на многочлен:
xc + xd = (a+b)c + (a+b)d = ac + bc + ad + bd.
Итак: (a+b)(c+d) = ac + bc + ad + bd.
Произведение многочленов a + b и c + d мы представили в виде многочлена ac + bc + ad + bd. Этот многочлен является суммой всех одночленов, получающихся при умножении каждого члена многочлена a + b на каждый член многочлена c + d.
Вывод: произведение любых двух многочленов можно представить в виде многочлена.
Правило: чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить.
Заметим, что при умножении многочлена, содержащего m членов на многочлен, содержащий n членов в произведении до приведения подобных членов должно получиться mn членов. Этим можно воспользоваться для контроля.
Разложение многочлена на множители способом группировки:
1. Способы доказательства тождеств.
2. Что называют тождественным преобразованием выражения.
3. Умножение многочлена на многочлен.
4. Разложение многочлена на множители способом группировки