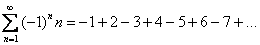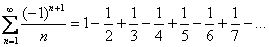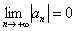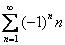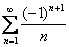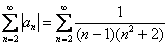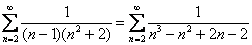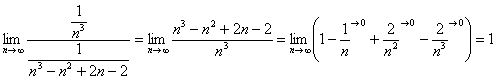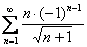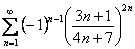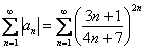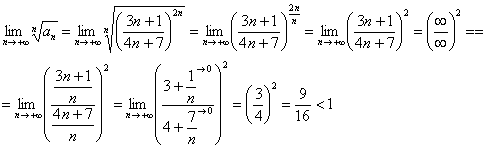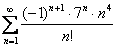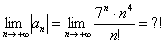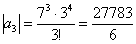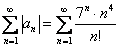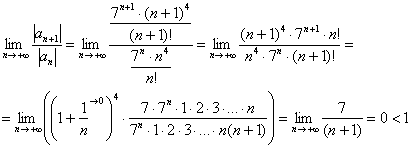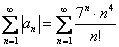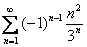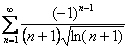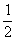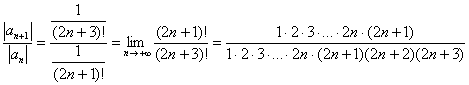Докажите что ряд расходится

Числовые ряды: определения, свойства, признаки сходимости, примеры, решения

Данная статья представляет собой структурированную и подробную информацию, которая может пригодиться во время разбора упражнений и задач. Мы рассмотрим тему числовых рядов.

Данная статья начинается с основных определений и понятий. Далее мы стандартные варианты и изучим основные формулы. Для того, чтобы закрепить материал, в статье приведены основные примеры и задачи.

Базовые тезисы

a k является общим или k –ым членом ряда.

Определения, рассмотренные выше, помогут вам для решения большинства примеров и задач.

Для того, чтобы дополнить определения, необходимо доказать определенные уравнения.

Мы доказали, что числовой ряд сходится.

Мы доказали, что числовой ряд расходится.

Ряд ∑ k = 1 ∞ b k знакопеременный, так как в нем множество чисел, отрицательных и положительных.

Второй вариант ряд – это частный случай третьего варианта.

Приведем примеры для каждого случая соответственно:

Для третьего варианта также можно определить абсолютную и условную сходимость.

Знакочередующийся ряд ∑ k = 1 ∞ b k абсолютно сходится в том случае, когда ∑ k = 1 ∞ b k также считается сходящимся.

Подробно разберем несколько характерных вариантов

Знакопеременный ряд ∑ k = 1 ∞ b k считается условно сходящимся в том случае, если ∑ k = 1 ∞ b k – расходящийся, а ряд ∑ k = 1 ∞ b k считается сходящимся.

Особенности сходящихся рядов

Проанализируем свойства для определенных случаев

Разложим исходный вариант:

Необходимое условие для определения, является ли ряд сходящимся

Проверим исходное выражение на выполнение условия lim n → + ∞ n 2 1 + n = lim n → + ∞ n 2 n 2 1 n 2 + 1 n = lim n → + ∞ 1 1 n 2 + 1 n = 1 + 0 + 0 = + ∞ ≠ 0

Как определить сходимость знакоположительного ряда.

Если постоянно пользоваться указанными признаками, придется постоянно вычислять пределы. Данный раздел поможет избежать сложностей во время решения примеров и задач. Для того, чтобы определить сходимость знакоположительного ряда, существует определенное условие.

Как сравнивать ряды

Существует несколько признаков сравнения рядов. Мы сравниваем ряд, сходимость которого предлагается определить, с тем рядом, сходимость которого известна.

Первый признак

Для того, чтобы закрепить полученный материал, детально рассмотрим пару типичных вариантов.

Второй признак

Согласно второму признаку можно определить, что сходящийся ряд ∑ k = 1 ∞ 1 k 3 означается, что первоначальный вариант также сходится.

Согласно приведенным выше тезисам, расходящийся ряд влечет собой расходимость исходного ряда.

Третий признак

Рассмотрим третий признак сравнения.

Признак Даламбера

Признак Даламбера справедлив в том случае, если предел бесконечен.

Определить, является ряд сходящимся или расходящимся ∑ k = 1 ∞ 2 k + 1 2 k по признаку Даламбера.

Необходимо проверить, выполняется ли необходимое условие сходимости. Вычислим предел, воспользовавшись правилом Лопиталя: lim k → + ∞ 2 k + 1 2 k = » open=» ∞ ∞ = lim k → + ∞ 2 k + 1 ‘ 2 k ‘ = lim k → + ∞ 2 2 k · ln 2 = 2 + ∞ · ln 2 = 0

Мы можем увидеть, что условие выполняется. Воспользуемся признаком Даламбера: lim k → + ∞ = lim k → + ∞ 2 ( k + 1 ) + 1 2 k + 1 2 k + 1 2 k = 1 2 lim k → + ∞ 2 k + 3 2 k + 1 = 1 2 1

Ряд является сходящимся.

Следовательно, ряд является расходящимся.

Радикальный признак Коши

Данный признак может быть использован в примерах, которые легко определить. Случай будет характерным тогда, когда член числового ряда – это показательно степенное выражение.

Для того, чтобы закрепить полученную информацию, рассмотрим несколько характерных примеров.

Определить, является ли знакоположительный ряд ∑ k = 1 ∞ 1 ( 2 k + 1 ) k на сходящимся.

Интегральный признак Коши

, то в случае, если несобственный интеграл ∫ a + ∞ f ( x ) d x является сходящимся, то рассматриваемый ряд также сходится. Если же он расходится, то в рассматриваемом примере ряд тоже расходится.

При проверке убывания функции можно использовать материал, рассмотренный на предыдущих уроках.

Рассмотреть пример ∑ k = 2 ∞ 1 k · ln k на сходимость.

Согласно полученным результатам, исходный пример расходится, так как несобственный интеграл является расходящимся.

Признак Раабе

Данный способ определения можно использовать в том случае, если описанные выше техники не дают видимых результатов.

Исследование на абсолютную сходимость

Расходимость знакопеременных рядов

Если ряд ∑ k = 1 ∞ b k – расходящийся, то соответствующий знакопеременный ряд ∑ k = 1 ∞ b k либо расходящийся, либо условно сходящийся.

Признаки для условной сходимости

Признак Лейбница

Ряд условно сходится.

Признак Абеля-Дирихле

∑ k = 1 + ∞ u k · v k сходится в том случае, если < u k >не возрастает, а последовательность ∑ k = 1 + ∞ v k ограничена.

Источник

Докажите что ряд расходится

Числовым рядом (или просто рядом) называется бесконечная сумма ви да

где – действительные или комплексные числа, называемые членами ряда, u_n – общим членом ряда.

Если известен общий член ряда как функция его номера n : u_n = f ( n ), то ряд считают заданным.

Рассмотрим последовательность частичных сумм ряда (9.1):

Сформулируем некоторые свойства числовых рядов.

3. Если к ряду (9.1) прибавить или отбросить конечное число членов, то полученный ряд и ряд (9.1) сходятся или расходятся одновременно.

Следствие (достаточное условие расходимости ряда). Если или этот предел не существует, то ряд расходится

Решение. Вычислим предел общего члена ряда:

Во многих случаях на вопрос о сходимости или расходимости числового ряда можно ответить с помощью достаточных признаков.

Сходимость или расходимость знакоположительного ряда часто устанавливается путем сравнения его с другим рядом, о котором известно, сходится он или не т. Подобное сравнение базируется на теоремах 9.2 и 9.3.

Теорема 9.2 (признак сравнения числовых знакоположительных рядов). Пусть даны два знакоположительных ряда

В этом случае ряд (9.4) называется минорантным, а ряд (9.5) – мажорантным рядом.

Теорема 9.3. (признак сравнения в предельной форме)

Примечание. Если l =1, то ряд (9.1) может быть как сходящимся, так и расходящимся

Признак Даламбера целесообразно применять, когда общий член ряда содержит факториалы и показательные выражения.

Теорема 9.5 (радикальный признак Коши). Если для ряда (9.1) с положительными членами существует конечный или бесконечный предел , то при при l 1 ряд сходится и расходится при l > 1

Решение. Учитывая теорему 9.5 и второй замечательный предел (3.13), вычисляем:

Теорема 9.6 (интегральный признак Коши). Если члены знакоположительного числового ряда могут быть представлены как числовые значения некоторой непрерывной монотонно убывающей на промежутке [1;∞) функции f ( x ) так, что u ₁ = f (1), u ₂ = f (2), …, u_n = f ( n ), …, то если сходится, то сходится и ряд (9.1); если расходится, то расходится также и ряд (9.1)

Так как несобственный интеграл от общего члена ряда сходится, то и исходный ряд также сходится (согласно теореме 9.6)

Особое значение в теории числовых рядов (в частности, при их сравнении) имеет обобщенный гармонический ряд

где p > 0 – действительное число. Для исследования ряда (9.6) применим теорему 9.6 (интегральный признак Коши).

Помимо знакоположительных числовых рядов существует важный класс знакопеременных рядов, в которых члены ряда имеют произвольные знаки.

Теорема 9.7 (общий достаточный признак сходимости). Пусть дан знакопеременный ряд

составленный из модулей членов данного ряда, то сходится и сам знакопеременный ряд (9.7)

Знакопеременный ряд называется абсолютно сходящимся, если ряд, составленный из модулей его членов, сходится.

Знакопеременный ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.

Сформулируем основные свойства абсолютно сходящихся рядов.

2. Абсолютно сходящиеся ряды с суммами S ₁ и S ₂ можно почленно складывать (вычитать). В результате получается абсолютно сходящийся ряд, сумма которого равна S ₁ + S ₂ ( S ₁ – S ₂ ).

Примечание. В случае условно сходящихся рядов подобные свойства, вообще говоря, места не имеют.

Используя указанные свойства, математические действия и операции производят только над абсолютно сходящимися рядами. Для установления абсолютной сходимости используют все признаки сходимости знакоположительных рядов, заменяя всюду общий член ряда его модулем.

Частным случаем знакопеременных рядов являются знакочередующиеся ряды, члены которых имеют строго чередующиеся знаки:

Для знакочередующихся рядов имеет место следующий достаточный признак сходимости.

Ряд, членами которого являются функции от переменной x, называется функциональным:

В области сходимости функционального ряда его сумма является некоторой функцией от x : S = S ( x ), которая определяется равенством:

Частным случаем функционального ряда является степенной ряд, члены которого представляют собой степенные функции аргумента x:

Действительные (или комплексные) числа называются коэффициентами ряда (9.11), – действительная переменная.

где x ₀ – некоторое постоянное число.

Рассмотрим вопрос о нахождении области сходимости степенного ряда.

На практике радиус сходимости степенного ряда (9.11) отыскивают с помощью признака Даламбера. Для этого составляют ряд из модулей членов ряда:

и применим к нему признак Даламбера. Допустим, что существует предел

С помощью радикального признака Коши (теоремы 9.5) можно показать, что радиус сходимости также вычисляется по формуле:

Примечание. Интервал сходимости степенного ряда (9.12) находят из неравенства | x – x ₀ | R ; он имеет вид ( x ₀ – R ; x ₀ + R )

Следовательно, данный ряд абсолютно сходится в единственной точке х = 0.

Для нахождения области сходимости ряда применим признак Даламбера:

Данный ряд сходится абсолютно при тех значениях x , которые удовлетворяют неравенству

Исследуем сходимость ряда на концах полученного интервала.

Так как несобственный интеграл сходится, то сходится и исследуемый ряд. Значит, при исходный ряд сходится.

Таким образом, – область сходимости заданного по условию ряда

Источник

Знакочередующиеся ряды. Признак Лейбница.
Абсолютная и условная сходимость

Для того чтобы понять примеры данного урока необходимо хорошо ориентироваться в положительных числовых рядах: понимать, что такое ряд, знать необходимый признак сходимости ряда, уметь применять признаки сравнения, признак Даламбера, признаки Коши. Тему можно поднять практически с нуля, последовательно изучив статьи Ряды для чайников и Признак Даламбера. Признаки Коши. Логически этот урок является третьим по счёту, и он позволит не только разобраться в знакочередующихся рядах, но и закрепить уже пройденный материал! Какой-то новизны будет немного, и освоить знакочередующиеся ряды не составит большого труда. Всё просто и доступно.

Что такое знакочередующийся ряд? Это понятно или почти понятно уже из самого названия. Сразу простейший пример.

Рассмотрим ряд 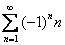и распишем его подробнее:

А сейчас будет убийственный комментарий. У членов знакочередующегося ряда чередуются знаки: плюс, минус, плюс, минус, плюс, минус и т.д. до бесконечности.

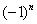
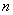
Знакочередование обеспечивает множитель : если чётное, то будет знак «плюс», если нечётное – знак «минус» (как вы помните ещё с урока о числовых последовательностях, эта штуковина называется «мигалкой»). Таким образом, знакочередующийся ряд «опознается» по минус единичке в степени «эн».

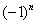
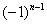
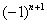
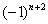
В практических примерах знакочередование членов ряда может обеспечивать не только множитель , но и его родные братья: , , , …. Например:

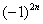
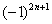
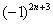
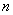
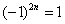
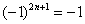
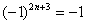
Подводным камнем являются «обманки»: , , и т.п. – такие множители не обеспечивают смену знака. Совершенно понятно, что при любом натуральном : , , . Ряды с обманками подсовывают не только особо одаренным студентам, они время от времени возникают «сами собой» в ходе решения функциональных рядов.

Как исследовать знакочередующийся ряд на сходимость? Использовать признак Лейбница. Про немецкого гиганта мысли Готфрида Вильгельма Лейбница я рассказывать ничего не хочу, так как помимо математических трудов, он накатал несколько томов по философии. Опасно для мозга.

Признак Лейбница: Если члены знакочередующегося ряда монотонно убывают по модулю, то ряд сходится.

1) Ряд является знакочередующимся.

2) Члены ряда убывают по модулю: 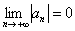, причём, убывают монотонно.

Если выполнены эти условия, то ряд сходится.

Краткая справка о модуле приведена в методичке Горячие формулы школьного курса математики, но для удобства ещё раз:

Что значит «по модулю»? Модуль, как мы помним со школы, «съедает» знак «минус». Вернемся к ряду 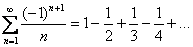. Мысленно сотрём ластиком все знаки и посмотрим на числа. Мы увидим, что каждый следующий член ряда меньше, чем предыдущий. Таким образом, следующие фразы обозначают одно и то же:

– Члены ряда без учёта знака убывают.
– Члены ряда убывают по модулю.
– Члены ряда убывают по абсолютной величине.
– Модуль общего члена ряда стремится к нулю:

// Конец справки

Теперь немного поговорим про монотонность. Монотонность – это скучное постоянство.

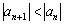
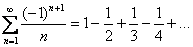
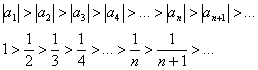
Члены ряда строго монотонно убывают по модулю, если КАЖДЫЙ СЛЕДУЮЩИЙ член ряда по модулю МЕНЬШЕ, чем предыдущий: . Для ряда выполнена строгая монотонность убывания, её можно расписать подробно:

А можно сказать короче: каждый следующий член ряда по модулю меньше, чем предыдущий: .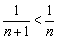

Члены ряда нестрого монотонно убывают по модулю, если КАЖДЫЙ СЛЕДУЮЩИЙ член ряда по модулю НЕ БОЛЬШЕ предыдущего: . Рассмотрим ряд с факториалом: Здесь имеет место нестрогая монотонность, так как первые два члена ряда одинаковы по модулю. То есть, каждый следующий член ряда по модулю не больше предыдущего: .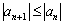

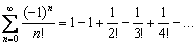
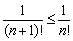
В условиях теоремы Лейбница должна выполняться монотонность убывания (неважно, строгая или нестрогая). Кроме того, члены ряда могут даже некоторое время возрастать по модулю, но «хвост» ряда обязательно должен быть монотонно убывающим.

Не нужно пугаться того, что я нагородил, практические примеры всё расставят по своим местам:

Исследовать ряд на сходимость

В общий член ряда входит множитель 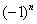, и это наталкивает на естественную мысль проверить выполнение условий признака Лейбница:

1) Проверка ряда на знакочередование. Обычно в этом пункте решения ряд расписывают подробно 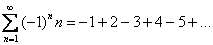и выносят вердикт «Ряд является знакочередующимся».

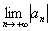
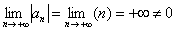
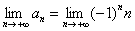
2) Убывают ли члены ряда по модулю? Здесь нужно решить предел , который чаще всего является очень простым.

– члены ряда не убывают по модулю, и из этого автоматически следует его расходимость – по той причине, что предела не существует *, то есть, не выполнен необходимый признак сходимости ряда.

* Согласно, строгому определению предела числовой последовательности, и кроме того, в данном случае это очевидно.

Вывод: ряд расходится.

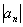
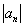
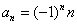
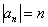
Как разобраться, чему равно ? Очень просто. Как известно, модуль уничтожает минусы, поэтому для того, чтобы составить , нужно просто убрать с крыши проблесковый маячок. В данном случае общий член ряда . Тупо убираем «мигалку»: .

Исследовать ряд на сходимость

Используем признак Лейбница:

1)
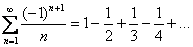
Ряд является знакочередующимся.

2) – члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше, чем предыдущий: () – поскольку бОльшим знаменателям соответствуют мЕньшие дроби. Таким образом, убывание монотонно.

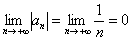
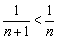
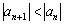
Вывод: ряд сходится.

Однако это еще не всё! Сходимость бывает разной. А именно:

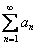
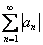
– сходящийся ряд называют абсолютно сходящимся, если сходится ряд ;
в противном случае ряд 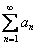сходится условно.

! Из вышесказанного очевидно следует, что любой сходящийся положительный ряд является абсолютно сходящимся.

Составим ряд из модулей – опять просто убираем множитель, который обеспечивает знакочередование:
– расходится (гармонический ряд) – тут даже без исследования обошлось.

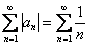
Таким образом, наш ряд 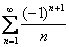сходится условно.

Следует отметить, что при формулировке «Исследуйте ряд на сходимость» можно рискнуть и ограничиться признаком Лейбница (т.е. просто констатировать сходимость), но таки лучше не лениться – с большой вероятностью вас попросят уточнить, сходится ли ряд абсолютно или условно.

Заметьте также, что в Примере 1 второй этап по-любому отпадает, поскольку еще на первом шаге сделан вывод о том, что ряд расходится.

Собираем ведёрки, лопатки, машинки и выходим из песочницы, чтобы смотреть на мир широко открытыми глазами из кабины моего экскаватора:

Исследовать ряд на сходимость

Используем признак Лейбница:

1)
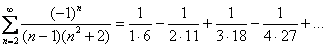
Данный ряд является знакочередующимся.

2) – члены ряда убывают по модулю.

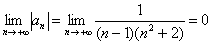
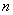
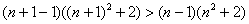
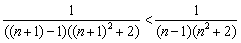
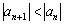
Для любого номера справедливо неравенство: , а бОльшим знаменателям соответствуют меньшие дроби:
, то есть, каждый следующий член ряда по модулю меньше, чем предыдущий: , а это означает, что убывание монотонно.

Вывод: ряд сходится.

Теперь выясним, как именно. Для этого составим и исследуем соответствующий ряд из модулей:

Анализируя начинку, приходим к выводу, что здесь нужно использовать предельный признак сравнения. Скобки в знаменателе удобнее раскрыть:

Сравним данный ряд со сходящимся рядом 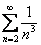. Используем предельный признак сравнения.

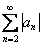
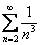
Получено конечное число, отличное от нуля, значит, ряд сходится вместе с рядом .

Таким образом, ряд 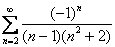сходится абсолютно.

Исследовать ряд на сходимость

Исследовать ряд на сходимость

Это примеры для самостоятельного решения. Полное решение и образец оформления в конце урока.

Как видите, знакочередующиеся ряды – это просто и занудно! Но не спешите закрывать страницу, всего через пару экранов мы рассмотрим случай, который многих ставит в тупик. А пока еще пара примеров для тренировки и повторения.

Исследовать ряд на сходимость

Используем признак Лейбница:

1) Ряд является знакочередующимся.

2) – члены ряда убывают по модулю. Осталось показать монотонность убывания. Неравенство здесь обосновать трудно и поэтому мы проявим разумную хитрость, расписав несколько конкретных членов и всю цепочку:

– не лишним будет взять в руки калькулятор, и убедиться в справедливости первых неравенств (хотя, это, конечно, некорректная проверка).

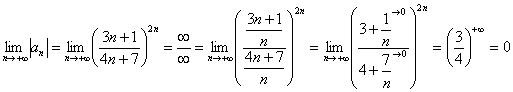
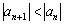
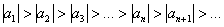
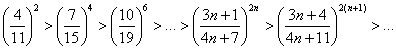
Вывод: ряд сходится.

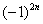
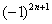
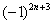
Обратите внимание, что я не расписал подробно члены ряда. Их всегда желательно расписывать, но от непреодолимой лени в «тяжелых» случаях можно ограничиться фразой «Ряд является знакочередующимся». Кстати, не нужно относиться к этому пункту формально, всегда проверяем (хотя бы мысленно) что ряд действительно знакочередуется. Помните об «обманках» , , – если они есть, то от них нужно избавиться, получив «обычный» ряд с положительными членами.

Выясним характер сходимости ряда:

Очевидно, что нужно использовать радикальный признак Коши:

Таким образом, ряд 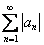сходится.

Исследуемый ряд сходится абсолютно.

Исследовать ряд на сходимость

Это пример для самостоятельного решения. Хммм… что-то я немного погорячился на счет простоты.

Нередко встречаются знакочередующиеся ряды, которые вызывают затруднения.

Исследовать ряд на сходимость

Используем признак Лейбница:

1) Ряд является знакочередующимся.

2)

Дело в том, что не существует стандартных обыденных приемов для решения подобных пределов. Куда стремится такой предел? К нулю, к бесконечности? Здесь важно знать, ЧТО на бесконечности растёт быстрее – числитель или знаменатель.

Примечание: понятие порядка роста функции подробно освещено в статье Методы решения пределов. У нас пределы последовательностей, но это не меняет сути.

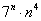
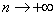
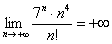
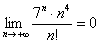
Если числитель при растёт быстрее факториала, то . Если, на бесконечности факториал растёт быстрее числителя, то он, наоборот – «утянет» предел на ноль: . А может быть этот предел равен какому-нибудь отличному от нуля числу?

Попробуем записать несколько первых членов ряда: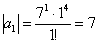

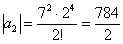
Создается стойкое впечатление, что 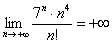, но где гарантия, что при очень больших «эн» факториал не «обгонит» числитель и не утащит предел на ноль?

Обратимся к теории математического анализа, для того она и существует:

Справка:

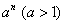
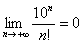
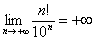
– Факториал растёт быстрее, чем показательная последовательность , иными словами: или . Да хоть миллион в степени «эн», это не меняет дела. То есть, факториал более высокого порядка роста.

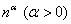
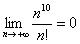
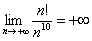
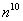
– Факториал растёт быстрее, чем степеннАя последовательность или многочлен, иными словами: или . Вместо можно подставить какой-нибудь многочлен тысячной степени, это опять же не изменит ситуацию – рано или поздно факториал всё равно «перегонит» и такой страшный многочлен. То есть и здесь факториал более высокого порядка роста.

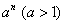
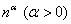
– Факториал растёт быстрее произведения показательной и степенной последовательностей (наш случай). А также быстрее произведения и бОльшего количества таких множителей.

И, раз пошла такая пьянка:

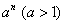
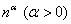
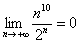
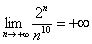
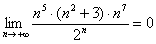
– Показательная последовательность растёт быстрее, чем степенная последовательность , например: , . Аналогично факториалу, она «перетягивает» произведение степенных последовательностей: .

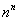
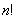
– А есть ли что-нибудь «круче» факториала? Есть! Степенно-показательная последовательность растёт быстрее, чем . На практике встречается редко, но информация лишней не будет.

Таким образом, второй пункт исследования (вы еще о нём помните? =)) можно записать так:
2) – члены ряда монотонно убывают по модулю (так как более высокого порядка роста, чем ).

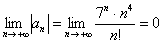
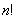
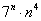
Достаточно! О том, что члены начинают убывать лишь с некоторого номера «эн», лучше благоразумно умолчать – по той причине, что найти этот номер не так-то просто, а лишние вопросы вам ни к чему 😉 Ещё труднее показать монотонность убывания, поэтому просто констатируем этот факт. Здесь вас с высокой вероятностью «простят»

Вывод: ряд сходится.

Исследуем ряд, составленный из модулей членов:

А тут уже работает старый добрый признак Даламбера:

Таким образом, ряд 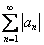сходится.

Исследуемый ряд сходится абсолютно.

Разобранный пример можно решить другим способом.

Теорема: если ряд 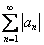сходится, то сходится и ряд

Пример 8 «на бис» вторым способом.

Исследовать ряд на сходимость

Решение: исследуем сходимость ряда, составленного из модулей:

Используем признак Даламбера:
…
только что печатал
…
Таким образом, ряд 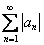сходится, а значит, по соответствующей теореме, сходится и исследуемый ряд, причём, ясно как день – абсолютно.

Вывод: ряд 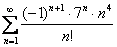сходится абсолютно.

Правда, при втором способе решения есть риск, что преподаватель оценит хитро… смекалку студента и забракует задание. А может и не забракует. Ибо условие не предписывает использовать именно признак Лейбница (но обычно это всё же подразумевается).

И напоследок пара примеров для самостоятельного решения. Один из той же оперы (перечитайте справку), но попроще. Другой для гурманов – на закрепление интегрального признака сходимости.

Исследовать ряд на сходимость

Исследовать ряд на сходимость

После качественной проработки числовых положительных и знакопеременных рядов с чистой совестью можно перейти к функциональным рядам, которые не менее монотонны и однообразны интересны.

Пример 4: Используем признак Лейбница:

1) – данный ряд является знакочередующимся.
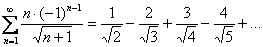
2)

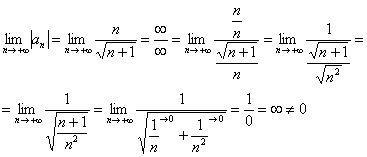
Члены ряда не убывают по модулю, следовательно, предела 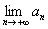не существует, и ряд расходится, т.к. не выполнен необходимый признак сходимости.

Вывод: ряд расходится.
Примечание: в данном примере неопределенность 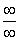устраняется стандартным способом: делением числителя и знаменателя на «эн» в старшей степени. Старшая степень числителя: 1, старшая степень знаменателя:

Пример 5: Используем признак Лейбница.
1) – ряд является знакочередующимся.
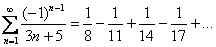
2) – члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше предыдущего: , т.е. убывание монотонно.

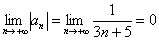
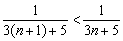
Таким образом, ряд сходится по признаку Лейбница.

С помощью ряда, составленного из модулей, выясним как именно: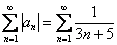

Сравним данный ряд с расходящимся гармоническим рядом . Используем предельный признак сравнения:
– конечное число, отличное от нуля, значит, ряд расходится вместе с гармоническим рядом.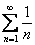
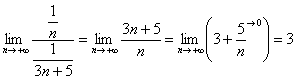
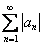
Таким образом, ряд 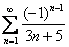сходится условно.

Пример 7: Используем признак Лейбница.
1) – ряд является знакочередующимся.
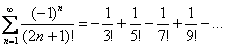
2) – члены ряда убывают по модулю. Найдём модуль -го члена: . Для любого номера справедливо неравенство :

( ), т.е. члены убывают монотонно.

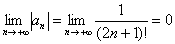
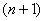
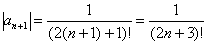
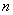
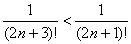
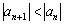
Ряд сходится по признаку Лейбница.

Исследуем характер сходимости: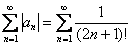

Используем признак Даламбера: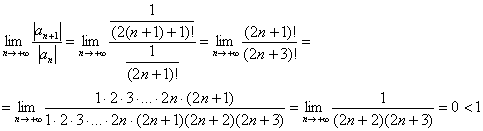

Таким образом, ряд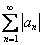 сходится.
Ряд 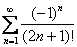сходится абсолютно.

Примечание: Возможно, не всем понятно, как разложены факториалы. Это всегда можно установить опытным путём, возьмём и сравним какие-нибудь соседние члены ряда:
и , следующий член ряда к предыдущему:
и , следующий член ряда к предыдущему:
…

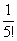
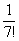
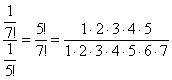
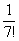
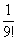
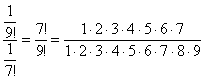
Таким образом, ряд сходится. Выясним, абсолютно или условно: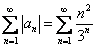

Используем признак Даламбера: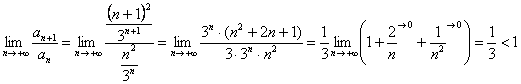
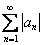
, следовательно , ряд сходится.
Исследуемый ряд сходится абсолютно.

Пример 10: Используем признак Лейбница.
1)
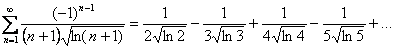
Ряд является знакочередующимся.
2) – члены ряда убывают по модулю, и очевидно, что – каждый следующий член ряда по модулю меньше предыдущего: , т.е. убывание монотонно.

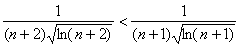
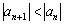
Ряд сходится по признаку Лейбница.

Исследуем ряд, составленный из модулей: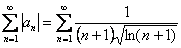

Используем интегральный признак.

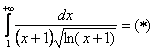
Подынтегральная функция непрерывна на .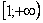

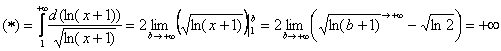
Таким образом, ряд 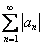расходится вместе с соответствующим несобственным интегралом.

Исследуемый ряд сходится условно.

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

Источник