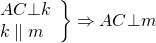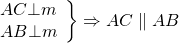Докажите что серединные перпендикуляры к двум сторонам треугольника пересекаются
Серединные перпендикуляры к сторонам треугольника
Свойство серединных перпендикуляров к сторонам треугольника
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
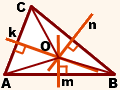
m, n, k — серединные перпендикуляры к сторонам AB, BC, AC
Доказать: m, n, k пересекаются в одной точке.
Сначала докажем, что серединные перпендикуляры к двум сторонам треугольника пересекаются в одной точке.
Предположим, что m и k не пересекаются. Тогда m ∥ k.
Но прямые AB и AC пересекаются в точке A. Пришли к противоречию. Следовательно, прямые m и k пересекаются.
Обозначим точку пересечения прямых m и k как O.
По свойству серединного перпендикуляра к отрезку AO=OC и AO=BO. Следовательно, и OC=BO. Значит, точка O равноудалена от концов отрезка BC, следовательно, лежит на серединном перпендикуляре n к этому отрезку. Таким образом, все три серединных перпендикуляра m, n, k к сторонам треугольника ABC пересекаются в одной точке O.
Что и требовалось доказать.
Точка пересечения серединных перпендикуляров к сторонам треугольника является центром описанной около этого треугольника окружности
Точка пересечения серединных перпендикуляров к сторонам треугольника — одна из четырех замечательных точек треугольника.
Докажите что серединные перпендикуляры к двум сторонам треугольника пересекаются?
Это может доказать любой человек, даже не будучи большим знатоком в геометрии. Ведь перпендикулярно пересекающиеся линии всегда дают угол 90% в точке соединения или пересечения (это все знают). Сумма двух внутренних углов, от двух проведённых серединных перпендикуляров к двум любым сторонам любого треугольника (будь то равнобедренный, равносторонний или неправильный треугольник) всегда будет равна 180% (90% + 90% = 180%). А угол в точке соединения двух любых сторон треугольника, т.е. внутренний угол между этими сторонами, а, соответственно, и между перпендикулярами, проведёнными к ним, всегда будет меньше 180%, т. к. только развёрнутый угол (или попросту прямая) имеет значение 180%. Но ведь мы все знаем, что не существует таких треугольников, которые имели бы хотя бы один развёрнутый угол. Внутренние углы треугольника могут быть как тупыми, так и острыми, но никогда развёрнутыми! А теперь судите сами, если внутренний угол между двумя сторонами треугольника имеет значение даже 179% ( что меньше значения развёрнутого угла всего на 1%), то получается, что перпендикуляры, проведённые к этим сторонам, не являются параллельными прямыми. А не параллельные линии всегда пересекаются. Раньше или позже, но всё-равно всегда пересекаются. Это тоже все знают.
Вы можете войти или зарегистрироваться, чтобы добавить ответ и получить бонус.