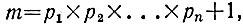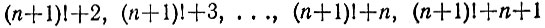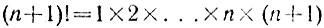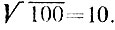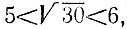Докажите что следующие числа являются составными

Докажите что следующие числа являются составными

Составные числа

Число так называемых простых чисел, т. е. целых чисел, больших единицы, не делящихся без остатка ни на какие другие целые числа, кроме единицы и самих себя, бесконечно велико.

Для удобства будем пользоваться условным символом n!, который обозначает произведение всех чисел от 1 до n включительно. Например 5! = 1 × 2 × 3 × 4 × 5. Мы сейчас докажем, что ряд

включительно состоит из n последовательных составных чисел.

состоит из двух слагаемых, каждое из которых кратно 3. Значит, и это число составное.

делится без остатка на 4, так как состоит из слагаемых, кратных 4.

Подобным же образом устанавливаем, что следующее число

кратно 5 и т. д. Иначе говоря, каждое число нашего ряда содержит множитель, отличный от единицы и его самого; оно является, следовательно, составным.

Если вы желаете написать, например, пять последовательных составных чисел, вам достаточно в приведенный выше ряд подставить вместо n число 5. Вы получите ряд

Или еще меньшие числа:

Попробуем теперь решить задачу:

Написать десять последовательных составных чисел.

На основании ранее сказанного устанавливаем, что в качестве первого из искомых десяти чисел можно взять

Искомой серией чисел, следовательно, может служить такая!

Однако существуют серии из десяти гораздо меньших последовательных составных чисел. Так, можно указать на серию даже не из десяти, а из тринадцати составных последовательных чисел уже во второй сотне:

Источник

math4school.ru

Простые и составные числа

Немного теории

Простое число – это натуральное число, имеющее ровно два различных натуральных делителя: единицу и само себя. Все остальные натуральные числа, кроме единицы, называются составными. Таким образом, все натуральные числа больше единицы разбиваются на простые и составные. Изучением свойств простых чисел занимается теория чисел.

Приведём некоторые свойства простых чисел.

Основная теорема арифметики. Каждое натуральное число, большее единицы, представимо в виде произведения простых чисел, причём единственным способом с точностью до порядка следования сомножителей.

Простых чисел бесконечно много.

Если p – простое, и p делит a·b, то p делит a или b.

Mалая теорема Ферма. Если p – простое, a – натуральное, то a p – a делится на p.

Теорема Вильсона. Натуральное p > 1 является простым тогда и только тогда, когда (p – 1)! + 1 делится на p.

Постулат Бертрана. Если n > 1 – натуральное, то существует простое p, такое, что n 1 – целые взаимно простые числа, содержит бесконечно много простых чисел.

Теорема Ферма. Каждое простое число вида 4k + 1 есть сумма двух квадратов натуральных чисел.

Всякое простое число, большее 3, представимо в виде 6k + 1 или 6k – 1, где k – некоторое натуральное число.

Число, следующее за простым, не может быть квадратом или более высокой степенью с основанием, большим 2.

Число, предшествующее простому, не может быть кубом или более высокой нечётной степенью с основанием, большим 1.

Задачи с решениями

1. Три простых числа, каждое из которых больше 10, образуют арифметическую прогрессию. Докажите, что разность прогрессии делится на 6.

Все данные простые числа нечётные, поэтому их разность делится на 2. Покажем, что она делится и на 3. Пусть данные числа a, a + d, a + 2d. Ни одно из них не делится на 3, поэтому при делении на 3 даёт остаток или 1, или 2. Следовательно, по крайней мере, два из этих чисел дают при делении на 3 одинаковые остатки. Разность этих чисел, равная d или 2d, делится на 3. Поскольку 2 на 3 не делится, то d делится на 3. Итак, разность прогрессии, которая делится на взаимно простые числа 2 и 3, делится на 6, что и требовалось доказать.

2. Докажите, что для произвольного натурального числа n найдётся натуральное m такое, что nm + 1 – составное число.

Можно выбрать m = n + 2, тогда

nm + 1 = n(n + 2) + 1 = n 2 + 2n + 1 = (n + 1) 2

является составным числом.

3. Найдите все целые числа n, для которых модуль значения трёхчлена n 2 – 7n + 10 будет простым числом.

|n 2 – 7n + 10| = |n –2| · |n – 5|,

то следует искать такие n при которых один из множителей последнего произведения равен 1, а второй является простым числом. Этому требованию удовлетворяют n = 3 и n = 4.

4. Докажите, что если числа

а) m и m 2 + 2 простые, то число m 3 + 2 тоже простое;

б) р, р – 10, р + 10 простые, то число р – 2 тоже простое.

а) Любое простое число m, отличное от 3, можно представить в виде 3n+1 или в виде 3n–1, где n – некоторое натуральное число. В первом случае можно записать

m 2 + 2 = 9n 2 + 6n +3,

m 2 + 2 = 9n 2 – 6n +3,

Так как m > 2, то в любом случае число m 2 +2 больше 3 и делится на 3, а значит является составным. Следовательно, число m 2 +2 может быть простым, только если m = 3. В этом случае m 2 +2 = 11 – простое число, m 3 +2 = 29 – тоже простое число, что и требовалось доказать.

б) Так как р – 10 = (р – 1) – 9 и р + 10 = (р + 1) + 9, то числа р – 10 и р – 1 при делении на 3 имеют одинаковые остатки, и числа р + 10 и р + 1 при делении на 3 имеют одинаковые остатки.

Из трёх последовательных чисел р – 1, р, р + 1 одно и только одно делится на 3. С учётом выше сказанного, то же утверждение верно для чисел р – 10, р, р + 10. Так как эти числа простые, то р – 10 = 3 и р = 13, поэтому р – 2 = 11 – простое число, что и требовалось доказать.

5. Сколько раз входит двойка в разложение на простые множители произведения

Ответ на поставленный вопрос получим из следующих преобразований:

6. Найдите все простые p такие, что число p 2 + 11 имеет ровно 6 различных делителей (включая единицу и само число).

Если p > 5 и простое, то числа p – 1 и p + 1 оба четные, и одно из них кратно трем. Поэтому произведение (p – 1)(p + 1) делится на 12, следовательно, p 2 + 11 также делится на 12, а значит, имеет не менее семи делителей (6 делителей числа 12 и само число p 2 + 11 > 12 ). Осталось проверить p = 2 и p = 3.

Если p = 2, то p 2 + 11 = 2 2 + 11 = 15 имеет 4 делителя (1, 3, 5, 15).

Если p = 3, то p 2 + 11 = 3 2 + 11 = 20 имеет 6 делителей (1, 2, 4, 5, 10, 20).

7. Найти все натуральные числа n, для которых каждое из шести чисел

n + 1, n + 3, n + 7, n + 9, n + 13 и n + 15

Рассмотрим варианты. Для n = 1 число n + 3 = 4 составное.

Для n = 2 число n + 7 = 9 составное.

Для n = 3 число n + 1 = 4 составное.

Для n > 4 все наши числа больше 5 и по крайней мере одно из них делится на 5, так как числа 1, 3, 7, 9, 13 и 15 при делении на 5 дают соответственно остатки 1, 3, 2, 4, 3 и 0, то есть все возможные остатки, откуда следует, что и числа

n + 1, n + 3, n + 7, n + 9, n + 13 и n + 15

при делении на 5 дают все возможные остатки и, следовательно, хотя бы одно из них делится на 5 и как число, большее пяти (так как n > 4), является составным.

Но для n = 4 мы получаем простые числа 5, 7, 11, 13, 17 и 19.

8. Доказать, что каждое простое число вида 4k + 1 является длиной гипотенузы прямоугольного треугольника, стороны которого выражаются натуральными числами.

9. Сколькими способами можно раскрасить круг, разбитый на р равных секторов с помощью n красок, если р – простое число и каждый сектор раскрашиваем одной краской? Две раскраски, совпадающие при повороте круга, считаем одинаковыми.

Каждый сектор можно раскрасить в любой из n цветов, поэтому для круга с р секторами получим n p раскрасок, среди которых (n p – n) не одноцветных. Каждая из этих раскрасок поворотами переходит в (р – 1) одинаковую с ней, значит, существенно различных не одноцветных раскрасок будет (n p – n)/p, откуда общее число раскрасок равно n + (n p – n)/p.

10. Доказать, что для любого простого числа p > 5 уравнение х 4 + 4 x = p в целых числах не имеет решений.

Докажем, что если для некоторого целого значения х число

является целым, то это число либо не превосходит пяти, либо является составным.

Действительно, если х 4 + 4 0 4 + 4 1 = 5.

Если x = 2k (k – натуральное число), то число

f(x) = 2 4 k 4 + 4 2k = 2 4 ( k 4 + 4 2(k–1) )

Наконец, если x = 2k + 1 (k – натуральное число), то число

f(x) = x 4 + 4·4 2k = (x 4 + 4x 2 (2 k ) 2 + 4(2 k ) 4 ) – 4x 2 (2 k ) 2 =

= (x 2 + 2(2 k ) 2 ) 2 – (2·x·2 k ) 2 =

= (x 2 + 2·x·2 k + 2(2 k ) 2 )·( x 2 – 2·x·2 k + 2(2 k ) 2 ) =

= ((x + 2 k ) 2 + 2 2k )·((x – 2 k ) 2 + 2 2k )

так же является составным, поскольку каждый из двух сомножителей последнего произведения больше 1 (ибо 2 2k > 1 при k > 0).

Таким образом, если число p > 5 простое, то равенство х 4 + 4 x = p не выполняется ни при каких целых значениях х.

Задачи без решений

1. Известно, что р, р + 10, р + 14 – простые числа. Найдите число р.

2. Докажите, что число

3. Найдите все простые р для которых число р 2 + 14 так же будет простым числом.

4. Докажите, что уравнение х 2 + х + 1 = р·у имеет решение в целых числах (х, у) для бесконечного числа простых р.

5. Введём обозначение для суммы первых n простых чисел через S_n:

Докажите, что между числами S_n и S_n+1 всегда существует число, являющееся полным квадратом.

Источник

Простые и составные числа, определения, примеры, таблица простых чисел, решето Эратосфена

В статье рассматриваются понятия простых и составных чисел. Даются определения таких чисел с примерами. Приводим доказательство того, что количество простых чисел неограниченно и произведем запись в таблицу простых чисел при помощи метода Эратосфена. Будут приведены доказательства того, является ли число простым или составным.

Простые и составные числа – определения и примеры

Простые и составные числа относят к целым положительным. Они обязательно должны быть больше единицы. Делители также подразделяют на простые и составные. Чтобы понимать понятие составных чисел, необходимо предварительно изучить понятия делителей и кратных.

Составными числами называют целые числа, которые больше единицы и имеют хотя бы три положительных делителя.

Единица не является ни простым ни составным числом. Она имеет только один положительный делитель, поэтому отличается от всех других положительных чисел. Все целые положительные числа называют натуральными, то есть используемые при счете.

Простые числа – это натуральные числа, имеющие только два положительных делителя.

Составное число – это натуральное число, имеющее более двух положительных делителей.

Натуральные числа, которые не являются простыми, называют составными.

Таблица простых чисел

Для того, чтобы было проще использовать простые числа, необходимо использовать таблицу:

Рассмотрим теорему, которая объясняет последнее утверждение.

Наименьший положительный и отличный от 1 делитель натурального числа, большего единицы, является простым числом.

Простых чисел бесконечно много.

Видно, что может быть найдено любое простое число среди любого количества заданных простых чисел. Отсюда следует, что простых чисел бесконечно много.

Решето Эратосфена

Данный способ неудобный и долгий. Таблицу составить можно, но придется потратить большое количество времени. Необходимо использовать признаки делимости, которые ускорят процесс нахождения делителей.

Перейдем к формулировке теоремы.

Данное число простое или составное?

Перед решением необходимо выяснять, является ли число простым или составным. Зачастую используются признаки делимости. Рассмотрим это на ниже приведенных примере.

Доказать что число 898989898989898989 является составным.

Ответ: 11723 является составным числом.

Источник

№ 636. ГДЗ Математика 5 класс Никольский. Помогите доказать, что число является составным.

Используя признаки делимости, докажите, что число:
а) 7690; 6)7395; в) 4256; г) 12 375; д) 12 321
является составным.

а) 7690 = 2 ∙ 3845 — составное
б) 7395 = 5 ∙ 1479 — составное
в) 4256 = 2 ∙2128 — составное
г) 12375 = 2475 ∙ 5 — составное
д) 12321 =3 ∙4107 — составное

Вычислите объём прямоугольного параллелепипеда, если его рёбра равны:
а) 18 см, 16 см, 5 см; б) 12 см, 45 см, 2 ( Подробнее. )

Самолёт поднялся в воздух в 14 ч 45 мин и приземлился в 17 ч 10 мин. Сколько времени он находился в полёте?

1. Через середину М сторони АВ трикутника АВС проведено площину, яка паралельна, прямій АС і перетинає сторону ВС у точці N. Довести NM ( Подробнее. )

Привет…Не могу справиться с ответом на такой вопрос…может кто поможет, а?
Чтобы пройти в следующий круг соревнований, футбольной ( Подробнее. )

Привет пользователи! Окажите пожалуйста услугу…ответить помогите….
В Волшебной стране бывает два типа погоды: хорошая и отличная, ( Подробнее. )

Источник

§ 4. Простое или составное?

При решении многих практических задач, в которых участвуют натуральные числа, немаловажную роль играет разложение этих чисел на множители, Основными «кирпичиками» в таком разложении являются простые числа, т. е. числа, большие 1 и делящиеся только на 1 и на себя. Остальные натуральные числа, большие 1, называются составными (число 1 не относится ни к простым, ни к составным). Основная теорема арифметики гласит, что всякое натуральное число, кроме 1, может быть представлено в виде произведения простых множителей, причем это представление единственно, если отвлечься от порядка множителей.

Издавна математиков интересовали вопросы о количестве и других свойствах простых чисел, а также о возможностях разложения конкретных чисел на простые множители. Еще Евклидом было доказано, что простых чисел бесконечно много. Древнегреческому математику Эратосфену был известен удобный способ отыскания простых чисел, который был назван решетом Эратосфена. Благодаря титаническим усилиям ряда ученых удалось получить ответы на многие, но пока не на все вопросы, связанные с распределением простых чисел в натуральном ряду. Что же касается разложения чисел на простые множители, то эта задача для больших чисел остается довольно трудной и по сей день.

Докажите, что составных чисел бесконечно много,

Докажите, что простых чисел бесконечно много.

Могут ли два простых числа оказаться идущими подряд? А три?

Найдите пять последовательных натуральных чисел, каждое из которых является составным. Для любого ли натурального значения n можно подобрать n таких чисел?

Чтобы узнать, является ли данное натуральное число n составным, достаточно проверить, имеет ли оно хотя бы один делитель, больший 1 и меньший n. Докажите, что эту работу можно сократить, ограничившись проверкой делимости числа n только на простые числа и к тому же не превосходящие

Разложить на простые множители число: а) 315; б) 127; в) 1001; г) 899; д) 919.

Выпишем подряд все натуральные числа от 1 до некоторого числа п и зачеркнем число 1. Возьмем первое незачеркнутое число, большее 1,- это будет число 2,- и зачеркнем каждое второе число, начиная отсчет от числа 2+1. Затем возьмем первое незачеркнутое число, большее 2,- это будет число 3,- и зачеркнем каждое третье число, начиная отсчет от числа 3 + 1 (ранее зачеркнутые числа также отсчитываются). Затем возьмем первое незачеркнутое число, большее 3,- это будет число 5,- и зачеркнем каждое пятое число, начиная отсчет от числа 5 + 1. Продолжая действовать так и далее, остановимся тогда, когда первое незачеркнутое число, большее предыдущего, окажется большим 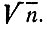Докажите, что в итоге незачеркнутыми останутся все простые числа, не превосходящие n, и только они.

Используя решето Эратосфена, выпишите все простые числа, не превосходящие 100.

Выпишите все простые числа, находящиеся между числами 120 и 150.

Описанную в задаче 4.7 процедуру отыскания простых чисел можно упростить, если с самого начала не выписывать чисел, кратных 2, 3 или 5: Найдите все остатки от деления на 30, которые могут давать числа, не делящиеся ни на 2, ни на 3, ни на 5.

Выпишите все простые числа, находящиеся между числами 470 и 520.

Решения

4.1. Все четные числа, большие 2 (а их бесконечно много), являются составными, так как каждое из них делится на 1, на себя и на 2.

4.3. Если два простых числа идут подряд, то одно из них четно, а значит, равно 2 (см. решение задачи 4.1). Тогда второе число непременно равно 3, поскольку 1 не является простым числом. Итак, нами найдена единственная пара идущих подряд простых чисел. Отсюда следует, что тройки идущих подряд простых чисел не существует, так как из такой тройки можно было бы образовать две различные пары идущих подряд простых чисел, а именно первое число со вторым и второе с третьим.

4.4. Последовательные числа 24, 25, 26, 27, 28 образуют искомую пятерку. Докажем, что для любого натурального значения n найдутся n идущих подряд составных чисел. В самом деле, каждое из n чисел

является составным, поскольку число

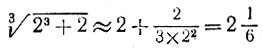
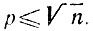
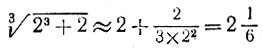
4.5. Докажем, что любое составное число n имеет простой делитель, не превосходящий Возьмем наименьшее простое число р, участвующее в разложении числа n на простые множители. Тогда число n представляется в виде произведения pq, причем p≤q, поэтому p 2 ≤pq = n и Из доказанного утверждения следует, что если число n не делится ни на одно простое число, не превосходящее , то оно является простым.

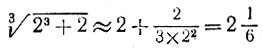
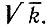
4.7. В результате описанной в условии задачи процедуры в ряду чисел от 1 до л не будет зачеркнуто ни одно простое число, так как на каждом шагу зачеркиваются только числа, кратные каким-то другим числам. Число k (большее 1) из этого ряда останется незачеркнутым только в том случае, если оно не делится ни на одно из незачеркнутых чисел, не превосходящих , среди которых содержатся все простые числа, не превосходящие Согласно задаче 4.5, таким числом к может быть только простое число. Таким образом, в ряду останутся незачеркнутыми все простые числа и только они.

4.8. Зачеркнув в ряду чисел от 1 до 100 сначала число 1, затем числа, кратные 2, кроме числа 2, затем числа, кратные 3, кроме числа 3, затем числа, кратные 5, кроме числа 5, и, наконец, числа, кратные 7, кроме числа 7, мы получим следующий набор незачеркнутых чисел:

На этом следует остановиться, поскольку следующее за числом 7 незачеркнутое число 11 уже превосходит

4.9. Так как 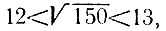то наименьший простой делитель любого из составных чисел, меньших 150, не превосходит 11 (см. задачу 4.5). Вычеркнем из ряда чисел от 120 до 150 все числа, делящиеся на 2, 3 или 5, тогда останутся числа

4.10. Число не делится ни на 2, ни на 3, ни на 5 в том и только в том случае, если его остаток от деления на 30=2x3x5 не делится ни на одно из этих чисел. Так как

то, вычеркнув из всех возможных значений остатков от деления на 30, т. е. из чисел от 0 до 29, числа, кратные 2, 3 или 5, мы получим число 1 и все простые числа (см. задачу 4.7). Следовательно, набор искомых остатков выглядит так:

Благодаря этому наблюдению при отыскании простых чисел (больших 5) можно выписывать не все числа подряд, а только те, которые дают указанные здесь восемь остатков от деления на 30, что позволяет сэкономить работу по выписыванию в 30 /₈ = 3,75 раза. Именно так можно было поступить, например, при решении задачи 4.9.

4.11. Так как 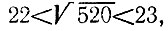то наименьший простой делитель любого из составных чисел, меньших 520, не превосходит 19 (см. задачу 4.5). Согласно результату задачи 4.10, простые числа могут оказаться лишь среди 12 чисел

Из этих чисел теперь остается только вычеркнуть числа, кратные 7 (497, 511), кратные 11 (473, 517), кратные 13(503), кратные 17 (493) и кратные 19 (таких нет), и получить окончательный набор

Источник