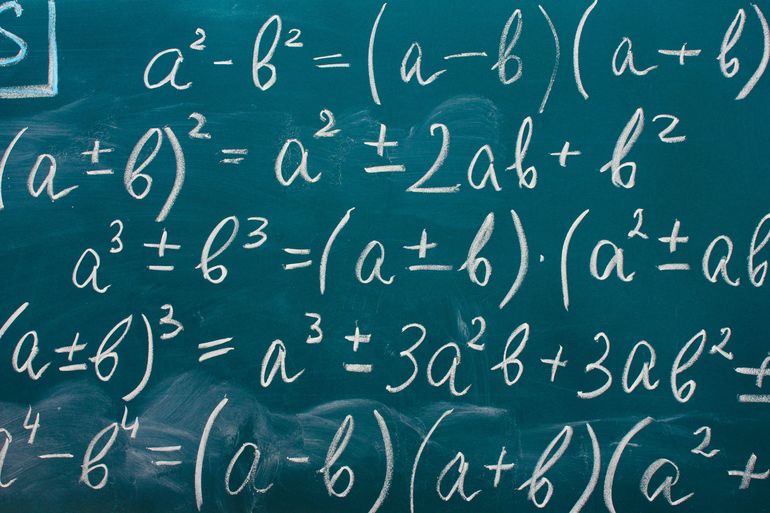Докажите что сумма кубов является точным квадратом
Метод математической индукции
п.1. Принцип математической индукции
Говорят, что мы провели « доказательство утверждения Pn индукцией по n ».
Принцип математической индукции используется для доказательства различных формул.
Например:
Докажем, что сумма первых n натуральных чисел равна \(\mathrm
1) Для базы индукции \(\mathrm
2) Допустим что при некотором \(\mathrm
Что и требовалось доказать.
п.2. Примеры
Пример 1. Докажите, что сума кубов первых n натуральных чисел равна \(\mathrm
1) Для базы индукции \(\mathrm
2) Допустим, что при некотором \(\mathrm
Пример 3. Докажите, что любой член последовательности an = 15 n + 6 делится на 7.
1) Для базы индукции n=1, a1 = 15 + 6 = 21 – делится на 7, верно
2) Допустим, что при некотором \(\mathrm
Следовательно, по принципу математической индукции an = 15 n + 6 делится на 7 при любом натуральном \(\mathrm
Возвращаемся к основной задаче: \(\mathrm<\frac
Значит, an+1 делится на 18 с остатком 1. Индуктивный переход для основной задачи выполняется.
Следовательно, по принципу математической индукции an = 7 n + 12n делится на 18 с остатком 1 при любом натуральном \(\mathrm
Точные квадраты и кубы
Точно так же у точного куба число делителей имеет вид 3n+1, у четвертой степени — число вида 4n+11 и т.д.
При работе со степенями целых и натуральных чисел всегда следует иметь в виду, что степень с большим показателем также является и степенью с маленьким показателем: например, а 100 — это одновременно и квадрат пятидесятой степени, и четвертая степень двадцать пятой степени, и пятая степень двадцатой степени, и т.п. Ясно, что показатель степени таким образом можно уменьшить для любого составного числа n, а для простого n это ничего не даст.
При решении задач полезным может оказаться следующее свойство точных квадратов:
Квадрат числа при делении на любое число дает тот же остаток, что и квадрат его остатка.
Например, число k при делении на 6 может давать остатки 0, 1, 2, 3, 4, 5, их квадраты — 0, 1, 4, 9, 16, 25, а остатки от деления квадратов на 6 — это 0, 1, 4, 3, 4, 1. Таким образом, квадрат числа при делении на 6 не может давать остатков 2 и 5.
Теми же рассуждениями легко получить, что возможные остатки при делении точного квадрата на 3 и на 4 — это 0 или 1.
Ответ: Все три числа в заданной сумме нечетны, следовательно, их квадраты имеют вид 4п+1, так что их сумма имеет вид 4т+3 и поэтому не является точным квадратом.
Пример 3: Доказать, что если два числа оба не делятся на 3, то их сумма не является точным квадратом.
Ответ: Так как квадрат любого натурального числа, не делящегося на 3, при делении на 3 дает остаток 1, то сумма любых двух таких чисел при делении на 3 дает остаток 2, а такое число не может быть точным квадратом.
Краткое описание
В алгебре большим спросом пользуются различные формулы и соответствующие правила сокращённого умножения. При правильном подходе ученик может максимально быстро и правильно решать большие уравнения. Универсальные формулы были получены специалистами для умножения и вычитания сразу нескольких многочленов. Только подготовленные ученики могут максимально быстро решать поставленные задачи, существенно упростив используемое выражение. Базовые правила востребованных преобразований позволяют выполнять определённые манипуляции с уравнениями.
Если максимально придерживаться основных рекомендаций, то можно будет получить в левой части примера равенство выражения, расположенное с правой стороны. Ученик должен хорошо владеть теми формулами, которые применяются для сокращённого умножения, используемого во время решения задач, а также уравнений. Но даже в этом случае нужно соблюдать ряд нюансов, чтобы можно было избежать допущения грубых ошибок.
Интересным фактом является то, что некоторые формулы для быстрого умножения были выведены экспертами ещё в конце четвёртого тысячелетия до нашей эры. Именно целеустремлённые греки максимально развили идеи своих предшественников, из-за чего им удалось разработать сразу несколько важных и полезных правил. Но в те времена математики мыслили совершенно иначе, так как они стремились воссоздать числа с помощью подручных материалов или геометрических фигур. К примеру: специально обтёсанные камни на счётной доске из дерева.
Ещё несколько лет назад формулы для определения суммы различных величин выводились исключительно геометрическим методом. Эксперты практиковали рассечение квадрата на разные фрагменты. Настоящий подъём науки пришёлся на времена Ньютона и других учёных. Именно эти целеустремлённые люди смогли внести огромный вклад в развитие формул для алгебры, представив обществу усовершенствованный вариант.
Сумма и разность кубов
Для изучения этой темы должно быть отведено достаточно времени, так как только после изучения всех нюансов ученик сможет должным образом применить свои знания. Основная формула суммы кубов двух чисел выглядит следующим способом: w3 + y3 = (w + y) (w2 — wy + y2). Стоит отметить, что задействованное выражение w2 — wy + y2 отличается от правой части только присутствующим коэффициентом при y. Именно поэтому такое выражение называют неполным квадратом разности.
Обязательно нужно усвоить правило, что итог двух кубических (ударение падает на слог с первой буквой «и») корней будет соответствовать произведению суммы этих выражений на неполный квадрат их разности. Нужно понимать, что каждая математическая задача обладает определёнными характеристиками, которые нельзя оставить без внимания.
Элементарную формулу сумму кубов получают следующим образом:
Зафиксированная сумма кубов раскладывается по специальной технологии, так как разность кубов двух уравнений равна произведению разности этих уравнений на неполный квадрат их суммы. В качестве примера можно изучить следующую задачу:
По описанному примеру можно понять, что решать поставленные задачи можно быстро и без ошибок, но это только в том случае, если заранее изучить все правила. Ученику необходимо решить минимум три задачи, чтобы увидеть разницу между уравнениями и выполнить полное раскрытие темы.
Основное доказательство ФСУ
Во время изучения математики перед учениками неизбежно возникает необходимость определить сумму кубов. Примеры решения элементарных и более сложных задач позволяют лучше усвоить тему. Основное доказательство ФСУ отличается своей простотой и элементарностью. Базируясь на свойствах умножения можно правильно выполнять сложение цифр из всех частей формул в скобках. В качестве примера можно рассмотреть формулу квадрата разности: d — r2= d−2dr + r2.
Чтобы иметь возможность возвести пример во вторую степень, необходимо задействованное выражение умножать само на себя:
После этого можно считать, что формула полностью доказана. Все остальные ФСУ описываются подобным образом.
Основная цель применения математических приёмов — максимально быстрое и правильное умножение, а также возведение в степень имеющихся выражений. Но это далеко не все способы использования ФСУ. Распространённые методы сокращённого умножения применяются для упрощения выражений, разложение задействованных многочленов на множители, а также для работы с различными дробями.
При правильном подходе ФСУ позволяет даже вычислить значения математических выражений. Главная задача — иметь достаточно навыков, чтобы заметить, где именно будет уместна формула. Если по условиям задачи нужно возвести в квадрат любое число (к примеру: 79), тогда вместо громоздких вычислений можно прибегнуть к более лаконичным и понятным записям: 79=80−1; 792=80−12=6400−160+1=6241.
Формулы умножения с упрощённой схемой и специальные таблицы позволяют гораздо быстрее выполнить все необходимые вычисления. Определённые сложности могут возникнуть с выделением квадрата двучлена, так как в этом случае можно допустить много ошибок.
Математическое выражение 4х2+4х-3 можно легко преобразовать. В этом случае можно получить следующий результат: 2х2 +2*2*х *1 +12−4=2х+12−4. Интересным является то, что именно такое преобразование активно используется в интегрировании.
Вспомогательная информация
Именно сумма сразу двух геометрических кубов получила большой спрос в алгебре для кардинального упрощения многочленов. Лучше всего рассматривать конкретные примеры, которые относятся к категории сложных уравнений. Без наставлений учителя решать такие задачи при помощи универсального тригонометрического аппарата будет крайне сложно, особенно для неподготовленного школьника.
Грубые ошибки допускают те, кто плохо знаком со свойствами синусов и косинусов. На помощь может прийти правило суммы двух кубов, так как все описанные примеры максимально повторяют разложение на отдельные множители выражения a 2 + b 2. Но в этом случае вместо а — sinx, а b заменил cosy.
Если следовать правилам, то многоуровневое тригонометрическое выражение может легко превратиться в лаконичную запись, где sin3x + cos3y. После этого остаётся применить эту универсальную формулу во время подсчёта. Многие люди практически на память знают все квадраты к используемым в повседневной жизни натуральным числам до пятнадцати. А ученики, которые занимаются арифметикой на постоянной основе, владеют большим количеством квадратов. Гораздо сложнее работать с кубами. Если по условиям задачи нужно посчитать сумму двух таких кубов, то гораздо практичнее и быстрее применить формулу разложения на отдельные множители.
На просторах интернета много различных программ, которые считают сумму двух кубов с различными иллюстрациями промежуточных вкладов. Эта разработка программистов пригодится школьникам, стремящимися проверить результаты выполненных работ, а также взрослым, которые хотят возобновить в памяти школьный курс алгебры.
Особенности использования уравнений
Для лучшего усвоения этой темы следует более подробно изучать приведённые примеры. В качестве основы следует взять элементарную формулу для квадрата суммы двух чисел: h+ hl = h2+2 hl + l2. Этот математический пример необходимо читать только таким образом: квадрат суммы для двух выражений h и l соответствует квадрату первого выражения, удвоенного произведения уравнения, а также квадрату второго выражения. Точно таким образом математики читаются все остальные формулы.
Если нужно записать квадрат разности h — l2= h2−2hl + l2. Запись такого уравнения выглядит только так: квадрат математической разности двух примеров максимально соответствует конечной сумме, которая была получена от квадрата этих утверждений. Но также перед учеником может возникнуть необходимость правильно прочитать более сложную формулу: h + l3= h3+3h2l +3hl 2+ l3. Задействованный куб суммы двух математических уравнений соответствует итоговым данным этого примера. В этом уравнении присутствует утроенное произведение квадрата первого выражения на второе.
Ключевые нюансы
Если есть необходимость самостоятельно вычислить куб суммы двух слагаемых, тогда первым делом определяют сумму, которая включает в себя куб первого слагаемого, утроенного произведения квадрата первого и второго слагаемого. В алгебре это выражение выглядит так: (d+e) 3 = d 3 +3 d 2 e +3 de 2 + e 3.
Специальные формулы сокращённого умножения являются неотъемлемой темой в школьной программе по алгебре, так как она обязательно пригодится во время решения многоуровневых задач. Это своеобразная основа, на которой строятся решения интегральных исчислений. Онлайн-калькуляторы помогают лучше освоить технологию применения формулы двух кубов, которые можно свернуть, а потом снова открыть для приведения уравнения в нужный вид.
Почему сумма трёх кубов – это такая сложная математическая задача
Тяжело искать ответы в бесконечном пространстве. Математика уровня старших классов может помочь вам сузить область поисков.
Учитывая, что люди изучают свойства чисел тысячи лет, можно было бы решить, что нам известно всё о числе 3. Однако недавно математики обнаружили нечто новое касательно числа 3: третий способ выразить это число в виде суммы трёх кубов. Задача записи числа через сумму трёх кубов целых чисел оказывается неожиданно интересной. Легко показать, что большую часть чисел нельзя записать в виде одного куба или суммы из двух кубов, но существует гипотеза, что большую часть чисел можно записать в виде суммы из трёх кубов. Однако найти эти кубы оказывается иногда чрезвычайно сложно.
Если вам захочется проверить этот результат, не пытайтесь использовать калькулятор. Большинство из них не справится с таким количеством цифр. Но с этим справится WolframAlpha.
В поисках новых вариантов решений для числа 3, математики используют техники, придуманные в этом году Буккером, первым нашедшим сумму трёх кубов для числа 33. Но почему на подобные прорывы требуется столько времени? В поисках правильных кубов приходится покрывать очень большую территорию, а нужное направление нам может указать лишь небольшое число подсказок. Поэтому фокус состоит в том, чтобы найти более хитрые методы поиска. Чтобы представить себе саму задачу и её решение, начнём с более простого вопроса: как мы можем записать 33 в виде суммы трёх целых чисел?
Мы можем записать 33 = 19 + 6 + 8, или 33 = 11 + 11 + 11, или 33 = 31 + 1 + 1. Мы можем использовать и отрицательные числа: 33 = 35 + (−1) + (−1). Существует бесконечное множество способов сделать это, поскольку всегда можно увеличить одно или два числа и уменьшить третье для компенсации этого – например, 33 = 36 + (−1) + (−2), 33 = 100 + 41 + (−108), и так далее.
При суммировании квадратов у нас нет той же гибкости, что при суммировании любых целых чисел. У нас меньше выбор, и, что ещё важнее, сложение лишь увеличивает нашу сумму. Ведь квадраты целых чисел не бывают отрицательными – возведение в квадрат и положительного и отрицательного числа всегда даёт положительное.
Имея шесть вариантов для каждого их трёх квадратов, мы получаем не более 6 × 6 × 6 = 216 способов записать 33 как их сумму. Достаточно небольшой список для того, чтобы проверить все возможности и убедиться, что мы ничего не пропустили.
Неограниченность пространства поиска означает, что мы можем искать ответы очень долго. И люди искали их десятилетиями. Понадобился суперкомпьютер и хитрая математика, чтобы найти, наконец, правильную комбинацию кубов. Давайте посмотрим, как это удалось сделать.
Допустим, вам нужно найти решение уравнения:
Простой подход – разметить некий регион чисел и подставлять каждый из них, пока что-нибудь не подойдёт. Если вы ничего не найдёте, можно определить новое пространство поиска и начать сначала. Это похоже на поиск новых планет при помощи методичного изучения неба в телескоп.
(−100) 3 + (−100) 3 + (−100) 3
Не вышло. Тогда вы пробуете:
(−99) 3 + (−100) 3 + (−100) 3
Тоже не работает. Вы продолжаете, пока не дойдёте до (100, −100, −100), потом переключаетесь на (−100, −99, −100), и вновь продолжаете свою охоту. В итоге вы проверите порядка 200 × 200 × 200 = 8 000 000 вариантов, не найдя ничего подходящего. Придётся обозначить новое пространство поиска и начать заново.
Более интересный подход – переписать уравнение в следующем виде:
33 – (x 3 + y 3 ) = z 3
Ещё более удобный подход — переписать уравнение в следующем виде:
Теперь мы перебираем z, а для каждого вычисленного z мы используем хитрый фокус из курса математики. Выражение x 3 + y 3 всегда можно разложить так:
x 3 + y 3 = (x + y)(x 2 – xy + y 2 )
Это формула для суммы кубов. Чтобы проверить её, просто перемножим правую часть, пользуясь правилом дистрибутивности:
(x + y)(x 2 – xy + y 2 ) = x 3 – x 2 y + xy 2 + yx 2 – xy 2 + y 3 = x 3 + y 3
Такой метод позволяет вместо 200 3 = 8 000 000 троек или даже 200 2 = 40 000 пар исследовать 200 возможных вариантов z. Дополнительную работу составляют разложение на множители и проверка, но в целом поисковая эффективность серьёзно растёт. И всё равно пространство поисков, изученное в поисках суммы кубов, дающих такое число, как 33, настолько огромно, что даже такие улучшения не могут помочь суперкомпьютерам близко подступиться к этой задаче.
Тут на сцену и вышел Эндрю Букер. Он разработал некоторые дополнительные техники, используя алгебру и теорию чисел, для ещё более сильного улучшения поисковой эффективности. Напустив суперкомпьютер своего университета на эту задачу, через три недели он получил впервые найденное представление числа 33 как суммы трёх кубов:
33 = 8 866 128 975 287 528 3 + (−8 778 405 442 862 239) 3 + (−2 736 111 468 807 040) 3
Решив эту задачу, перед тем, как перейти к числу 3, Букер и Сазерленд решили такую же задачу для числа 42:
42 = (−80 538 738 812 075 974) 3 + 80 435 758 145 817 515 3 + 12 602 123 297 335 631 3
Вас может удивить, что спустя тысячи лет, мы ещё можем узнать что-то новое о таких числах, как 3, 33 и 42. Возможно ещё более удивительным будет то, что этому могут помочь такие абстрактные вещи из школьной математики, как формула для суммы кубов. Однако так работает математика, и поэтому мы продолжаем наши изыскания. Так что следите за числом 114 – самым маленьким из чисел на сегодня, для которого пока ещё не найдена сумма из трёх кубов. У меня есть ощущение, что для Эндрю Букера и других математиков поиск уже начался.
Разность квадратов, сумма и разность кубов — справочник студента
В алгебре разность кубов, как и любая другая формула сокращенного умножения, является тождеством, то есть может быть использована как для перехода из левой части к правой, так и для перехода в обратном направлении.
Произведение разности двух выражений и неполного квадрата их суммы равно разности квадратов этих выражений. Соответственно, получаем правило для разложения разности кубов на множители.
На практике, однако, условие подробно не расписывают. Значит, прежде чем применить формулу разности кубов, надо сначала ее увидеть.
Чтобы найти, сколько знаков нужно поставить после запятой, если известен куб числа, надо количество знаков после запятой в кубе числа разделить на 3.
У 0,008 после запятой стоит три знака, значит, у числа, которое возвели в куб, знаков после запятой в три раза меньше — один. У 0,000000001 — 9 знаков после запятой. Делим девять на 3.
У числа, которое возводят в куб, после запятой — три знака:
Формулы сокращённого умножения. Разность кубов и сумма кубов. Видеоурок. Алгебра 7 Класс
На данном уроке мы продолжим изучать формулы сокращенного умножения, а именно рассмотрим формулы разности и суммы кубов. Кроме того, мы решим различные типовые задачи на применение данных формул.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Упрощение выражений»
При изучении формул сокращенного умножения мы уже изучили:

Выведем формулу разности кубов.
Наша задача – доказать, что при раскрытии скобок в правой части и приведении подобных слагаемых мы придем в результате к левой части.
Выполняем умножение многочленов:
Выполняем умножение многочленов:
Домашнее задание
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
Сумма и разность кубов
Выражение отличается от правой части формулы квадрата разности только коэффициентом при Поэтому это выражение называют неполным квадратом разности.
Читают: сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности.
Разность кубов
Заменив в формуле суммы кубов на получим формулу разности кубов:
Выражение называют неполным квадратом суммы.
Читают: разность кубов двух выражений равна произведению разности этих выражений на неполных квадрат их суммы.
Пример 1. Разложить на множители многочлен
Решение. Заметим, что 

Формулы сокращенного умножения и другие полезные алгебраические тождества
Комментарий репетитора по математике:
Перед вами базовый школьный комплект формул, изучаемый в 7 классе по всем программам. Наибольшая доля задач в учебниках приходится на применение первых трех формул.
Трехчлены и называются неполными квадратами суммы и разности соответственно
Из методики репетитора по заучиванию названий: Примите к сведению, что названия всех формул даются по самой короткой их части.
Например, в формуле разность квадратов это левая часть, а в формуле квадрат суммы — правая. В начале названия формулы указывается последнее действие в этой короткой части.
Дополнительные формулы, изучаемые в математических классах:
Другие полезные алгебраические тождества:
выражение суммы квадратов двух чисел через их сумму
выражение суммы квадратов двух чисел через их разность
Комментарий репетитора по математике: Эти тождества часто используются составителями конкурсных задач по математике (в том числе и на ЕГЭ) для того, чтобы замаскировать в уравнениях и неравенствах замену переменной. Если в вашем задании присутствует сумма квадратов двух выражений попробуйте перейти к сумме или к разности.
Формулы сокращённого умножения
При расчёте алгебраических многочленов для упрощения вычислений используются формулы сокращенного умножения. Всего таких формул семь. Их все необходимо знать наизусть.
Следует также помнить, что вместо «a» и «b» в формулах могут стоять как числа, так и любые другие алгебраические многочлены.
Разность квадратов
Разность квадратов двух чисел равна произведению разности этих чисел и их суммы.
Квадрат суммы
Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа.
(a + b)2 = a2 + 2ab + b2
Обратите внимание, что с помощью этой формулы сокращённого умножения легко находить квадраты больших чисел, не используя калькулятор или умножение в столбик. Поясним на примере:
Помните, что формула квадрат суммы также справедлива для любых алгебраических многочленов.
Предостережение!
(a + b)2 не равно (a2 + b2)
Квадрат разности
Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого на второе плюс квадрат второго числа.
(a − b)2 = a2 − 2ab + b2
Также стоит запомнить весьма полезное преобразование:
Формула выше доказывается простым раскрытием скобок:
(a − b)2 = a2 −2ab + b2 = b2 − 2ab + a2 = (b − a)2 Запомните!
Куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.
(a + b)3 = a3 + 3a2b + 3ab2 + b3
Запомнить эту «страшную» на вид формулу довольно просто.
Предостережение!
(a + b)3 не равно a3 + b3
Куб разности
Куб разности двух чисел равен кубу первого числа минус утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого числа на квадрат второго минус куб второго.
(a − b)3 = a3 − 3a2b + 3ab2 − b3
Запоминается эта формула как и предыдущая, но только с учётом чередования знаков «+» и «−». Перед первым членом «a3 » стоит «+» (по правилам математики мы его не пишем). Значит, перед следующим членом будет стоять «−», затем опять «+» и т.д.
(a − b)3 = + a3 − 3a2b + 3ab2 − b3 = a3 − 3a2b + 3ab2 − b3
Сумма кубов
Не путать с кубом суммы!
Сумма кубов равна произведению суммы двух чисел на неполный квадрат разности.
a3 + b3 = (a + b)(a2 − ab + b2)
Сумма кубов — это произведение двух скобок.
Разность кубов равна произведению разности двух чисел на неполный квадрат суммы.
a3 − b3 = (a − b)(a2 + ab + b2)
Будьте внимательны при записи знаков.
Применение формул сокращенного умножения
Таблицу со всеми формулами сокращённого умножения вы можете скачать в разделе «Шпаргалки».
Формулы сокращенного умножения
Откровенно говоря, эти формулы должен помнить любой ученик седьмого класса. Изучать алгебру даже на школьном уровне и не знать формулу разности квадратов или, скажем, квадрата суммы, просто невозможно.
Они постоянно встречаются при упрощении алгебраических выражений, при сокращении дробей и даже могут помочь в арифметических вычислениях. Ну, например, вам нужно вычислить в уме: 3,162 — 2 • 3,16 • 1,16 + 1,162.
Если вы начнете считать это «в лоб», получится долго и скучно, а если воспользуетесь формулой квадрата разности, ответ получите за 2 секунды!
Итак, семь формул «школьной» алгебры, которые должны знать все:
| Название | Формула |
| Квадрат суммы | (A + B)2 = A2 + 2AB + B2 |
| Квадрат разности | (A — B)2 = A2 — 2AB + B2 |
| Разность квадратов | (A — B)(A + B) = A2 — B2 |
| Куб суммы | (A + B)3 = A3 + 3A2B + 3AB2+ B3 |
| Куб разности | (A — B)3 = A3 — 3A2B + 3AB2 — B3 |
| Сумма кубов | A3 + B3 = (A + B)(A2 — AB + B2) |
| Разность кубов | A3 — B3 = (A — B)(A2 + AB + B2) |
Обратите внимание: никакой формулы суммы квадратов не существует! Не позволяйте своей фантазии заходить слишком далеко.
Как проще всего запомнить все эти формулы? Ну, скажем, увидеть определенные аналогии. Например, формула квадрата суммы похожа на формулу квадрата разности (отличие лишь в одном знаке), а формула куба суммы — на формулу куба разности. Далее, в составе формул разности кубов и суммы кубов мы видим нечто похожее на квадрат суммы и квадрат разности (только коэффициента 2 не хватает).
Но лучше всего эти формулы (как и любые другие!) запоминаются на практике. Решайте больше примеров на упрощение алгебраических выражений, и все ф-лы запомнятся сами собой.
Любознательным школьникам будет, вероятно, интересно обобщить приведенные факты. Вот, скажем, существуют формулы квадрата и куба суммы. А что, если рассмотреть выражения типа (A + B)4, (A + B)5 и даже (A + B)n, где n — произвольное натуральное число? Можно ли увидеть здесь какую — либо закономерность?
Да, подобная закономерность существует. Выражение вида (A + B)n называется биномом Ньютона.
Я рекомендую пытливым школьникам самим вывести формулы для (A + B)4 и (A + B)5, а далее попытаться увидеть общий закон: сравнить, например, степень соответствующего бинома и степень каждого из слагаемых, которые получаются при раскрытии скобок; сравнить степень бинома с количеством слагаемых; попытаться найти закономерности в коэффициентах. Мы не будем сейчас углубляться в эту тему (для этого нужен отдельный разговор!), а лишь запишем готовый результат:
(A + B)n = An + Cn1An-1B + Cn2An-2B2 + … + CnkAn-kBk + … + Bn.
Напоминаю, что n! — это 1 • 2 • … • n — произведение всех натуральных чисел от 1 до n. Называется это выражение факториалом числа n. Например, 4! = 1 • 2 • 3 • 4 = 24. Факториал нуля считается равным единице!
А что можно сказать по поводу разности квадратов, разности кубов и т. п.? Существует ли здесь какая-либо закономерность? Можно ли привести общую формулу для An — Bn?
Да, можно. Вот эта формула:
An — Bn = (A — В)(An-1 + An-2B + An-3B2 + … + Bn-1).
Более того, для нечетных степеней n существует аналогичная ф-ла и для суммы:
An + Bn = (A + В)(An-1 — An-2B + An-3B2 — … + Bn-1).
Мы не будем сейчас выводить эти формулы (кстати, это не очень сложно), но знать об их существовании, безусловно, полезно.
Урок 30. сумма кубов. разность кубов — Алгебра — 7 класс — Российская электронная школа
1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Разложите многочлен на множители:
Произведение делится на 50, так как первый множитель делится на 50: (150 : 50 = 3). Нет необходимости считать значение выражения в скобках. Утверждение доказано.