Докажите что сумма квадратов трех простых чисел больших трех есть число составное

Задачи с решениями. Простые числа

Задачи с решениями. Простые числа. Предлагается 15 задач с подробными решениями.

Просмотр содержимого документа
«Задачи с решениями. Простые числа»

Задачи с решениями. Простые числа

Решение:

Решение:

3.Может ли сумма двух простых чисел быть простым числом?

Решение: Да, может, но при условии, что одно из этих чисел будет равно 2, иначе мы получим сумму двух нечётных чисел, которая в результате будет чётным числом, следовательно, делится на 2 и не является простым.

4.Может ли сумма двух последовательных натуральных чисел быть простым числом?

Решение: 2+3=5, 3+4=7, 5+6=11, 6+7=13, 8+9=17; 5, 7, 11, 13, 17 – простые числа;

Попробуем показать это в общем виде:

Пусть n и n+1 два последовательных натуральных числа, значит одно из них чётное и делится на 2. Тогда их сумма будет равна n+n+1 = 2n+1.

Если n2 и n – чётное, то после сокращения n на 2 получится число, большее одного. Тогда данная сумма будет равна произведению двух чисел, больших 1 и меньших её самой (одно из них – это (n+1), другое то, что получилось после сокращения n на 2). Значит, эта сумма не может быть простым числом, так как имеет делители, отличные от 1 и самой себя.

Аналогично рассматривается случай, когда n2 и n – нечётное. (В этом случае, (n+1) – чётное и большее 2.)

Остались два возможных случая: n=1 и n=2. Если n=1, то сумма будет равна 2n+1 = 2?1+1 = 3 – простое число. Если n=2, то 2n+1= 2?2+1=5 – тоже простое число.

Ответ. На основании этого можно сказать, что сумма двух последовательных натуральных чисел может оказаться простым числом

5.Может ли сумма трёх последовательных натуральных чисел быть простым числом?

Решение: Проведём рассуждения в общем виде:

Пусть n, n+1и n+2 – три последовательных натуральных числа, тогда их сумма равна n+(n+1)+(n+2) = 3n+3 = 3(n+1), т.е. всегда делится на 3, следовательно, составное число.

Ответ. Нет, не может, т.к. полученная сумма является составным числом.

6.Может ли сумма четырех последовательных натуральных чисел быть простым числом?

Решение: Пусть n, n+1и n+2 и n+3 – четыре последовательных натуральных числа, тогда их сумма равна n+(n+1)+(n+2)+( n+3) = 4n+6 = 2(2n+3), т.е. всегда делится на 2, следовательно, составное число.

Ответ. Нет, не может, т.к. полученная сумма является составным числом.

7.Может ли любое натуральное число быть представлено в виде произведения простых чисел?

Решение: Разложим число n, где n – составное число и 16≤ n

Вывод: Из данного разложения замечаем, что любое указанное n может быть представлено в виде произведения, не более трёх простых множителей.

Возникает вопрос: любое ли натуральное число представимо в виде произведения простых множителей?

Ответ на поставленный вопрос даёт основная теорема арифметики:

Всякое натуральное число n1 либо просто, либо может быть представлено, и притом единственным образом, в виде произведения простых множителей.

8.Может ли площадь квадрата, длина стороны которого выражена натуральным числом, быть простым числом?

Ответ. Нет, не может.

9.Клиент банка забыл четырёхзначный шифр своего сейфа и помнил лишь, что этот шифр – простое число, а произведение его цифр равно 243. За какое наименьшее число попыток он наверняка сможет открыть свой сейф.

Решение: Пусть abcd – искомое число. Разложим число 243 на простые множители: 243 = 3?3?3?3?3. Тогда возможны несколько случаев:

243 = 3?3?3?9, но тогда число, составленное из этих цифр будет делиться на 3 (по признаку делимости, сумма цифр равна 18, а 18 делится на 3), значит оно составное;

Из четырех цифр 1,3,9,9 можно составить следующие комбинации: 1399, 1993, 1939, 3991, 3199, 3919, 9139, 9193, 9319, 9391, 9913, 9931. По условию задачи числа должны оказаться простыми. Пользуясь таблице простых чисел, оставляем только простые числа: 1993, 1399, 3919, 9931, 9319, 9391. Остаётся 6 простых чисел, это и есть число попыток, за которое клиент банка сможет открыть сейф.

Ответ. За 6 попыток.

10..Вася умножил некоторое число на 10 и получил простое число. А Петя умножил то же самое число на 15, но всё равно получил простое число. Может ли быть так, что никто из них не ошибся?

Решение: 0,2· 10 = 2 и 0,2·15 = 3 – простые числа.

11.Четверо ребят обсуждали ответ к задаче. Коля сказал: «Это число 9». Роман: «Это простое число». Катя: «Это четное число». А Наташа сказала, что это число делится на 15. Один мальчик и одна девочка ответили верно, а двое остальных ошиблись. Какой ответ в задаче на самом деле?

Решение

Если Коля ответил верно, то обе девочки ошиблись, так как число 9 нечётное и не делится на 15. Значит, верный ответ дал Роман. Но простое число не делится на 15, а единственное чётное простое число – это 2.

12. Докажите, что для произвольного натурального числа n найдётся натуральное m такое, что nm + 1 – составное число.

Решение: Можно выбрать m = n + 2, тогда

nm + 1 = n(n + 2) + 1 = n 2 + 2n + 1 = (n + 1) 2

является составным числом.

13. Найдите все целые числа n, для которых модуль значения трёхчлена n 2 – 7n + 10 будет простым числом.

Решение: Так как |n 2 – 7n + 10| = |n –2| · |n – 5|,

то следует искать такие n при которых один из множителей последнего произведения равен 1, а второй является простым числом.

Этому требованию удовлетворяют n = 3 и n = 4.

14.Доказать, что каждое простое число вида 4k + 1 является длиной гипотенузы прямоугольного треугольника, стороны которого выражаются натуральными числами.

Замечание. Другие примеры подобных троек можно найти в таблице пифагоровых чисел с наибольшим числом не превосходящим 110 и в таблице примитивных пифагоровых чисел со средними числами, не превосходящими 256.

15.Сколькими способами можно раскрасить круг, разбитый на р равных секторов с помощью n красок, если р – простое число и каждый сектор раскрашиваем одной краской? Две раскраски, совпадающие при повороте круга, считаем одинаковыми.

Решение: Каждый сектор можно раскрасить в любой из n цветов, поэтому для круга с р секторами получим n p раскрасок, среди которых (n p – n) не одноцветных. Каждая из этих раскрасок поворотами переходит в (р – 1) одинаковую с ней, значит, существенно различных не одноцветных раскрасок будет (n p – n)/p, откуда общее число раскрасок равно n + (n p – n)/p.

Источник

Докажите что сумма квадратов трех простых чисел больших трех есть число составное

Задача 15:

Найдите остатки от деления

а) 1989 • 1990 • 1991 + 1992³ на 7;

Решение:

Ответ: а) 0; б) 1, так как 9 дает остаток 1 при делении на 8.

Задача 16:

Докажите, что n³ + 2n делится на 3 для любого натурального n.

Решение:

Число n может давать при делении на 3 один из трех остатков: 0, 1, 2. Рассмотрим три случая.

Если n дает остаток 0, то и n³ и 2n делятся на 3 и поэтому n³ + 2n также делится на 3.

Если n дает остаток 1, то n³ дает остаток 1, 2n – остаток 2, а 1 + 2 делится на 3.

Если n дает остаток 2, то n² дает остаток 1, n³ – остаток 2, 2n – остаток 1, а 2 + 1 делится на 3.

Задача 17:

Докажите, что n 5 + 4n делится на 5 при любом натуральном n.

Решение:

Указание: Переберите остатки от деления на 5.

Задача 18:

Докажите, что n² + 1 не делится на 3 ни при каком натуральном n.

Решение:

Переберите остатки от деления на 3.

Задача 19:

Докажите, что n³ + 2 не делится на 9 ни при каком натуральном n.

Решение:

Переберите остатки от деления на 9.

Задача 20:

Докажите, что n³ – n делится на 24 при любом нечетном n.

Решение:

Указание: Докажите, что указанное число делится и на 3, и на 8.

Задача 21:

а) Докажите, что p² – 1 делится на 24, если p – простое число и p > 3.

б) Докажите, что p² – q² делится на 24, если p и q – простые числа, большие 3.

Решение:

Указание: Докажите, что указанные числа делятся и на 3 и на 8.

Задача 22:

Натуральные числа x, y, z таковы, что x² + y² = z². Докажите, что хотя бы одно из этих чисел делится на 3.

Решение:

Если ни x, ни y не делятся на 3, то x² и y² дают остаток 1 от деления на 3. Таким образом, их сумма имеет остаток 2 от деления на 3. Но z² не может иметь такого остатка.

Задача 23:

a и b – натуральные числа, причем число a² + b² делится на 21. Докажите, что оно делится и на 441.

Решение:

Проверьте, что и a и b делятся и на 3 и на 7.

Задача 24:

a, b, c – натуральные числа, причем a + b + c делится на 6. Докажите, что a³ + b³ + c³ тоже делится на 6.

Решение:

Проверьте, что числа x³ и x имеют одинаковые остатки от деления на 6.

Задача 25:

Три простых числа p, q и r, большие 3, образуют арифметическую прогрессию: p = p, q = p + d, r = p + 2d. Докажите, что d делится на 6.

Решение:

Если d – нечетно, то среди чисел p и q есть четное, что невозможно. Если d не делится на 3, то среди чисел p, q и r есть делящееся на 3, что тоже невозможно.

Задача 26:

Докажите, что сумма квадратов трех натуральных чисел, уменьшенная на 7, не делится на 8.

Решение:

Выясните возможные остатки квадратов при делении на 8.

Задача 27:

Сумма трех натуральных чисел, являющихся точными квадратами, делится на 9. Докажите, что из них можно выбрать два, разность которых также делится на 9.

Решение:

Возможные остатки квадратов от деления на 9: 0, 1, 4, 7. Проверьте, что если сумма трех из них делится на 9, то среди них есть два одинаковых.

Задача 28:

Решение:

Так как при нахождении последней цифры очередной степени числа 9 достаточно умножить на 9 лишь последнюю цифру предыдущей степени, то ясно, что за 9 следует 1 (9 • 9 = 81), а за 1 – 9 (1 • 9 = 9).

Таким образом, нечетные степени девятки оканчиваются на 9. Поэтому последняя цифра числа 1989 1989 – девятка.

Задача 29:

Решение:

Выпишем последние цифры нескольких начальных степеней двойки: 2, 4, 8, 6, 2, …. Мы видим, что 2 5 так же, как и 2¹, оканчивается на 2. Поскольку очередная цифра полностью определяется последней цифрой предыдущей степени, то произойдет «зацикливание»: 2 6 (как и 2²) оканчивается на 4, 2 7 (как и 2³) – на 8, 2 8 – на 6, 2 9 – на 2 и т.д. Поскольку длина цикла равна 4, то последняя цифра числа 2 50 определяется остатком от деления числа 50 на 4. Так как он равен 2, то последняя цифра числа 2 50 совпадает с последней цифрой числа 2², то есть равна 4.

Задача 30:

Решение:

Задача 31:

Найдите остаток от деления 2¹ºº на 3.

Решение:

Выпишите остатки от деления на 3 нескольких начальных степеней двойки. Докажите, что здесь происходит «зацикливание».

Задача 32:

Найдите остаток от деления 3 1989 на 7.

Решение:

Задача 33:

Докажите, что 2222 5555 + 5555²²²² делится на 7.

Решение:

Вычислите остаток от деления этого числа на 7 и убедитесь, что он равен нулю.

Задача 34:

Найдите последнюю цифру числа .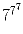

Задача 35:

а) p, p + 10, p + 14 – простые числа. Найдите p.

б) p, 2p + 1, 4p + 1 – простые числа. Найдите p.

Решение:

Рассмотрите остатки от деления на 3. Одно из этих чисел делится на 3. а) p = 3; б) p = 3.

Задача 36:

p и 8p² + 1 – простые числа. Найдите p.

Решение:

Задача 37:

p и p² + 2 – простые числа. Докажите, что p³ + 2 – также простое число.

Решение:

Задача 38:

Докажите, что не существует натуральных чисел a и b таких, что a² – 3b² = 8.

Решение:

Рассмотрите остатки по модулю 3.

Задача 39:

а) Может ли сумма квадратов двух нечетных чисел быть квадратом целого числа?

б) Может ли сумма квадратов трех нечетных чисел быть квадратом целого числа?

Решение:

Проверьте, что остаток квадрата нечетного числа от деления на 4 равен 1, а остаток квадрата четного числа – 0.

Задача 40:

Докажите, что сумма квадратов пяти последовательных натуральных чисел не является точным квадратом.

Решение:

Проверьте, что остаток квадрата нечетного числа от деления на 4 равен 1, а остаток квадрата четного числа – 0.

Задача 41:

p, 4p² + 1 и 6p² + 1 – простые числа. Найдите p.

Ответ: p = 5. Рассмотрите остатки при делении на 5.

Задача 42:

Докажите, что число 100 … 00500 … 001 (в каждой из двух групп по 100 нулей) не является кубом целого числа.

Решение:

Это число дает остаток 7 от деления на 9.

Задача 43:

Докажите, что a³ + b³ + 4 не является кубом целого числа ни при каких натуральных a и b.

Решение:

Выясните, какой остаток может давать число a³ + b³ + 4 от деления на 9.

Задача 44:

Докажите, что число 6n³ + 3 не является шестой степенью целого числа ни при каком натуральном n.

Решение:

Выясните, какой остаток может давать число 6n³ + 3 от деления на 7.

Задача 45:

x, y, z – натуральные числа, причем x² + y² = z². Докажите, что xy делится на 12.

Решение:

Если ни одно из чисел x, y не делится на 3, то z² дает остаток 2 при делении на 3, что невозможно. Заметьте теперь, что квадрат нечетного числа при делении на 8 дает остаток 1, квадрат четного числа, не делящегося на 4, – остаток 4, квадрат числа, делящегося на 4, – остаток 0. Докажите, что либо x и y оба четны, либо среди них есть число, кратное 4.

Источник

math4school.ru

Простые и составные числа

Немного теории

Простое число – это натуральное число, имеющее ровно два различных натуральных делителя: единицу и само себя. Все остальные натуральные числа, кроме единицы, называются составными. Таким образом, все натуральные числа больше единицы разбиваются на простые и составные. Изучением свойств простых чисел занимается теория чисел.

Приведём некоторые свойства простых чисел.

Основная теорема арифметики. Каждое натуральное число, большее единицы, представимо в виде произведения простых чисел, причём единственным способом с точностью до порядка следования сомножителей.

Простых чисел бесконечно много.

Если p – простое, и p делит a·b, то p делит a или b.

Mалая теорема Ферма. Если p – простое, a – натуральное, то a p – a делится на p.

Теорема Вильсона. Натуральное p > 1 является простым тогда и только тогда, когда (p – 1)! + 1 делится на p.

Постулат Бертрана. Если n > 1 – натуральное, то существует простое p, такое, что n 1 – целые взаимно простые числа, содержит бесконечно много простых чисел.

Теорема Ферма. Каждое простое число вида 4k + 1 есть сумма двух квадратов натуральных чисел.

Всякое простое число, большее 3, представимо в виде 6k + 1 или 6k – 1, где k – некоторое натуральное число.

Число, следующее за простым, не может быть квадратом или более высокой степенью с основанием, большим 2.

Число, предшествующее простому, не может быть кубом или более высокой нечётной степенью с основанием, большим 1.

Задачи с решениями

1. Три простых числа, каждое из которых больше 10, образуют арифметическую прогрессию. Докажите, что разность прогрессии делится на 6.

Все данные простые числа нечётные, поэтому их разность делится на 2. Покажем, что она делится и на 3. Пусть данные числа a, a + d, a + 2d. Ни одно из них не делится на 3, поэтому при делении на 3 даёт остаток или 1, или 2. Следовательно, по крайней мере, два из этих чисел дают при делении на 3 одинаковые остатки. Разность этих чисел, равная d или 2d, делится на 3. Поскольку 2 на 3 не делится, то d делится на 3. Итак, разность прогрессии, которая делится на взаимно простые числа 2 и 3, делится на 6, что и требовалось доказать.

2. Докажите, что для произвольного натурального числа n найдётся натуральное m такое, что nm + 1 – составное число.

Можно выбрать m = n + 2, тогда

nm + 1 = n(n + 2) + 1 = n 2 + 2n + 1 = (n + 1) 2

является составным числом.

3. Найдите все целые числа n, для которых модуль значения трёхчлена n 2 – 7n + 10 будет простым числом.

|n 2 – 7n + 10| = |n –2| · |n – 5|,

то следует искать такие n при которых один из множителей последнего произведения равен 1, а второй является простым числом. Этому требованию удовлетворяют n = 3 и n = 4.

4. Докажите, что если числа

а) m и m 2 + 2 простые, то число m 3 + 2 тоже простое;

б) р, р – 10, р + 10 простые, то число р – 2 тоже простое.

а) Любое простое число m, отличное от 3, можно представить в виде 3n+1 или в виде 3n–1, где n – некоторое натуральное число. В первом случае можно записать

m 2 + 2 = 9n 2 + 6n +3,

m 2 + 2 = 9n 2 – 6n +3,

Так как m > 2, то в любом случае число m 2 +2 больше 3 и делится на 3, а значит является составным. Следовательно, число m 2 +2 может быть простым, только если m = 3. В этом случае m 2 +2 = 11 – простое число, m 3 +2 = 29 – тоже простое число, что и требовалось доказать.

б) Так как р – 10 = (р – 1) – 9 и р + 10 = (р + 1) + 9, то числа р – 10 и р – 1 при делении на 3 имеют одинаковые остатки, и числа р + 10 и р + 1 при делении на 3 имеют одинаковые остатки.

Из трёх последовательных чисел р – 1, р, р + 1 одно и только одно делится на 3. С учётом выше сказанного, то же утверждение верно для чисел р – 10, р, р + 10. Так как эти числа простые, то р – 10 = 3 и р = 13, поэтому р – 2 = 11 – простое число, что и требовалось доказать.

5. Сколько раз входит двойка в разложение на простые множители произведения

Ответ на поставленный вопрос получим из следующих преобразований:

6. Найдите все простые p такие, что число p 2 + 11 имеет ровно 6 различных делителей (включая единицу и само число).

Если p > 5 и простое, то числа p – 1 и p + 1 оба четные, и одно из них кратно трем. Поэтому произведение (p – 1)(p + 1) делится на 12, следовательно, p 2 + 11 также делится на 12, а значит, имеет не менее семи делителей (6 делителей числа 12 и само число p 2 + 11 > 12 ). Осталось проверить p = 2 и p = 3.

Если p = 2, то p 2 + 11 = 2 2 + 11 = 15 имеет 4 делителя (1, 3, 5, 15).

Если p = 3, то p 2 + 11 = 3 2 + 11 = 20 имеет 6 делителей (1, 2, 4, 5, 10, 20).

7. Найти все натуральные числа n, для которых каждое из шести чисел

n + 1, n + 3, n + 7, n + 9, n + 13 и n + 15

Рассмотрим варианты. Для n = 1 число n + 3 = 4 составное.

Для n = 2 число n + 7 = 9 составное.

Для n = 3 число n + 1 = 4 составное.

Для n > 4 все наши числа больше 5 и по крайней мере одно из них делится на 5, так как числа 1, 3, 7, 9, 13 и 15 при делении на 5 дают соответственно остатки 1, 3, 2, 4, 3 и 0, то есть все возможные остатки, откуда следует, что и числа

n + 1, n + 3, n + 7, n + 9, n + 13 и n + 15

при делении на 5 дают все возможные остатки и, следовательно, хотя бы одно из них делится на 5 и как число, большее пяти (так как n > 4), является составным.

Но для n = 4 мы получаем простые числа 5, 7, 11, 13, 17 и 19.

8. Доказать, что каждое простое число вида 4k + 1 является длиной гипотенузы прямоугольного треугольника, стороны которого выражаются натуральными числами.

9. Сколькими способами можно раскрасить круг, разбитый на р равных секторов с помощью n красок, если р – простое число и каждый сектор раскрашиваем одной краской? Две раскраски, совпадающие при повороте круга, считаем одинаковыми.

Каждый сектор можно раскрасить в любой из n цветов, поэтому для круга с р секторами получим n p раскрасок, среди которых (n p – n) не одноцветных. Каждая из этих раскрасок поворотами переходит в (р – 1) одинаковую с ней, значит, существенно различных не одноцветных раскрасок будет (n p – n)/p, откуда общее число раскрасок равно n + (n p – n)/p.

10. Доказать, что для любого простого числа p > 5 уравнение х 4 + 4 x = p в целых числах не имеет решений.

Докажем, что если для некоторого целого значения х число

является целым, то это число либо не превосходит пяти, либо является составным.

Действительно, если х 4 + 4 0 4 + 4 1 = 5.

Если x = 2k (k – натуральное число), то число

f(x) = 2 4 k 4 + 4 2k = 2 4 ( k 4 + 4 2(k–1) )

Наконец, если x = 2k + 1 (k – натуральное число), то число

f(x) = x 4 + 4·4 2k = (x 4 + 4x 2 (2 k ) 2 + 4(2 k ) 4 ) – 4x 2 (2 k ) 2 =

= (x 2 + 2(2 k ) 2 ) 2 – (2·x·2 k ) 2 =

= (x 2 + 2·x·2 k + 2(2 k ) 2 )·( x 2 – 2·x·2 k + 2(2 k ) 2 ) =

= ((x + 2 k ) 2 + 2 2k )·((x – 2 k ) 2 + 2 2k )

так же является составным, поскольку каждый из двух сомножителей последнего произведения больше 1 (ибо 2 2k > 1 при k > 0).

Таким образом, если число p > 5 простое, то равенство х 4 + 4 x = p не выполняется ни при каких целых значениях х.

Задачи без решений

1. Известно, что р, р + 10, р + 14 – простые числа. Найдите число р.

2. Докажите, что число

3. Найдите все простые р для которых число р 2 + 14 так же будет простым числом.

4. Докажите, что уравнение х 2 + х + 1 = р·у имеет решение в целых числах (х, у) для бесконечного числа простых р.

5. Введём обозначение для суммы первых n простых чисел через S_n:

Докажите, что между числами S_n и S_n+1 всегда существует число, являющееся полным квадратом.

Источник

Представление чисел суммой двух квадратов и эллиптические кривые

Совсем легко понять, почему 3, 7, 11 и прочие числа, дающие при делении на 4 остаток 3, непредставимы в виде a 2 +b 2 : квадрат чётного числа всегда делится на 4, квадрат нечётного числа всегда даёт остаток 1 при делении на 4, сумма двух квадратов при делении на 4 может давать остатки 0, 1 или 2, но никак не 3. Представимость простых чисел вида 4k+1 неочевидна (особенно если заметить, что простота существенна: число 21 хотя и имеет нужный остаток, но суммой двух квадратов не представляется).

Вычеты

Натуральных чисел бесконечно много. Бывает полезно объединять их в классы по каким-нибудь признакам. В частности, объединение по остатку от деления на какое-нибудь число n приводит к вычетам по модулю n: вычет x̅ — это класс всех чисел, которые при делении на n дают тот же остаток, что и x. Что эквивалентно, вычет x̅ состоит из всех чисел вида x+n∙k, где k целое. В рамках данного поста все вычеты будут по модулю p (того самого нечётного простого числа из введения). Естественно, различных вычетов столько же, сколько может быть остатков от деления на p, то есть ровно p. По сравнению с бесконечностью натуральных чисел переход к вычетам сильно сокращает число вариантов.
Операции над классами далеко не всегда имеют смысл. Например, попытка сложить класс простых чисел с классом составных чисел не очень осмысленна: мы умеем складывать только числа, а у суммы простого числа и составного числа не видно свойств, общих для класса. Хотя члены клуба тавтологии и могут сказать, что сложение класса простых чисел и класса составных чисел даёт класс чисел, раскладывающихся в сумму простого числа и составного числа.

Для вычетов, тем не менее, сложение, вычитание и умножение, «унаследованные» от натуральных чисел, дают другие вычеты. Например, 2̅+3̅=5̅: возьмём любое число с остатком 2, любое число с остатком 3, и их сумма обязательно даст остаток 5. Вообще говоря, произведение двух ненулевых вычетов по произвольному модулю может внезапно оказаться нулём, 2̅∙3̅=0̅ по модулю 6, что неприятно. Но в случае простого модуля, очевидно, такого не бывает, как говорят, нет делителей нуля. Кроме того, можно решить уравнение a̅∙x̅=b̅ (операция деления) для любых двух вычетов, кроме случая a̅=0̅, и результат будет однозначно определён. Однозначность следует из того, что произведение ненулевых вычетов ненулевое. Поскольку a̅≠0̅, то наибольший общий делитель a и p равен 1 (здесь тоже нужна простота p), расширенный алгоритм Евклида найдёт x и y такие, что a∙x+p∙y=1, откуда следует a̅∙x̅=1̅, а значит, a̅∙(b̅∙x̅)=b̅.

Важное следствие из отсутствия делителей нуля: ненулевой многочлен от одной переменной степени n не может иметь более n корней. (Это хорошо известно для обычных целых чисел, но при использовании операций над вычетами требует дополнительного обоснования: уравнение 3̅∙x̅=0̅ по модулю 6 имеет три решения 0̅, 2̅, 4̅.) Действительно, обычное деление «в столбик» показывает, что любой многочлен f(x) можно представить в виде f(x)=(x-с)g(x)+(некоторая константа), где многочлен g(x) имеет степень на единицу меньше; если c — это корень f(x), то константа равна нулю (подставим x=c); если c’ — другой корень f(x), то он будет корнем g(x) (здесь важно отсутствие делителей нуля), так что процесс можно продолжить. Если уже набралось n корней, то оставшийся g(x) будет константой, причём ненулевой (иначе f(x)=0) и больше корней не имеет.

Вычеты по простому модулю можно складывать, вычитать, умножать. На ненулевые вычеты можно делить. Все эти операции обладают обычными свойствами типа a̅∙b̅=b̅∙a̅. В умных книгах говорят, что вычеты по простому модулю образуют поле (а вычеты по составному модулю, где делить нельзя, а всё остальное такое же, — коммутативное кольцо). И не надо быть умной книгой, чтобы назвать это поле конечным. Поле вычетов — не единственное конечное поле, но другие конечные поля нам не понадобятся.

Чуть-чуть про эллиптические кривые

Квадратичные вычеты и невычеты

Теперь мы готовы предъявить обещанные формулы для компонентов разложения p в сумму двух квадратов. Теорема. Пусть g — любой квадратичный невычет. Если p при делении на 4 даёт остаток 1, то

причём число в первой скобке целое нечётное, число во второй скобке целое чётное. Если же p при делении на 4 даёт остаток 3, то обе суммы в скобках нулевые (а значит, число точек на эллиптических кривых равно p+1).

Доказательство

Поскольку пост и без того длинный, доказательство убрано под спойлер. Его можно спокойно пропустить без ущерба для восприятия.

Если взять ненулевой вычет c и умножить его на все вычеты от 1̅ до p̅-1̅, все произведения будут ненулевыми и попарно различными (если c∙x=c∙y, то c∙(x-y)=0̅, что при ненулевом c может быть только если x=y), а значит, это будет просто какая-то перестановка всех вычетов от 1̅ до p̅-1̅. Следовательно, 1̅∙2̅∙. ∙(p̅-1̅)=(c∙1̅)∙(c∙2̅)∙. ∙(c∙(p̅-1̅))=c p-1 ∙1̅∙2̅∙. ∙(p̅-1̅) и c p-1 =1̅ для любого ненулевого вычета c. (Это было доказательство малой теоремы Ферма.)

Как следствие, получаем .

Если p даёт остаток 1 при делении на 4, то слагаемые с x и -x равны и их сумма четна. Значит, вся сумма также четна и числа в скобках действительно целые. Чётность/нечётность после деления пополам ненамного сложнее: в первой скобке теоремы есть три нулевых слагаемых, остальные слагаемые разбиваются на (p-3)/2 пар с суммой ±2 в каждой паре; при любом знаке при делении на 4 получается остаток 2, вся сумма при делении на 4 даёт остаток такой же, как p-3, то есть 2. После деления пополам получим нечётное число. Во второй скобке теоремы всего одно нулевое слагаемое и (p-1)/2 пар с ±2, итоговый остаток от деления на 4 получается 0, после деления пополам остаётся чётное число.

Пусть p при делении на 4 даёт остаток 1. Обозначим первую скобку теоремы через a, вторую через b. Мы уже знаем, что a и b целые.

Итак, первый способ вычисления даёт

Если x₂/x₁ — квадратичный невычет, то аналогично эллиптическим кривым число решений равно 2p минус число решений в случае квадратичного вычета, то есть 2p-(p-1)=p+1.

Суммируем. Есть один вариант с x₁=x₂=0, дающий p решений. Есть 2(p-1) вариантов, где один из x нулевой, а другой ненулевой, каждый из вариантов даёт p решений. Есть 2(p-1) вариантов с x₂=±x₁, каждый из которых даёт 2p-1 решений. Есть (p-1)((p-1)/2-2) вариантов, где x₁ — произвольный ненулевой вычет, а x₂/x₁ — квадратичный вычет, отличный от ±1̅, каждый из этих вариантов даёт p-1 решений. Наконец, остаётся (p-1) 2 /2 вариантов, где x₁ — произвольный ненулевой вычет, а x₂/x₁ — квадратичный невычет, в каждом из этих вариантов p+1 решений. Итого .

Сравнение двух выражений для N завершает доказательство.

Причём здесь криптография?

Знание числа точек на кривой важно для криптографии на этой кривой. На эллиптической кривой можно ввести операцию сложения точек (о чём слышали, наверное, все, кто хоть что-то знает о криптографии) со специальной точкой O в роли нуля. На основе операции сложения можно определить умножение на натуральное число: 2P=P+P, 3P=P+P+P и так далее. Так вот, можно доказать, что если n — порядок кривой, то nP=O для любой точки P. Зная n, c, d, можно решать уравнения вида x∙(cP)=dP полностью аналогично делению вычетов: расширенный алгоритм Евклида найдёт x, y такие, что c∙x+n∙y=1, откуда x∙(cP)+y∙(nP)=P, то есть x∙(cP)=P. При этом, если c, d неизвестны, а cP и dP заданы координатами, то эффективных методов деления в общем случае неизвестно.

Вычислить число точек на заданной кривой довольно сложно (полиномиальный алгоритм существует, но на практике довольно медленный). Чтобы построить кривую с какими-нибудь свойствами на число точек, можно пытаться взять случайные коэффициенты и вычислять число точек в цикле, пока не получится то, что надо, но придётся подождать. К счастью, есть другой способ.

Источник