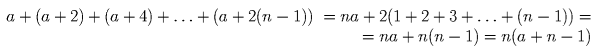Докажите что сумма n последовательных натуральных чисел является составным числом

Докажите что сумма n последовательных натуральных чисел является составным числом

Задача 46:

а) a + 1 делится на 3. Докажите, что 4 + 7a делится на 3.

б) 2 + a и 35 – b делятся на 11. Докажите, что a + b делится на 11.

Решение:

Указания: а) 4 + 7a = 4(a + 1) + 3a; б) a + b = (2 + a) – (35 – b) + 33.

Задача 47:

Найдите последнюю цифру числа 1² + 2² + … + 99².

Решение:

Задача 48:

Про семь натуральных чисел известно, что сумма любых шести из них делится на 5. Докажите, что каждое из данных чисел делится на 5.

Решение:

Докажите, что любые два числа из этих семи дают одинаковый остаток от деления на 5. Для этого рассмотрите две шестерки: одну – не содержащую первое из них, вторую – не содержащую второе.

Задача 49:

Докажите, что сумма n последовательных нечетных натуральных чисел при n > 1 является составным числом.

Решение:

Обозначим первое из этих чисел через a. Получим

Задача 50:

Найдите наименьшее число, дающее следующие остатки: 1 – при делении на 2, 2 – при делении на 3, 3 – при делении на 4, 4 – при делении на 5, 5 – при делении на 6.

Решение:

Заметим, что это число, увеличенное на 1, делится на 2, 3, 4, 5, 6. Ответ: 59.

Задача 51:

Докажите, что если (n – 1)! + 1 делится на n, то n – простое число.

Решение:

Если n – составное число (n > 4), то (n – 1)! делится на n.

Задача 52:

Докажите, что существует такое натуральное n, что числа n + 1, n + 2, …, n + 1989 – составные.

Решение:

Попробуем рассказать, как можно придти к решению. Число n + 1 должно быть составным. Попытаемся пойти по самому простому пути: сделаем так, чтобы n + 1 делилось на 2. n + 2 также должно быть составным, но делиться на 2 уже не может. Попытаемся опять пойти по самому простому пути: хотелось бы сделать так, чтобы n + 2 делилось на 3. Продолжая в том же духе, можно пытаться найти число n такое, что n + 1 делится на 2, n + 2 – на 3, n + 3 – на 4 и так далее. Это равносильно тому, что n – 1 делится на 2, 3, 4, …, 1990. Такое число, конечно, существует – например, 1990!. Итак, в качестве искомого n можно взять число 1990! + 1.

Задача 53:

Докажите, что существует бесконечно много простых чисел.

Решение:

Источник

Докажите что сумма n последовательных нечетных натуральных чисел при n&gt ; 1 является составным числом?

Докажите что сумма n последовательных нечетных натуральных чисел при n&gt ; 1 является составным числом.

Сумма n последовательных нечетных натуральных чисел при n&gt ; 1

Доказательство методом математической индукции

Пусть для n = k утверждение выполняется, т.

Докажем, что тогда выполняется утверждение и для n = k + 1, т.

По методому математической индукции формула справедлива.

Число n ^ 2 при n&gt ; 1 zвляется составным, оно делится на 1, n, n ^ 2.

А значит сумма n последовательных нечетных натуральных чисел при n&gt ; 1 является составным числом.

Даны два последовательных нечетных натуральных числа?

Даны два последовательных нечетных натуральных числа.

Сумма первого нечетного числа и удвоенного второго нечетного числа не больше 37.

Найдите наименьшее из этих натуральных нечетных чисел.

Докажите, что сумма любых трех нечетных чисел являются четным числом?

Докажите, что сумма любых трех нечетных чисел являются четным числом.

Докажите, что сумма любых трех последовательных натуральных чисел кратна 3.

Помогите пожалуйста срочно.

Зараннее огромное спасибо.

Докажите что сумма шести последовастельных натуральных чисел всегда нечетна?

Докажите что сумма шести последовастельных натуральных чисел всегда нечетна.

Сумма четырёх натуральных чисел равна 348?

Сумма четырёх натуральных чисел равна 348.

Три числа являются последовательными натуральными числами, четвёртое равно их сумме.

Можно ли написать 10 последовательных натуральных чисел, каждое из которых является составным?

Можно ли написать 10 последовательных натуральных чисел, каждое из которых является составным?

Докажи что значение суумы шести последовательных натуральных чисел нечетное?

Докажи что значение суумы шести последовательных натуральных чисел нечетное.

Сумма пяти последовательных натуральных нечетных чисел равна 9975?

Сумма пяти последовательных натуральных нечетных чисел равна 9975.

1759 получилось, но не уверена.

Цена за 1 кг творога = 140 руб. Если цена повысилась на 20%, то она стала равна 140 + 0, 2 * 140 = 140 + 28 = 168 (руб). 0, 5 кг творога стали стоить 168 : 2 = 84 (руб). 168 рублей стал стоить творог 2)1682 = 84 рубля.

11×3 = 33 33×30 = 990 31 час.

Источник

Докажите что сумма n последовательных натуральных чисел является составным числом

Задача 15:

Найдите остатки от деления

а) 1989 • 1990 • 1991 + 1992³ на 7;

Решение:

Ответ: а) 0; б) 1, так как 9 дает остаток 1 при делении на 8.

Задача 16:

Докажите, что n³ + 2n делится на 3 для любого натурального n.

Решение:

Число n может давать при делении на 3 один из трех остатков: 0, 1, 2. Рассмотрим три случая.

Если n дает остаток 0, то и n³ и 2n делятся на 3 и поэтому n³ + 2n также делится на 3.

Если n дает остаток 1, то n³ дает остаток 1, 2n – остаток 2, а 1 + 2 делится на 3.

Если n дает остаток 2, то n² дает остаток 1, n³ – остаток 2, 2n – остаток 1, а 2 + 1 делится на 3.

Задача 17:

Докажите, что n 5 + 4n делится на 5 при любом натуральном n.

Решение:

Указание: Переберите остатки от деления на 5.

Задача 18:

Докажите, что n² + 1 не делится на 3 ни при каком натуральном n.

Решение:

Переберите остатки от деления на 3.

Задача 19:

Докажите, что n³ + 2 не делится на 9 ни при каком натуральном n.

Решение:

Переберите остатки от деления на 9.

Задача 20:

Докажите, что n³ – n делится на 24 при любом нечетном n.

Решение:

Указание: Докажите, что указанное число делится и на 3, и на 8.

Задача 21:

а) Докажите, что p² – 1 делится на 24, если p – простое число и p > 3.

б) Докажите, что p² – q² делится на 24, если p и q – простые числа, большие 3.

Решение:

Указание: Докажите, что указанные числа делятся и на 3 и на 8.

Задача 22:

Натуральные числа x, y, z таковы, что x² + y² = z². Докажите, что хотя бы одно из этих чисел делится на 3.

Решение:

Если ни x, ни y не делятся на 3, то x² и y² дают остаток 1 от деления на 3. Таким образом, их сумма имеет остаток 2 от деления на 3. Но z² не может иметь такого остатка.

Задача 23:

a и b – натуральные числа, причем число a² + b² делится на 21. Докажите, что оно делится и на 441.

Решение:

Проверьте, что и a и b делятся и на 3 и на 7.

Задача 24:

a, b, c – натуральные числа, причем a + b + c делится на 6. Докажите, что a³ + b³ + c³ тоже делится на 6.

Решение:

Проверьте, что числа x³ и x имеют одинаковые остатки от деления на 6.

Задача 25:

Три простых числа p, q и r, большие 3, образуют арифметическую прогрессию: p = p, q = p + d, r = p + 2d. Докажите, что d делится на 6.

Решение:

Если d – нечетно, то среди чисел p и q есть четное, что невозможно. Если d не делится на 3, то среди чисел p, q и r есть делящееся на 3, что тоже невозможно.

Задача 26:

Докажите, что сумма квадратов трех натуральных чисел, уменьшенная на 7, не делится на 8.

Решение:

Выясните возможные остатки квадратов при делении на 8.

Задача 27:

Сумма трех натуральных чисел, являющихся точными квадратами, делится на 9. Докажите, что из них можно выбрать два, разность которых также делится на 9.

Решение:

Возможные остатки квадратов от деления на 9: 0, 1, 4, 7. Проверьте, что если сумма трех из них делится на 9, то среди них есть два одинаковых.

Задача 28:

Решение:

Так как при нахождении последней цифры очередной степени числа 9 достаточно умножить на 9 лишь последнюю цифру предыдущей степени, то ясно, что за 9 следует 1 (9 • 9 = 81), а за 1 – 9 (1 • 9 = 9).

Таким образом, нечетные степени девятки оканчиваются на 9. Поэтому последняя цифра числа 1989 1989 – девятка.

Задача 29:

Решение:

Выпишем последние цифры нескольких начальных степеней двойки: 2, 4, 8, 6, 2, …. Мы видим, что 2 5 так же, как и 2¹, оканчивается на 2. Поскольку очередная цифра полностью определяется последней цифрой предыдущей степени, то произойдет «зацикливание»: 2 6 (как и 2²) оканчивается на 4, 2 7 (как и 2³) – на 8, 2 8 – на 6, 2 9 – на 2 и т.д. Поскольку длина цикла равна 4, то последняя цифра числа 2 50 определяется остатком от деления числа 50 на 4. Так как он равен 2, то последняя цифра числа 2 50 совпадает с последней цифрой числа 2², то есть равна 4.

Задача 30:

Решение:

Задача 31:

Найдите остаток от деления 2¹ºº на 3.

Решение:

Выпишите остатки от деления на 3 нескольких начальных степеней двойки. Докажите, что здесь происходит «зацикливание».

Задача 32:

Найдите остаток от деления 3 1989 на 7.

Решение:

Задача 33:

Докажите, что 2222 5555 + 5555²²²² делится на 7.

Решение:

Вычислите остаток от деления этого числа на 7 и убедитесь, что он равен нулю.

Задача 34:

Найдите последнюю цифру числа .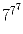

Задача 35:

а) p, p + 10, p + 14 – простые числа. Найдите p.

б) p, 2p + 1, 4p + 1 – простые числа. Найдите p.

Решение:

Рассмотрите остатки от деления на 3. Одно из этих чисел делится на 3. а) p = 3; б) p = 3.

Задача 36:

p и 8p² + 1 – простые числа. Найдите p.

Решение:

Задача 37:

p и p² + 2 – простые числа. Докажите, что p³ + 2 – также простое число.

Решение:

Задача 38:

Докажите, что не существует натуральных чисел a и b таких, что a² – 3b² = 8.

Решение:

Рассмотрите остатки по модулю 3.

Задача 39:

а) Может ли сумма квадратов двух нечетных чисел быть квадратом целого числа?

б) Может ли сумма квадратов трех нечетных чисел быть квадратом целого числа?

Решение:

Проверьте, что остаток квадрата нечетного числа от деления на 4 равен 1, а остаток квадрата четного числа – 0.

Задача 40:

Докажите, что сумма квадратов пяти последовательных натуральных чисел не является точным квадратом.

Решение:

Проверьте, что остаток квадрата нечетного числа от деления на 4 равен 1, а остаток квадрата четного числа – 0.

Задача 41:

p, 4p² + 1 и 6p² + 1 – простые числа. Найдите p.

Ответ: p = 5. Рассмотрите остатки при делении на 5.

Задача 42:

Докажите, что число 100 … 00500 … 001 (в каждой из двух групп по 100 нулей) не является кубом целого числа.

Решение:

Это число дает остаток 7 от деления на 9.

Задача 43:

Докажите, что a³ + b³ + 4 не является кубом целого числа ни при каких натуральных a и b.

Решение:

Выясните, какой остаток может давать число a³ + b³ + 4 от деления на 9.

Задача 44:

Докажите, что число 6n³ + 3 не является шестой степенью целого числа ни при каком натуральном n.

Решение:

Выясните, какой остаток может давать число 6n³ + 3 от деления на 7.

Задача 45:

x, y, z – натуральные числа, причем x² + y² = z². Докажите, что xy делится на 12.

Решение:

Если ни одно из чисел x, y не делится на 3, то z² дает остаток 2 при делении на 3, что невозможно. Заметьте теперь, что квадрат нечетного числа при делении на 8 дает остаток 1, квадрат четного числа, не делящегося на 4, – остаток 4, квадрат числа, делящегося на 4, – остаток 0. Докажите, что либо x и y оба четны, либо среди них есть число, кратное 4.

Источник

Задачи с решениями. Простые числа

Задачи с решениями. Простые числа. Предлагается 15 задач с подробными решениями.

Просмотр содержимого документа
«Задачи с решениями. Простые числа»

Задачи с решениями. Простые числа

Решение:

Решение:

3.Может ли сумма двух простых чисел быть простым числом?

Решение: Да, может, но при условии, что одно из этих чисел будет равно 2, иначе мы получим сумму двух нечётных чисел, которая в результате будет чётным числом, следовательно, делится на 2 и не является простым.

4.Может ли сумма двух последовательных натуральных чисел быть простым числом?

Решение: 2+3=5, 3+4=7, 5+6=11, 6+7=13, 8+9=17; 5, 7, 11, 13, 17 – простые числа;

Попробуем показать это в общем виде:

Пусть n и n+1 два последовательных натуральных числа, значит одно из них чётное и делится на 2. Тогда их сумма будет равна n+n+1 = 2n+1.

Если n2 и n – чётное, то после сокращения n на 2 получится число, большее одного. Тогда данная сумма будет равна произведению двух чисел, больших 1 и меньших её самой (одно из них – это (n+1), другое то, что получилось после сокращения n на 2). Значит, эта сумма не может быть простым числом, так как имеет делители, отличные от 1 и самой себя.

Аналогично рассматривается случай, когда n2 и n – нечётное. (В этом случае, (n+1) – чётное и большее 2.)

Остались два возможных случая: n=1 и n=2. Если n=1, то сумма будет равна 2n+1 = 2?1+1 = 3 – простое число. Если n=2, то 2n+1= 2?2+1=5 – тоже простое число.

Ответ. На основании этого можно сказать, что сумма двух последовательных натуральных чисел может оказаться простым числом

5.Может ли сумма трёх последовательных натуральных чисел быть простым числом?

Решение: Проведём рассуждения в общем виде:

Пусть n, n+1и n+2 – три последовательных натуральных числа, тогда их сумма равна n+(n+1)+(n+2) = 3n+3 = 3(n+1), т.е. всегда делится на 3, следовательно, составное число.

Ответ. Нет, не может, т.к. полученная сумма является составным числом.

6.Может ли сумма четырех последовательных натуральных чисел быть простым числом?

Решение: Пусть n, n+1и n+2 и n+3 – четыре последовательных натуральных числа, тогда их сумма равна n+(n+1)+(n+2)+( n+3) = 4n+6 = 2(2n+3), т.е. всегда делится на 2, следовательно, составное число.

Ответ. Нет, не может, т.к. полученная сумма является составным числом.

7.Может ли любое натуральное число быть представлено в виде произведения простых чисел?

Решение: Разложим число n, где n – составное число и 16≤ n

Вывод: Из данного разложения замечаем, что любое указанное n может быть представлено в виде произведения, не более трёх простых множителей.

Возникает вопрос: любое ли натуральное число представимо в виде произведения простых множителей?

Ответ на поставленный вопрос даёт основная теорема арифметики:

Всякое натуральное число n1 либо просто, либо может быть представлено, и притом единственным образом, в виде произведения простых множителей.

8.Может ли площадь квадрата, длина стороны которого выражена натуральным числом, быть простым числом?

Ответ. Нет, не может.

9.Клиент банка забыл четырёхзначный шифр своего сейфа и помнил лишь, что этот шифр – простое число, а произведение его цифр равно 243. За какое наименьшее число попыток он наверняка сможет открыть свой сейф.

Решение: Пусть abcd – искомое число. Разложим число 243 на простые множители: 243 = 3?3?3?3?3. Тогда возможны несколько случаев:

243 = 3?3?3?9, но тогда число, составленное из этих цифр будет делиться на 3 (по признаку делимости, сумма цифр равна 18, а 18 делится на 3), значит оно составное;

Из четырех цифр 1,3,9,9 можно составить следующие комбинации: 1399, 1993, 1939, 3991, 3199, 3919, 9139, 9193, 9319, 9391, 9913, 9931. По условию задачи числа должны оказаться простыми. Пользуясь таблице простых чисел, оставляем только простые числа: 1993, 1399, 3919, 9931, 9319, 9391. Остаётся 6 простых чисел, это и есть число попыток, за которое клиент банка сможет открыть сейф.

Ответ. За 6 попыток.

10..Вася умножил некоторое число на 10 и получил простое число. А Петя умножил то же самое число на 15, но всё равно получил простое число. Может ли быть так, что никто из них не ошибся?

Решение: 0,2· 10 = 2 и 0,2·15 = 3 – простые числа.

11.Четверо ребят обсуждали ответ к задаче. Коля сказал: «Это число 9». Роман: «Это простое число». Катя: «Это четное число». А Наташа сказала, что это число делится на 15. Один мальчик и одна девочка ответили верно, а двое остальных ошиблись. Какой ответ в задаче на самом деле?

Решение

Если Коля ответил верно, то обе девочки ошиблись, так как число 9 нечётное и не делится на 15. Значит, верный ответ дал Роман. Но простое число не делится на 15, а единственное чётное простое число – это 2.

12. Докажите, что для произвольного натурального числа n найдётся натуральное m такое, что nm + 1 – составное число.

Решение: Можно выбрать m = n + 2, тогда

nm + 1 = n(n + 2) + 1 = n 2 + 2n + 1 = (n + 1) 2

является составным числом.

13. Найдите все целые числа n, для которых модуль значения трёхчлена n 2 – 7n + 10 будет простым числом.

Решение: Так как |n 2 – 7n + 10| = |n –2| · |n – 5|,

то следует искать такие n при которых один из множителей последнего произведения равен 1, а второй является простым числом.

Этому требованию удовлетворяют n = 3 и n = 4.

14.Доказать, что каждое простое число вида 4k + 1 является длиной гипотенузы прямоугольного треугольника, стороны которого выражаются натуральными числами.

Замечание. Другие примеры подобных троек можно найти в таблице пифагоровых чисел с наибольшим числом не превосходящим 110 и в таблице примитивных пифагоровых чисел со средними числами, не превосходящими 256.

15.Сколькими способами можно раскрасить круг, разбитый на р равных секторов с помощью n красок, если р – простое число и каждый сектор раскрашиваем одной краской? Две раскраски, совпадающие при повороте круга, считаем одинаковыми.

Решение: Каждый сектор можно раскрасить в любой из n цветов, поэтому для круга с р секторами получим n p раскрасок, среди которых (n p – n) не одноцветных. Каждая из этих раскрасок поворотами переходит в (р – 1) одинаковую с ней, значит, существенно различных не одноцветных раскрасок будет (n p – n)/p, откуда общее число раскрасок равно n + (n p – n)/p.

Источник

Докажите что сумма n последовательных натуральных чисел является составным числом

Вопрос по математике:

Докажите что сумма n последовательных нечетных натуральных чисел при n>1 является составным числом.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Ответы и объяснения 1

сумма n последовательных нечетных натуральных чисел при n>1

Доказательство методом математической индукции

Пусть для n=k утверждение выполняется, т.е. выполняется

Индукционный переход. Докажем, что тогда выполняется утверждение и для n=k+1, т.е, что выполняется

1+3+5+7+. +(2k-1)+(2K+1)=используем гипотезу МИ=k^2+(2k+1)=k^2+2k+1=используем формлу квадрату двучлена=(k+1)^2, что и требовалось доказать.

По методому математической индукции формула справедлива.

Число n^2 при n>1 zвляется составным, оно делится на 1,n,n^2.

А значит сумма n последовательных нечетных натуральных чисел при n>1 является составным числом. Доказано

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Этого делать не стоит:

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.

Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.

Источник