Докажите что существует бесконечно много простых чисел
Бесконечность множества простых чисел
Одним из свойств простых чисел является утверждение, что множество простых чисел бесконечно, то есть среди простых чисел нет наибольшего. Доказал это свойство Евклид, поэтому его называют теоремой Евклида. При этом он использовал метод от противного.
Доказательство бесконечности множества простых чисел
Предположим обратное – множество простых чисел конечно. Тогда все остальные числа являются составными.
Если множество простых чисел конечно, значит, мы можем перемножить все простые числа между собой. Найдем их произведение и к результату добавим единицу.
Очевидно, полученное число больше любого из простых. Из предположения, что множество простых чисел конечно, следует, что получившееся число составное.
Но если оно составное, то должно при разложении на множители содержать простые сомножители. Однако это не могут быть множители, которые использовались при нахождении этого числа. Ведь к результату была добавлена единица.
Следовательно, произведение уже не делится нацело ни на одно из ранее использованных простых чисел. Потому что будет оставаться остаток 1. Это значит, что должны быть другие простые делители, если уж число действительно составное. Или же само число должно быть простым.
Отсюда приходим к выводу, что всегда найдутся другие простые числа, сколько бы простых чисел мы не использовали для нахождения произведения с последующим добавлением единицы.
2 × 3 × 5 × 7 + 1 = 211. Число 211 само является простым.
2 × 3 × 5 × 7 × 11 × 13 + 1= 30031. Это число делится на 59, которое является простым.
В первом случае произведение простых чисел, сложенное с единицей, само оказалось простым числом. Во втором случае был найден простой делитель, которого не использовался для нахождения произведения.
Таким образом, какой бы исходный список простых чисел не взяли, мы так или иначе найдем новое простое число. Им окажется либо само произведение + 1, либо простое число, которое больше исходных сомножителей, если они были взяты подряд от самого наименьшего простого числа.
5 самых старых нерешенных задач Математики о простых числах
Математика была предметом, который веками бросал вызов величайшим умам в истории человечества. Пожалуй, одной из наиболее исследуемых областей Математики является изучение простых чисел.
Наши размышления о закономерностях в простых числах привели к некоторым сложнейшим проблемам, нерешенным даже величайшими математическими гениями. Сегодня мы рассмотрим 5 старейших математических задач о простых числах, которые интуитивно понятны старшекласснику, но все еще не доказаны даже после упорных попыток в течение 500-2000 лет.
1. Совершенные числа: существуют ли нечетные совершенные числа? Бесконечны ли четные совершенные числа?
Рассмотрим числа 6, 28, 496, 8128…
Что в них особенного? Если вы не знаете, то я бы посоветовал сделать небольшую паузу и попытаться найти красивое свойство, которым обладают эти числа.
Если посмотреть на собственные делители этих чисел, то нетрудно заметить то самое «красивое» свойство:
Числа, для которых сумма собственных делителей равна самому числу, называются совершенными числами. Самое раннее исследование совершенных чисел затеряно в истории. Однако, мы знаем, что пифагорейцы 525годдон.э. изучали совершенные числа.
Что мы знаем о таких числах?
Евклид доказал, что для данного n, если — простое число, то
— совершенное число. В качестве упражнения попробуйте доказать это самостоятельно.
Окей, краткий экскурс.
Простые числа Мерсенна: простые числа вида для некоторого n. Мерсенн предположил, что все числа вида
простые, когда n простое. (Мы знаем, что это неправда. Например,
).
Открытый вопрос: существует ли бесконечно много простых чисел Мерсенна? На данный момент нам известно 47 простых чисел Мерсенна.
В 18 веке Эйлер показал обратное: любое четное совершенное число имеет вид Другими словами, существует взаимно однозначное соответствие между четными совершенными числами и простыми числами Мерсенна.
Как видите, мы знаем о четных совершенных числах и способах их получения еще со времен Евклида около300годдон.э.. Но нам неизвестно, существую ли нечетные совершенные числа. насамомделе,прогрессврешенииэтойпроблемыпрактическиотсутствует.
Подводя итог, можно сказать, что изучение совершенных чисел ставит две давние открытые проблемы, а именно «существование нечетных совершенных чисел» и «существование бесконечно большого числа простых чисел Мерсенна».

2. Гипотеза о близнецах: простых чисел-близнецов бесконечно много
Простые числа-близнецы — это пара вида (p, p + 2), где p и p + 2 являются простыми числами.
Точное происхождение гипотезы о простых числах-близнецах не установлено. Первая формулировка гипотезы о простых числах-близнецах была дана в 1846 году французским математиком Альфонсом де Полиньяком. Однако греческий математик Евклид дал старейшее из известных доказательств существования бесконечного числа простых чисел. Но он не предполагал, что существует бесконечное число простых чисел-близнецов.
На протяжении 2000 лет в доказательстве этого утверждения практически не было прогресса.
Что мы знаем!
Существует бесконечно много простых пар вида (p, p + k), где k = 4 на самом деле является суммой не более чем 6 простых чисел (т.е. С
Дата-центр ITSOFT — размещение и аренда серверов и стоек в двух дата-центрах в Москве. За последние годы UPTIME 100%. Размещение GPU-ферм и ASIC-майнеров, аренда GPU-серверов, лицензии связи, SSL-сертификаты, администрирование серверов и поддержка сайтов.
Докажите что существует бесконечно много простых чисел
Добавить в закладки
Вы сможете увидеть эту публикацию в личном кабинете
Добавить в закладки
Вы сможете увидеть эту публикацию в личном кабинете
Добавить в закладки
Вы сможете увидеть эту публикацию в личном кабинете
Добавить в закладки
Вы сможете увидеть эту публикацию в личном кабинете
Добавить в закладки
Вы сможете увидеть эту публикацию в личном кабинете
Добавить в закладки
Вы сможете увидеть эту публикацию в личном кабинете
Добавить в закладки
Вы сможете увидеть эту публикацию в личном кабинете
Добавить в закладки
Вы сможете увидеть эту публикацию в личном кабинете
Добавить в закладки
Вы сможете увидеть эту публикацию в личном кабинете
Подпишитесь на нашу рассылку и получайте новости о последних проектах, мероприятиях и материалах ПостНауки
Закономерности простых чисел. Гипотеза Римана
 |
В 1859 году немецкий математик Бернхард Риман взял давнюю идею Эйлера и развил ее совершенно по-новому, определив так называемую дзета-функцию. Одним из результатов этой работы стала точная формула для количества простых чисел до заданного предела. Формула представляла собой бесконечную сумму, но специалистам по анализу к этому не привыкать. И это не было бесполезной игрой ума: благодаря этой формуле удалось получить новые подлинные знания о мире простых чисел. Мешала только одна маленькая неувязка. Хотя Риман мог доказать, что его формула точна, самые важные потенциальные следствия из нее полностью зависели от одного простого утверждения, касающегося дзета-функции, и вот это то простое утверждение Риман никак не мог доказать. И сегодня, полтора столетия спустя, мы все еще не сумели сделать это. Сегодня это утверждение называется гипотезой Римана и представляет собой, по сути, священный Грааль чистой математики.
Теорема о распределении простых чисел была ответом на евклидову теорему о том, что простые числа уходят в бесконечность и могут быть сколь угодно большими. Другая фундаментальная евклидова теорема говорит о единственности разложения на простые множители: каждое положительное целое число есть произведение простых чисел, причем только одного их набора. В 1737 году Эйлер понял, что первую теорему можно переформулировать в виде поразительной формулы из действительного анализа, и тогда второе утверждение становится простым следствием этой формулы. Для начала я представлю формулу, а затем попытаюсь разобраться в ней. Вот она:
Здесь принимает все простые значения, а — константа. Эйлера интересовал в основном случай, при котором — целое число, но его формула работает и для действительных чисел, в случае если больше единицы. Это условие необходимо для того, чтобы ряд в правой части сошелся, т. е., будучи продолжен до бесконечности, принял бы осмысленное значение.
Это необыкновенная формула. В левой части мы перемножаем бесконечно много выражений, которые зависят только от простых чисел. В правой — складываем бесконечное число выражений, которые зависят от всех положительных целых чисел. Эта формула выражает, на языке анализа, некоторое отношение между целыми и простыми числами. Главное отношение такого рода — это единственность разложения на простые множители, именно она оправдывает существование формулы.
поэтому взвешенный подсчет дает
Воспользовавшись методами анализа, информацию об этом более хитроумном способе подсчета простых чисел можно превратить в информацию об обычном способе. Однако этот метод приводит к более простым формулам, и присутствие логарифма — не слишком дорогая цена за это. В этих терминах точная формула Римана говорит о том, что взвешенный подсчет до предела эквивалентен
Это заявление о кси-функции эквивалентно аналогичному заявлению о зависимой от нее дзета-функции. А именно: все нетривиальные нули дзета-функции представляют собой комплексные числа вида: они лежат на критической линии «действительная часть равна » (см. рис.). Эта версия замечания и есть знаменитая гипотеза Римана.
 |
Замечание Римана звучит достаточно небрежно, как будто высказано между делом и эта гипотеза не имеет особого значения. И это действительно так, если говорить только о программе Римана по доказательству теоремы о распределении простых чисел. Но во многих других вопросах верно обратное. Многие считают гипотезу Римана важнейшим из остающихся на сегодняшний день открытыми математических вопросов.
Риман так и не довел свою программу до логического конца. Более того, он никогда больше ничего не писал по этому вопросу.
Но два других математика, приняв у него эстафету, показали, что догадка Римана верна. В 1896 году Жак Адамар и Шарль-Жан де ла Валле Пуссен независимо друг от друга вывели теорему о распределении простых чисел, доказав, что все нетривиальные нули дзета-функции лежат в пределах критической полосы. Доказательства у обоих получились очень сложными и техничными, но тем не менее свою задачу они выполнили. Возникла новая мощная область математики — аналитическая теория чисел. Применение ей нашлось в самых разных уголках теории чисел: с ее помощью решали давние задачи и выявляли новые закономерности. Другие математики позже нашли несколько более простых доказательств теоремы о числе простых, а Атле Сельберг и Пал Эрдеш открыли даже очень сложное доказательство, вовсе не требовавшее применения комплексного анализа. Но к тому моменту при помощи идеи Римана было доказано бесчисленное множество важных теорем, включая аппроксимации многих функций теории чисел. Так что это новое доказательство хоть и добавило в эту историю каплю иронии, но ни на что, в сущности, не повлияло. В 1980 году Дональд Ньюман нашел гораздо более простое доказательство, для которого достаточно оказалось всего лишь одной из самых базовых теорем комплексного анализа — теоремы Коши.
Хотя Риман объявил свою гипотезу ненужной для достижения ближайших целей, оказалось, что она жизненно необходима для разрешения многих других вопросов теории чисел. Прежде чем обсуждать гипотезу Римана, нам стоит взглянуть на некоторые теоремы, которые — если бы гипотеза была доказана — из нее следуют.
Из гипотезы Римана можно получить немало других оценок для функций теории чисел. К примеру, из нее прямо следует, что сумма делителей меньше
Но подлинное значение гипотезы Римана куда глубже. Существуют далеко идущие обобщения и сильное подозрение, что тот, кто сумеет доказать гипотезу Римана, сможет, вероятно, доказать и связанную с ней обобщенную гипотезу Римана. А это, в свою очередь, даст математикам власть над обширными областями теории чисел.
Прочерки указывают на то, что соответствующее число не простое.
Доказать, что простых чисел вида тоже бесконечно много, гораздо сложнее, — это можно сделать, но лишь при помощи некоторых достаточно сложных теорем. Разница в подходах обусловлена тем, что любое число вида имеет делитель того же вида, а в отношении чисел вида это не всегда верно.
Кстати говоря, на любой из подобных вопросов нетрудно выдвинуть разумное предположение — простые числа в арифметической последовательности. Случай с достаточно типичен. Эксперимент быстро показывает, что числа приведенных выше четырех видов имеют примерно равные шансы оказаться простыми. Вот похожая таблица:
Так что должно существовать бесконечное количество простых чисел каждого вида, и в среднем к каждому виду должна относиться четверть всех простых чисел до заданного предела.
Для римановой дзета-функции важен не только ряд, но и его аналитическое продолжение, придающее функции значения во всех комплексных точках.
Имеется множество косвенных свидетельств того, что гипотеза Римана — как оригинальная, так и обобщенная — справедлива. Много хорошего следовало бы из истинности этих гипотез. Ни одно из этих следствий за все время не удалось опровергнуть, а ведь сделать это — то же самое, что опровергнуть гипотезу Римана. Но ни доказательства, ни опровержения пока нет. Широко распространено мнение, что доказательство оригинальной гипотезы Римана открыло бы дорогу и к доказательству обобщенного ее варианта. Но на самом деле, возможно, лучше было бы атаковать сразу обобщенную гипотезу Римана во всей ее грозной красе — воспользоваться всем арсеналом доступных на сегодняшний день методов, доказать, а затем вывести оригинальную гипотезу Римана как ее частный случай.
Сегодня у исследователей появился новый стимул к борьбе за доказательство гипотезы Римана: крупный приз.
Многие представители математической науки считают правильным, что в их области не присуждается Нобелевская премия. В настоящее время она составляет чуть больше миллиона долларов, а такая сумма легко может исказить цели исследователей и породить споры о приоритетах. Однако отсутствие крупной математической премии также может исказить представления общества о значимости и полезности этой науки. Можно подумать, что открытия, за которые никто не хочет платить, не так уж важны. Возможно, поэтому не так давно появились две очень престижные новые математические премии. Одна из них — Абелевская — присуждается ежегодно Норвежской академией науки и словесности и названа в честь великого норвежского математика Нильса Хенрика Абеля. Вторая награда — это премии за решение семи «проблем тысячелетия», объявленные Математическим институтом Клэя. Этот институт основали в 1998 году в Кембридже (штат Массачусетс) американский бизнесмен Лэндон Клэй и его жена Лавиния. Лэндон Клэй активно занимается паевыми инвестиционными фондами и при этом любит и уважает математику. Его организация проводит встречи, выделяет гранты на исследования, организует публичные лекции и присуждает ежегодную премию за математические исследования.
Стоит также помнить о том, что гипотезы, даже освященные временем, иногда оказываются ошибочными. Сегодня большинство математиков, судя по всему, считает, что когда-нибудь гипотеза Римана будет доказана. Некоторые, однако, думают, что она, возможно, все-таки неверна, и где-то в дебрях очень больших чисел может скрываться нуль дзета-функции, который не лежит на критической линии. Если такой «контрпример» существует, то он, скорее всего, окажется очень-очень большим.
Однако на переднем крае математики просто мнение стоит немного. Интуиция зачастую очень помогает ученым, но известно немало случаев, когда это замечательное чувство ошибалось. Житейский здравый смысл может лгать, оставаясь при этом и общепризнанным, и здравым. Литтлвуд, один из лучших знатоков комплексного анализа, выразился вполне однозначно: в 1962 году он сказал, что уверен в ошибочности гипотезы Римана, и добавил, что нет никаких мыслимых причин, по которым она была бы верна. Кто прав? Поживем, увидим.
Иэн Стюарт
Emeritus Professor of Mathematics at the University of Warwick, England
Большие гипотезы о простых числах доказаны для небольших числовых систем
Гипотеза о простых числах-близнецах – один из самых важных и сложных вопросов математики. Двое математиков решили параллельную версию этой задачи для небольших числовых систем.
7 сентября два математика опубликовали доказательство варианта одной из известнейших открытых задач математики. Полученный результат открывает новый фронт в изучении гипотезы о простых числах-близнецах, терзающей математиков вот уже более ста лет, и связанной с некоторыми из глубочайших свойств арифметики.
«Мы давно уже буксовали и у нас заканчивались идеи по этой задаче, поэтому естественный восторг вызывает появление у кого-либо новых идей», — сказал Джеймс Майнард, математик из Оксфорда.
Гипотеза о простых числах-близнецах касается пар простых чисел, отличающихся на 2. Близнецами являются числа 5 и 7. И 17 и 19. Гипотеза утверждает, что таких пар среди натуральных чисел существует бесконечное множество. За последнее десятилетие математики добились существенного прогресса, но до полного решения задачи им ещё очень далеко.
Авторы нового доказательства, Уил Савин из Колумбийского университета и Марк Шустерман из Висконсинского университета в Мэдисоне, доказали гипотезу для менее крупного, но всё же заметного математического мира. Они доказали её справедливость в случае конечной числовой системы, в которой есть лишь несколько чисел.
Такие числовые системы называются «конечными полями». Несмотря на их малый размер, они сохраняют множество математических свойств, присущих бесчисленным целым числам. Математики пытаются искать ответы на вопросы арифметики в конечных полях, и надеются транслировать эти результаты на все целые числа.
«Конечная мечта, пусть и немного наивная, заключается в том, что хорошее понимание свойств конечного поля может пролить свет на мир целых чисел», — сказал Майнард.
Кроме доказательства гипотезы о простых числах-близнецах Савин и Шустерман нашли ещё более удивительный результат, касающийся поведения простых чисел в небольших числовых системах. Они доказали, с какой именно частотой простые числа-близнецы появляются на небольших интервалах – и этот результат даёт возможность чрезвычайно точно контролировать такое явление, как простые числа-близнецы. Математики мечтают достичь сходных результатов и с обычными числами; они исследуют новое доказательство в поисках идей, применимых к простым числам на числовой прямой.
Новый вид простых чисел
Самое известное предсказание гипотезы о простых числах-близнецах заключается в наличии бесконечно большого количества пар чисел, различающихся на 2. Однако это утверждение более общее. Оно говорит о том, что существует бесконечное количество простых чисел, различающихся на 4 (к примеру, 3 и 7), или на 14 (293 и 307), или на любое заданное вами число.
Альфонс де Полиньяк сделал это предположение в его современном виде в 1849 году. За последовавшие 160 лет математики не сильно продвинулись с ним. Однако в 2013 году лёд тронулся, или, по крайней мере, серьёзно треснул. В тот год Чжан Итан доказал наличие бесконечно большого количества пар простых чисел, отличающихся друг от друга не более, чем на 70 млн. В следующем году другие математики, включая Мэйнарда и Терри Тао, серьёзно уменьшили этот разрыв. Текущим рекордом служит доказательство существования бесконечно большого количества пар простых чисел, отличающихся друг от друга не более, чем на 246.
Однако после этого прогресс утих. Математики понимают необходимость совершенно новой идеи для полного решения данной задачи. И конечные числовые системы – неплохое место для поисков этой идеи.
Чтобы построить конечное поле, сначала нужно извлечь конечное подмножество чисел из натуральных. Можно, к примеру, взять первые пять чисел (или любое простое количество). И вместо того, чтобы, как обычно, представлять числа на числовой линии, представьте новую числовую систему в виде циферблата.
Арифметика, как вы могли догадаться, начинает работать в замкнутом пространстве. Чему будет равно 4 + 3 в конечной числовой системе, состоящей из пяти элементов? Начнём с 4, отсчитаем три деления по часовой стрелке, и придём к 2. Вычитание, умножение и деление работают сходным образом.
Но только тут есть подвох. На конечных полях не имеет смысла обычное определение простого числа. На конечном поле любое число делится на любое другое. К примеру, 7 обычно не делится на 3. Но на конечном поле из пяти элементов – делится. Всё потому, что на этом конечном поле число 7 эквивалентно числу 12 – они оба заканчиваются на отметке 2 циферблата. Поэтому 7 разделить на 3 даст то же самое, что и 12 разделить на 3 – а 12, делённое на 3, даст 4.
Поэтому гипотеза простых чисел-близнецов для конечных полей относится к простым многочленам – таким математическим выражениям, как, например, x 2 + 1.
Допустим, к примеру, что ваше конечное поле содержит числа 1, 2 и 3. Эти числа будут коэффициентами многочлена в этом конечном поле, а «простым» многочленом будет такой, который нельзя разложить на множители-многочлены. Поэтому x 2 + x + 2 будет простым, поскольку его нельзя разложить на множители, а x 2 — 1 не будет: это произведение (x + 1) и (x − 1).
Определив простые многочлены, естественно задать вопрос о простых многочленах-близнецах – парах многочленов, являющихся простыми, и отличающихся на фиксированное значение. К примеру, многочлен x 2 + x + 2 простой, как и x 2 + 2x + 2. Отличаются они на x.
Гипотеза о простых многочленах-близнецах для конечных полей говорит о существовании бесконечно большого количества пар простых многочленов-близнецов, отличающихся не просто на x, а на любое значение.
Аккуратные разрезы
Понятия конечных полей и простых многочленов могут показаться притянутыми за уши, и бесполезными для изучения свойств чисел. Но они похожи на симулятор урагана – вселенную в себе, дающую идеи по поводу явлений, происходящем в большом мире.
«Между целыми числами и многочленами существует древняя аналогия, позволяющая преобразовывать потенциально крайне сложные задачи, связанные с целыми числами, в задачи, связанные с многочленами, которые тоже потенциально сложны, но, возможно, легче поддаются решению», — сказал Шустерман.
Конечные поля приобрели известность в 1940, когда Андре Вейль, разработал точный способ трансляции арифметики небольших числовых систем в арифметику целых чисел. Вейль использовал эту связь с потрясающими результатами. Он доказал, возможно, самую важную проблему в математике – гипотезу Римана – для случая с набором кривых над конечными полями (эта задача известна под именем геометрической гипотезы Римана). Это доказательство, вместе с набором дополнительных гипотез Вейля сделало конечные поля богатым ландшафтом для математических открытий.
Ключевой идеей Вейля было то, что на конечных полях геометрические техники можно использовать для поиска ответов на вопросы по поводу чисел. «Это особенность конечных полей. Многие задачи, которые вы хотите решить, можно перефразировать геометрически», — сказал Шустерман.
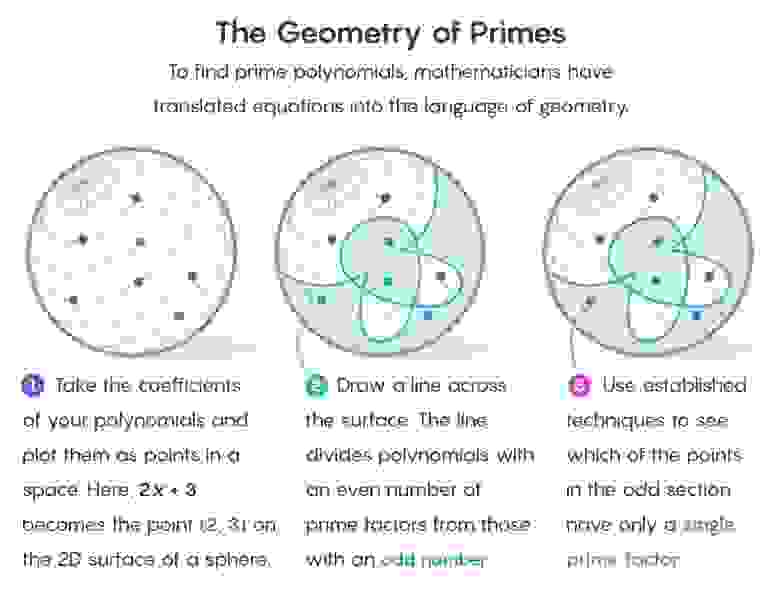
Чтобы понять, как в таком окружении появляется геометрия, представьте себе каждый многочлен в виде точки в пространстве. Коэффициенты многочлена служат координатами, определяющими его местоположение. Возвращаясь к нашему конечному полю из 1, 2 и 3, многочлен 2x + 3 расположится в точке (2, 3) двумерного пространства.
Но даже в простейшем конечном пространстве есть бесконечное множество многочленов. Можно создавать более сложные многочлены, увеличивая показатель самой большой экспоненты, или степень выражения. В нашем случае многочлен x 2 − 3x − 1 будет представлен точкой в трёхмерном пространстве. А многочлен 3x 7 + 2x 6 + 2x 5 − 2x 4 − 3x 3 + x 2 − 2x + 3 будет представлен точкой в восьмимерном пространстве.
В новой работе это геометрическое пространство представляет все многочлены заданной степени для заданного конечного поля. Вопрос превращается в следующий: есть ли способ изолировать все точки, обозначающие простые многочлены?
Стратегия Савина и Шустермана заключается в том, чтобы разделить пространство на две части. В одной части будут все точки, соответствующие многочленам с чётным количеством множителей. В другой – все точки, соответствующие многочленам с нечётным количеством множителей.
Это уже упрощает задачу. Гипотеза простых многочленов-близнецов для конечных полей относится только к многочленам с одним множителем (точно так же, как у простого числа есть один множитель, оно само). И поскольку число 1 нечётное, часть пространства, содержащего многочлены с чётным числом множителей, можно сразу выбросить.
Трюк состоит в использовании деления. В случае с двумерным объектом, например, поверхностью сферы, его разрезает пополам одномерная кривая – так, как экватор разрезает поверхность Земли. Объект с большим числом измерений всегда можно разрезать объектом с числом измерений, меньшим на единицу.
Кривые, нарисованные функцией Мёбиуса, гнутся и извиваются, как бешеные, пересекаясь сами с собою во многих местах. Эти места, называемые сингулярностями, особенно тяжело проанализировать (они соответствуют многочленам, раскладываемым на несколько одинаковых простых множителей).
Принципиальной инновацией Савина и Шустермана было то, что они нашли точный способ разрезать петли с меньшим числом измерений на более короткие отрезки. Эти отрезки было легче изучать, чем петли целиком.
Составив каталог многочленов с нечётным количеством простых множителей – а это было самое трудное — Савин и Шустерман столкнулись с задачей определения того, какие из них простые, и какие – близнецы. Для этого они применили несколько формул, используемых математиками для изучения простых чисел среди обычных.
Савин и Шустерман использовали свою технику, чтобы доказать два важных момента касательно простых многочленов на определённых конечных полях.
Во-первых, гипотеза простых чисел-близнецов на конечных полях верна: существует бесконечно много пар простых многочленов-близнецов, отличающихся на любую заданную величину.
Во-вторых, что более важно, эта работа обеспечивает точный подсчёт количества простых многочленов-близнецов, которые можно найти среди многочленов определённого порядка. Это аналогично знанию о том, сколько простых чисел-близнецов есть внутри любого достаточно длинного интервала на числовой прямой – и это просто мечта математиков.
«Это первая работа, дающая количественную аналогию того, что должно быть истинным для целых чисел, и это реально выдающийся результат, — сказал Зив Рудник из Тель-Авивского университета. – До сих пор ничего подобного не было».
Доказательство Савина и Шустермана показывает, как, спустя почти 80 лет после того, как Андре Вейль доказал гипотезу Римана для кривых над конечными полями, математики всё ещё с упорством движутся в эту сторону. Теперь математики, разбирающиеся с гипотезой простых чисел-близнецов, обратятся к работе Савина и Шустермана, и, возможно, она даст им глубокий источник вдохновения.