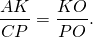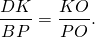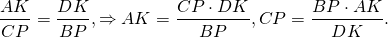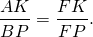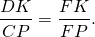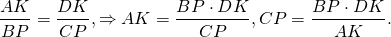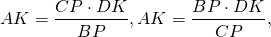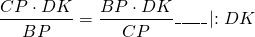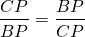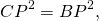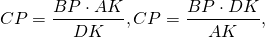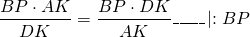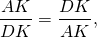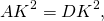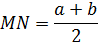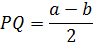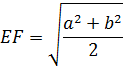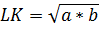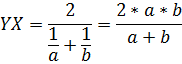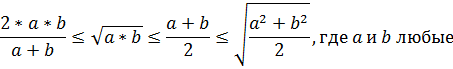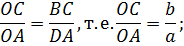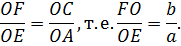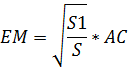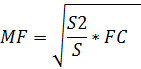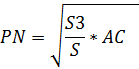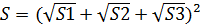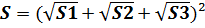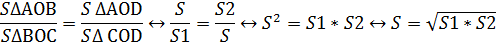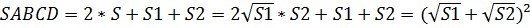Докажите что точка пересечения диагоналей точка пересечения продолжений боковых сторон

Докажите что точка пересечения диагоналей точка пересечения продолжений боковых сторон

Напомним свойства трапеции, которые часто используются при решении задач. Некоторые из этих свойств были доказаны в заданиях для 9-го класса, другие попробуйте доказать самостоятельно. Приведённые рисунки напоминают ход доказательства.

$$ 4.<2>^<○>$$. В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжении боковых сторон, лежат на одной прямой (на рис. 21 точки `M`, `N`, `O` и `K`).

$$ 4.<3>^<○>$$. В равнобокой трапеции углы при основании равны (рис. 22).

$$ 4.<4>^<○>$$. В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции (рис. 23).

$$ 4.<5>^<○>$$. В равнобокой трапеции диагонали равны (рис. 24).

$$ 4.<6>^<○>$$. В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой – их полусумме

(рис. 25, основания равны `a` и `b`, `a>b`).

$$ 4.<7>^<○>$$. Во всякой трапеции середины боковых сторон и середины диагоналей лежат на одной прямой (рис. 26).

$$ 4.<8>^<○>$$. Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований (рис. 27).

Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований, т. е. `d_1^2+d_2^2=c_1^2+c_2^2+2*ab`.

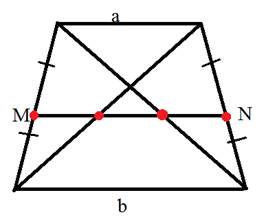
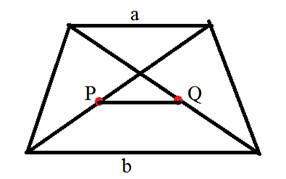
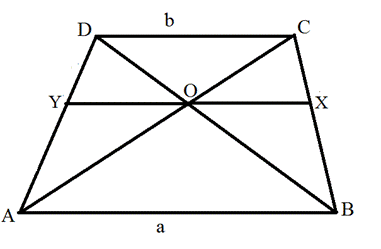
$$ 4.<10>^<○>$$. Во всякой трапеции с основаниями `a` и `b` отрезок с концами на боковых сторонах, проходящий через точку пересечения диагоналей параллельно основаниям, равен `(2ab)/(a+b)` (на рис. 28 отрезок `MN`).

$$ 4.<11>^<○>$$. Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.

Применяем теорему косинусов (см. рис. 29а и б):

`ul(DeltaACD):` `d_1^2=a^2+c_2^2-2a*c_2*cos varphi`,

`ul(DeltaBCD):` `d_2^2=b^2+c_2^2+2b*c_2*cos varphi` (т. к. `cos(180^@-varphi)=-cos varphi`).

Проводим `CK«|\|«BA` (рис. 29в), рассматриваем треугольник `ul(KCD):` `c_1^2=c_2^2+(a-b)^2-2c_2*(a-b)*cos varphi`. Используя последнее равенство, заменяем выражение в скобках в (2), получаем:

В случае равнобокой трапеции `d_1=d_2`, `c_1=c_2=c`, поэтому получаем

Отрезок, соединяющий середины оснований трапеции, равен `5`, одна из диагоналей равна `6`. Найти площадь трапеции, если её диагонали перпендикулярны.

Прямоугольный треугольник `ul(BDK)` с гипотенузой `BK=BC+AD=2MN=10` и катетом `DK=6` имеет площадь `S=1/2DK*BD=1/2DKsqrt(BK^2-DK^2)=24`. Но площадь треугольника `BDK` равна площади трапеции, т. к. если `DP_|_BK`, то

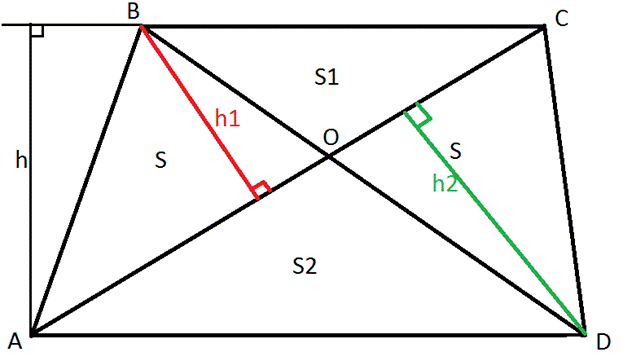
Диагонали трапеции, пересекаясь, разбивают её на четыре треугольника с общей вершиной. Найти площадь трапеции, если площади треугольников, прилежащих к основаниям, равны `S_1` и `S_2`.

Далее, треугольники `BOC` и `DOA` подобны, площади подобных треугольников относятся как квадраты соответствующих сторон, значит, `(S_1)/(S_2)=(a/b)^2`. Таким образом, `(S_0+S_1)/(S_0+S_2)=sqrt((S_1)/(S_2))`.Отсюда находим `S_0=sqrt(S_1S_2)`, и поэтому площадь трапеции будет равна

Основания равнобокой трапеции равны `8` и `10`, высота трапеции равна `3` (рис. 32).

Найти радиус окружности, описанной около этой трапеции.

Из прямоугольного треугольника `ABK` находим `AB=sqrt(1+9)=sqrt(10)` и `sinA=(BK)/(AB)=3/(sqrt10)`. Окружность, описанная около трапеции `ABCD`, описана и около треугольника `ABD`, значит (формула (1), § 1), `R=(BD)/(2sinA)`. Отрезок `BD` находим из прямоугольного треугольника `KDB:` `BD=sqrt(BK^2+KD^2)=3sqrt(10)` (или по формуле `d^2=c^2+ab`), тогда

$$ 4.<12>^<○>$$. Площадь трапеции равна площади треугольника, две стороны которого равны диагоналям трапеции, а третья равна сумме оснований.

Источник

Замечательное свойство трапеции

Замечательное свойство трапеции

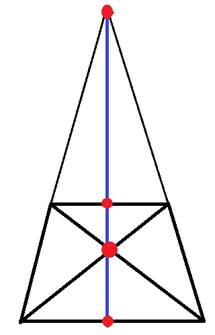
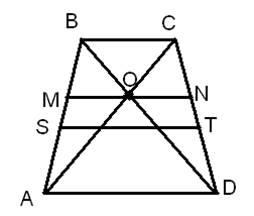
Точка пересечения диагоналей трапеции, точка пересечения продолжения боковых сторон трапеции и середины оснований трапеции лежат на одной прямой.

Существует несколько способов доказательства этого свойства. Надо доказать, что четыре данные точки лежат на одной прямой. Прямую можно провести через любые две точки. Выбирают две любые точки из четырёх, проводят через них прямую и доказывают, что две другие точки также лежат на этой прямой.

Сформулируем это свойство иначе:

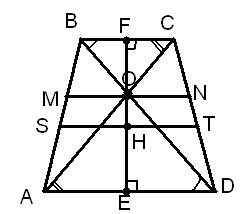
Прямая, проходящая через точку пересечения диагоналей трапеции и точку пересечения продолжения её боковых сторон, делит основания трапеции пополам.

Дано:

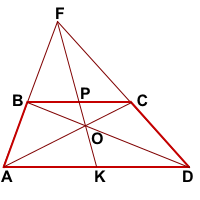
ABCD- трапеция, AD||BC,

Доказать: K- середина AD,

Рассмотрим треугольники AOK и COP.

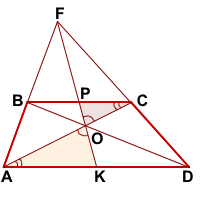
∠OAK=∠OCP (как внутренние накрест лежащие при AD||BC и секущей AC).

Значит, треугольники AOK и COP подобны (по двум углам).

Аналогично, треугольники DOK и BOP подобны и

Так как правые части этих равенств равны, то левые также равны:

Рассмотрим треугольники AFK и BFP.

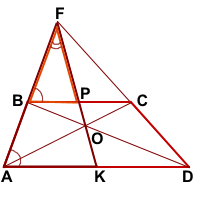
∠KAF=∠PBF (как соответственные при AD||BC и секущей AF).

Следовательно, треугольники AFK и BFP подобны (по двум углам).

Аналогично, треугольники DFK и CFP подобны и

Правые части равенств равны, приравниваем левые части:

а значит, CP=BP, то есть P — середина BC.

AK=DK, K — середина AD.

Что и требовалось доказать.

В нашем случае докажем, что точки O и P лежат на прямой FK.

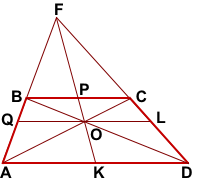
FK — медиана треугольника AFD.

Проведём через точку O пересечения диагоналей трапеции отрезок QL с концами на боковых сторонах трапеции.

BC||AD (как основания трапеции), QL||AD (по построению).

Так как медиана, проведённая к стороне треугольника, делит пополам любой отрезок, параллельный этой стороне, с концами на двух других сторонах треугольника, то точки P и O лежат прямой FK.

Поскольку медиана FK, проведённая к AD, делит пополам любой отрезок, параллельный AD, с концами на сторонах AF и DF, то среднюю линию трапеции она также делит пополам. Таким образом, замечательное свойство трапеции можно дополнить:

Точка пересечения диагоналей трапеции, точка пересечения продолжения боковых сторон трапеции, середины оснований трапеции и середина средней линии трапеции лежат на одной прямой.

Источник

Докажите, что точка пересечения продолжений боковых сторон трапеции, середины оснований и точка пересечения диагоналей лежат на одной прямой.

Из подобия треугольников QBM и QAN следует, что = , а из подобия треугольников QCM и QDN — = . Поэтому = , а т.к. BM = CM, то AN = DN, т.е. N — середина AD.

Аналогично докажем, что прямая, проходящая через точку O пересечения диагоналей и середину одного из оснований, проходит через середину другого основания.

При гомотетии с центром в точке O персечения диагоналей AC и BD, переводящей вершину B трапеции ABCD в вершину D, точка C переходит в точку A, основание BC — в основание DA, середина M основания BC — в середину N основания DA. Следовательно, прямая MN проходит через центр гомотетии, т.е. через точку O.

Аналогично докажем, что прямая MN проходит через точку пересечения прямых AB и DC.

Из подобия треугольников QBM и QAN следует, что = , а из подобия треугольников QCM и QDN — = . Поэтому = , а т.к. BM = CM, то AN = DN, т.е. N — середина AD.

Аналогично докажем, что прямая, проходящая через точку O пересечения диагоналей и середину одного из оснований, проходит через середину другого основания.

При гомотетии с центром в точке O персечения диагоналей AC и BD, переводящей вершину B трапеции ABCD в вершину D, точка C переходит в точку A, основание BC — в основание DA, середина M основания BC — в середину N основания DA. Следовательно, прямая MN проходит через центр гомотетии, т.е. через точку O.

Аналогично докажем, что прямая MN проходит через точку пересечения прямых AB и DC.

Из подобия треугольников QBM и QAN следует, что = , а из подобия треугольников QCM и QDN — = . Поэтому = , а т.к. BM = CM, то AN = DN, т.е. N — середина AD.

Аналогично докажем, что прямая, проходящая через точку O пересечения диагоналей и середину одного из оснований, проходит через середину другого основания.

При гомотетии с центром в точке O персечения диагоналей AC и BD, переводящей вершину B трапеции ABCD в вершину D, точка C переходит в точку A, основание BC — в основание DA, середина M основания BC — в середину N основания DA. Следовательно, прямая MN проходит через центр гомотетии, т.е. через точку O.

Аналогично докажем, что прямая MN проходит через точку пересечения прямых AB и DC.

Источник

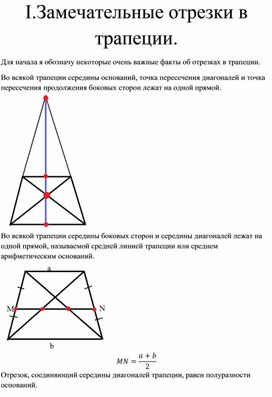
Замечательные свойства трапеции

Для начала я обозначу некоторые очень важные факты об отрезках в трапеции.

1. Во всякой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжения боковых сторон лежат на одной прямой.

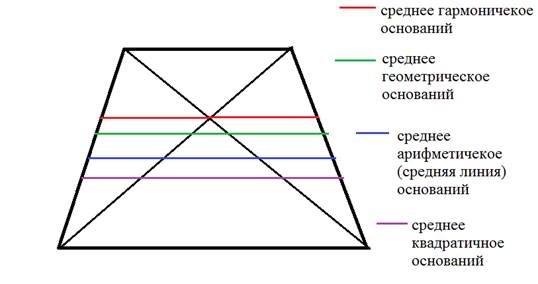
2. Во всякой трапеции середины боковых сторон и середины диагоналей лежат на одной прямой, называемой средней линией трапеции или среднем арифметическим оснований.

3. Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.

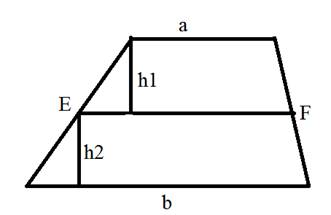
4. Отрезок, параллельный основаниям и разбивающий трапецию на две равновеликие трапеции, равен среднему квадратичному оснований:

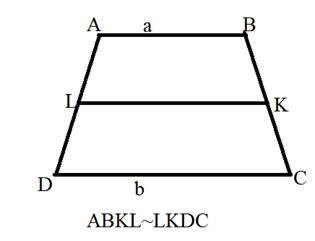
5. Отрезок,разбивающий трапецию на две подобные трапеции, имеет длину, равную среднему геометрическому длин оснований.

6. Отрезок, проходящий через точку пересечения диагоналей параллельно основаниям, равен среднему гармоническому оснований.

Между средними отрезками выполняются следующие соотношения

Доказательства этих фактов я не считаю нужным и уместным приводить в докладе, так как любой уважающий себя школьник должен их знать и уметь делать самостоятельно

Теперь, когда мы знаем эти, весьма важные, факты преступим к решению поистине прекрасных задач.

Применим приём достраивания.

Ответ: не может быть.

∆ DOA (по двум накрестлежащим углам)→

3. Подставляем a =2 b в равенство 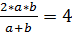, находим b =3 и а=6.

Для того, чтобы решать задачи, где рассматривается площадь трапеции, необходимо помнить несколько очень важных утверждений:

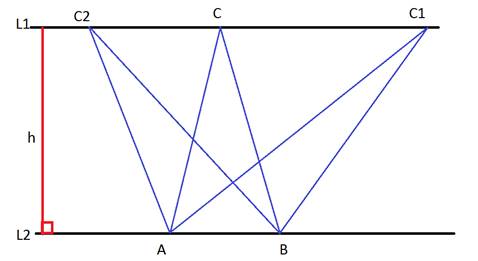
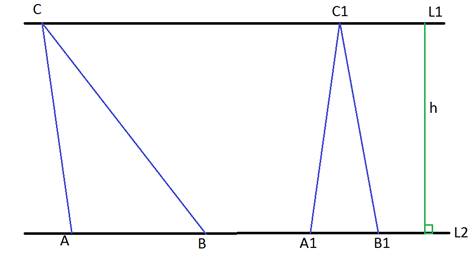
2. Если прямая L 1║ L 2 и треугольники не имеют общегооснования, то

.

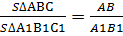
Высоты у этих треугольников равные, следовательно, площади этих треугольников относятся, как их снования.

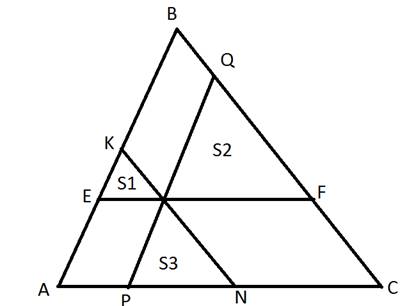
Через точку М, лежащую внутри треугольника АВС проведены три прямые, параллельные его сторонам. При этом образовались три треугольника(см.рис.), площади которых равны S 1, S 2, S 3. Найдите площадь треугольника АВС.

Ответ:

Мне захотелось убедиться, возможно ли в трапеции похожее соотношение площадей. И действительно в трапеции нашёлся похожий случай. Рассмотрим его в следующей задачи.

Дана трапеция ABCD ; в трапеции проведены диагонали, пересекающиеся в точке О. Выразите площадь трапеции из площадей образовавшихся треугольников.

5. Правые части равенств (1) и (2) одинаковы, следовательно одинаковы и правые части:

Ответ: площадь трапеции равна .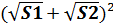

Источник

Трапеция. Свойства трапеции

Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

Свойства трапеции

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.

Коэффициент подобия –

Отношение площадей этих треугольников есть .

4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.

5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.

7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

Свойства и признаки равнобедренной трапеции

1. В равнобедренной трапеции углы при любом основании равны.

2. В равнобедренной трапеции длины диагоналей равны.

3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.

4. Около равнобедренной трапеции можно описать окружность.

5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Вписанная окружность

Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то

Площадь

или где – средняя линия

Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Помогите, пожалуйста
Дана трапеция ABCD (верхнее основание BC меньше AD) с заданной S=27 и (AD/BC)=4/3. Диагонали трапеции пересекаются в точке О. Средняя линия трапеции пересекает диагонали в точке М и N.
а) Докажите, что треугольники АВО и СОD равновелики;
б) Найдите площадь треугольника MNO.

1)

При этом где – высота трапеции.
Потому и
2) Пусть
откуда
Коэффициент подобия треугольников – Тогда и высоты этих треугольников находятся в оношении То есть равны и соответственно.
Высота треугольника

Источник