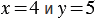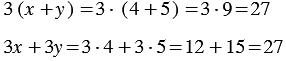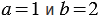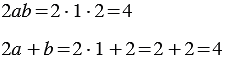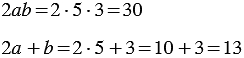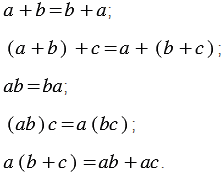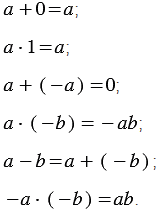Докажите что тождественно равны выражения
Тождественно равные выражения. Тождества
| Два выражения, значения которых равны при любых значениях переменных, называют тождественно равными. |
Рассмотрим две пары выражений:
1) 
Найдем их значения при
Мы получили один и тот же результат. Из распределительного свойства следует, что вообще при любых значениях переменных 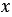
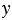

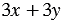
2)
Найдем их значения при
Мы получили один и тот же результат. Однако, можно указать такие значения 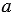
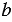
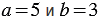
Мы получили разные результаты.
Следовательно, выражения 
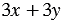
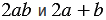
| Равенство, верное при любых значениях переменных, называется тождеством. |
Равенство 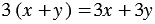
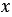
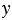
Также к тождествам можно отнести равенства, выражающие свойства сложения и умножения чисел:
Можно привести и другие примеры тождеств:
Тождествами считают и верные числовые равенства.
Очень часто при вычислении значений выражений, легче сначала упростить имеющееся выражение, а затем выполнять вычисления.
| Замену одного выражения другим, тождественно равным ему выражением, называют тождественным преобразованием или просто преобразованием выражения. |
К тождественным преобразованиям можно отнести приведение подобных слагаемых и раскрытие скобок.
Примеры:
1) 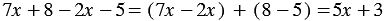
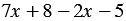
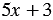
2) 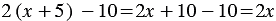
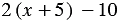
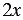
Для того, чтобы доказать, что данное равенство является тождеством (или доказать тождество), используют следующие методы:
1) тождественно преобразуют одну из частей данного равенства, получая другую часть;
2) тождественно преобразуют каждую из частей данного равенства, получая одно и то же выражение;
3) доказывают, что разность левой и правой частей данного равенства тождественно равна нулю.
Также, чтобы доказать, что равенство не является тождеством, достаточно привести контрпример, т.е. указать такое значение переменной (или переменных, если их несколько), при котором данное равенство не выполняется.
Пример: Докажите, что равенство 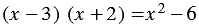
Решение: Приведем контрпример. Если 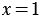
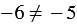
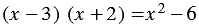
Поделись с друзьями в социальных сетях:
Тождественно равные выражения: определение, примеры
После того, как мы разобрались с понятием тождеств, можно переходить к изучению тождественно равных выражений. Цель данной статьи – объяснить, что это такое, и показать на примерах, какие выражения будут тождественно равными другим.
Тождественно равные выражения: определение
Понятие тождественно равных выражений обычно изучается вместе с самим понятием тождества в рамках школьного курса алгебры. Приведем основное определение, взятое из одного учебника:
Тождественно равными друг другу будут такие выражения, значения которых будут одинаковы при любых возможных значениях переменных, входящих в их состав.
Также тождественно равными считаются такие числовые выражения, которым будут отвечать одни и те же значения.
Это достаточно широкое определение, которое будет верным для всех целых выражений, смысл которых при изменении значений переменных не меняется. Однако позже возникает необходимость уточнения данного определения, поскольку помимо целых существуют и другие виды выражений, которые не будут иметь смысла при определенных переменных. Отсюда возникает понятие допустимости и недопустимости тех или иных значений переменных, а также необходимость определять область допустимых значений. Сформулируем уточненное определение.
Тождественно равные выражения – это те выражения, значения которых равны друг другу при любых допустимых значениях переменных, входящих в их состав. Числовые выражения будут тождественно равными друг другу при условии одинаковых значений.
Фраза «при любых допустимых значениях переменных» указывает на все те значения переменных, при которых оба выражения будут иметь смысл. Это положение мы объясним позже, когда будем приводить примеры тождественно равных выражений.
Можно указать еще и такое определение:
Тождественно равными выражениями называются выражения, расположенные в одном тождестве с левой и правой стороны.
Примеры выражений, тождественно равных друг другу
Используя определения, данные выше, рассмотрим несколько примеров таких выражений.
Для начала возьмем числовые выражения.
Так, 2 + 4 и 4 + 2 будут тождественно равными друг другу, поскольку их результаты будут равны ( 6 и 6 ).
Но область допустимого значения в одном выражении может отличаться от области другого.
Если мы заменяем одно выражение на другое, которое является тождественно равным ему, то этот процесс называется тождественным преобразованием. Это понятие очень важно, и подробно о нем мы поговорим в отдельном материале.
Тождественные преобразования
Содержание
Вспомнить, что такое тождество, вы можете в предыдущей теме.
В обоих примерах были произведены какие-то действия (в первом случае прибавили, во втором – отняли), но прежнее равенство они не нарушили.
В математике тоже можно производить подобные действия над равенствами, и они называются тождественными преобразованиями.
Их главная цель – сделать решение более легким.
Пример тождественного преобразования
Что называют тождественным преобразованием
Замену одного выражения другим, тождественно равным ему, называют тождественным преобразованием выражения.
Часто слово «тождественное» пропускают и в задании просто просят преобразовать выражение.
Приведем еще примеры совсем простых тождественных преобразований:
Все свойства арифметических действий являются примерами тождественных преобразований, например:
То есть, арифметические действия над выражениями, которые вы выполняли ранее, относятся к тождественным преобразованиям выражений.
Например, мы можем записать, что
Как понять, что преобразование было тождественным
Как мы можем доказать, что выполняемые нами действия сделаны по правилам, а преобразование было тождественным? Для этого необходимо следовать одному из следующих алгоритмов:
Логично, что если одно из числовых выражений в равенстве представляет собой число, то для доказательства нужно решить только второе.
Все ли значения можно подставить вместо переменной?
Но любое ли значение для подставления вместо переменной можно брать при доказательстве? Далее вы будете изучать область допустимых значений (ОДЗ) для переменной. При доказательстве мы должны использовать только допустимые ее значения.