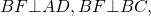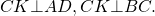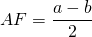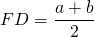Докажите что трапеция равнобедренная если
Если у трапеции углы при основании равны
(I признак равнобедренной трапеции).
Если у трапеции углы при основании равны, то она — равнобедренная.

Доказать: ABCD — равнобедренная.
1) Проведем высоты трапеции BF и CK:
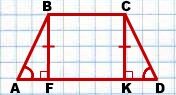
∠AFB=90º, ∠DKC=90º (так как BF и CK — высоты трапеции).
BF=CK (как высоты трапеции).
Следовательно, треугольники ABF и DCK равны (по катету и острому углу).
3) Из равенства треугольников следует равенство соответствующих сторон: AB=CD.
Следовательно, трапеция ABCD — равнобедренная ( по определению).
∠A+∠B=180º (как внутренние односторонние при AD ∥ BC и секущей AB),
∠D+∠C =180º (как внутренние односторонние при AD ∥ BC и секущей CD).
Таким образом, из равенства углов при меньшем основании следует равенство углов и при большем основании трапеции. Уже доказали, что в этом случае трапеция — равнобедренная.
Равнобедренная трапеция
Что такое равнобедренная трапеция и каковы ее свойства?
Равнобедренная трапеция — это трапеция, у которой боковые стороны равны.
Еще равнобедренную трапецию называют равнобокой (или равнобочной) трапецией.
ABCD — равнобедренная трапеция.
AD и BC — основания трапеции,
AB и CD — её боковые стороны,
Перечислим основные свойства равнобедренной трапеции.
Свойства равнобедренной трапеции:

2) Сумма противолежащих углов равнобедренной трапеции равна 180º.

4) Около любой равнобедренной трапеции можно описать окружность.
Кроме основных, у равнобедренной трапеции есть и другие свойства. Например, можно доказать один раз и в дальнейшем использовать при решении задач следующее утверждение:
Высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, а другой — полуразности оснований.

Признаки равнобедренной трапеции:
1) Если углы при основании трапеции равны, то она — равнобедренная.
2) Если сумма противолежащих углов трапеции равна 180º, то она — равнобедренная.
3) Если диагонали трапеции равны, то она — равнобедренная.
4) Если около трапеции можно описать окружность, то она — равнобедренная.
Геометрия. 8 класс
Четырёхугольник, две стороны которого параллельны, а две другие не параллельны, называется трапецией. Параллельные стороны называются основаниями трапеции, непараллельные стороны – боковыми сторонами.
Если один из углов трапеции прямой, то она называется прямоугольной. Если боковые стороны трапеции равны, то она называется равнобедренной трапецией (равнобокой).
Сформулируем и докажем свойства равнобедренной трапеции:
Свойство первое: в равнобедренной трапеции углы при каждом основании равны.
Для доказательства проведём отрезок CK, параллельный AB.
CK || AB, ABCK – параллелограмм (стороны попарно параллельны), значит AB = CK, но AB = CD (трапеция равнобедренная), значит CK = CD, треугольник KCD – равнобедренный,
По свойству равнобедренного треугольника ∠1 = ∠2.
∠2 = ∠3 (соответственные при секущей AD и параллельных AB и CK). Следовательно, ∠1 = ∠3.
ABC = 180° − ∠3 = 180° − ∠1 = ∠BCD.
Второе свойство равнобедренной трапеции: диагонали равнобедренной трапеции равны.
Дано: ABCD – равнобедренная трапеция, BC || AD
Доказать: AC = BD.
Для доказательства рассмотрим треугольники ABC и DCB. Треугольники ABC и DCB равны (AB = CD, BC – общая сторона, ∠ABC = ∠DCA). Следовательно, AC = BD.
Теоремы, обратные свойствам равнобедренной трапеции, также верны. Это признаки равнобедренной трапеции.
Признак первый: если углы при основании трапеции равны, то трапеция является равнобедренной.
Дано: ABCD – трапеция, BC || AD
∠BAC = ∠CDA
Доказать: ABCD – равнобедренная трапеция
Для доказательства проведем отрезок CK, параллельный AB.
Доказательство:
CK || AB, следовательно ABCK – параллелограмм, тогда AB = CK, ∠A = ∠CKD.
Получится равнобедренный треугольник CKD (∠A = ∠CKD и ∠A = ∠CDA), поэтому
CK = CD и AB = CK = CD. Следовательно, ABCD – равнобедренная трапеция.
Второй признак: если диагонали трапеции равны, то трапеция равнобедренная.
Дано: ABCD –трапеция, BC || AD
AC = BD
Доказать: ABCD – равнобедренная трапеция