Докажите что угол треугольника является острым прямым или тупым

Докажите что угол треугольника является острым прямым или тупым

Вопрос 1. Дайте определение косинуса острого угла прямоугольного треугольника.
Ответ. Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
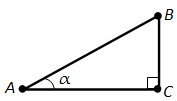
Косинус угла \(\alpha\) обозначается так: \(\cos \alpha\). На рисунке 147 показан прямоугольный треугольник ABC с углом A, равным \(\alpha\). Косинус угла \(\alpha\) равен отношению катета AC, прилежащего к этому углу, к гипотенузе AB, т.е.

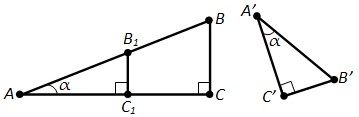
Построим треугольник AB₁C₁, равный треугольнику A’B’C’, как показано на рисунке 148. Так прямые BC и B₁C₁ перпендикулярны прямой AC, то они параллельны. По теореме о пропорциональных отрезках

А так как по построению AC₁ = A’C’, AB₁ = A’B’, то

Вопрос 3. Докажите теорему Пифагора.
Ответ. Теорема 7.2 (теорема Пифагора). В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
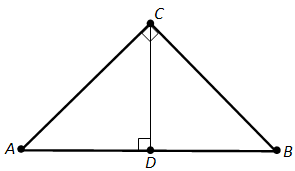
Доказательство.Пусть ABC – данный прямоугольный треугольник с прямым углом C. Проведём высоту CD из вершины прямого угла C (рис. 149).

По определению косинуса угла \(\cos A = \frac = \frac\). Отсюда \(AB \cdot AD = AC^2\). Аналогично \(\cos B = \frac = \frac\). Отсюда \(AB \cdot BD = BC^2\). Складывая полученные равенства почленно и замечая, что \(AD + DB = AB\), получим:

Источник

Тупоугольный треугольник, элементы, свойства, признаки и формулы

Тупоугольный треугольник, элементы, свойства, признаки и формулы.

Тупоугольный треугольник – это треугольник, у которого один угол тупой.

Тупоугольный треугольник (понятие и определение):

Тупоугольный треугольник – это треугольник, у которого один угол тупой, т.е. один из его углов лежит в пределах между 90° и 180°.

Рис. 1. Тупоугольный треугольник

∠ BАC– тупой угол треугольника,

Рис. 2. Равносторонний треугольник

АВ = ВС = АС – стороны треугольника,

Рис. 3. Прямоугольный треугольник

Рис. 4. Равнобедренный треугольник

АВ = AС – боковые стороны, BС – основание,

Хотя в тупоугольном треугольнике тупой угол больше 90 градусов, сумма углов в треугольнике всегда равна 180 градусам.

Элементы тупоугольного треугольника:

Кроме сторон и углов у тупоугольного треугольника также имеются внешние углы. Внешний угол это угол, смежный с внутренним углом треугольника. У любого треугольника, в т.ч. тупоугольного, 6 внешних углов, по 2 на каждый внутренний. Внешний угол тупого угла тупоугольного треугольника всегда будет острым углом. Внешний угол острого угла тупоугольного треугольника всегда будет тупым углом.

Рис. 5. Тупоугольный треугольник и внешний угол

Медиана тупоугольного треугольника (как и любого другого треугольника), соединяющая вершину треугольника с противоположной стороной, делит ее пополам, т.е. на два одинаковых отрезка.

Рис. 6. Тупоугольный треугольник и медиана тупоугольного треугольника

MA – медиана тупоугольного треугольника

Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.

Рис. 7. Тупоугольный треугольник и высота тупоугольного треугольника

MС – высота тупоугольного треугольника

Высота тупоугольного треугольника может лежать за пределами треугольника.

Биссектриса в тупоугольном треугольнике (как и в любом другом треугольнике) делит угол пополам. Биссектрисы пересекаются в точке, которая является центром вписанной окружности.

Рис. 8. Тупоугольный треугольник и биссектриса угла тупоугольного треугольника

MA – биссектриса тупого угла тупоугольного треугольника

Кроме того, биссектриса тупоугольного треугольника (как и любого другого треугольника) делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Свойства тупоугольного треугольника:

Свойства тупоугольного треугольника аналогичны свойствам обычного треугольника:

1. Против большей стороны лежит больший угол, и наоборот.

Рис. 9. Тупоугольный треугольник

2. Против равных сторон лежат равные углы, и наоборот.

Рис. 10. Тупоугольный треугольник с равными боковыми сторонами

3. Сумма углов тупоугольного треугольника равна 180°.

4. Любая сторона тупоугольного треугольника меньше суммы двух других сторон и больше их разности:

Источник