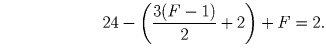Докажите что в плоском графе есть вершина степень которой не превосходит 5
Докажите что в плоском графе есть вершина степень которой не превосходит 5
Задача 17:
В стране Озерная 7 озер, соединенных между собой 10 каналами, причем от любого озера можно доплыть до любого другого. Сколько в этой стране островов?
Решение:
Задача 18:
В квадрате отметили 20 точек и соединили их непересекающимися отрезками друг с другом и с вершинами квадрата так, что квадрат разбился на треугольники. Сколько получилось треугольников?
Решение:
Будем считать отмеченные точки и вершины квадрата вершинами, а соединяющие их отрезки и стороны квадрата – ребрами плоского графа. Для каждого куска, на которые этот граф разбивает плоскость, подсчитаем число ограничивающих его ребер, и все полученные числа сложим. Поскольку каждое ребро разделяет два куска, то в итоге получим удвоенное число ребер. Так как все куски, кроме внешнего – треугольники, а внешний кусок ограничен 4 ребрами, то получаем 3(F – 1) + 4 = 2E, т.е. E = 3(F – 1)/2 + 2. Заметим, что число вершин нашего графа равно 24 и подставим количества вершин и ребер в формулу Эйлера:
Отсюда F = 43. Таким образом, число треугольников, на которые разбился квадрат, равно 42.
Задача 19:
Докажите, что для плоского графа справедливо неравенство 2E ≥ 3F.
Решение:
Указание: каждый кусок ограничивается не менее, чем тремя ребрами.
Задача 20:
Для плоского связного графа справедливо неравенство E ≤ 3V – 6.
Решение:
Из предыдущей задачи известно, что 2E ≥ 3F. Подставим это в формулу Эйлера. Получим V – E + 2E/3 ≥ 2. Отсюда E ≤ 3V – 6, что и требовалось.
Задача 21:
Докажите, что для любого плоского графа (в том числе и несвязного) справедливо неравенство E ≤ 3V – 6.
Решение:
Указание: Требуемое утверждение получается сложением неравенств для компонент связности.
Задача 22:
Граф, имеющий 5 вершин, каждая из которых соединена ребром с любой другой, не является плоским.
Решение:
Указание: Для этого графа не выполнено неравенство E ≤ 3V – 6.
Задача 23:
Можно ли построить три дома, вырыть три колодца и соединить тропинками каждый дом с каждым колодцем так, чтобы тропинки не пересекались?
Решение:
Указание: Для графа из этой задачи неравенство 2E ≥ 3F можно усилить. Поскольку в этом графе каждый кусок должен быть ограничен по меньшей мере 4 ребрами, то рассуждения, аналогичные решению задачи 19, приводят к неравенству E ≥ 2F.
Задача 24:
Докажите, что граф, имеющий 10 вершин, степень каждой из которых равна 5, – не плоский.
Решение:
Не выполняется неравенство 3V – 6 ≥ E.
Задача 25:
Докажите, что в плоском графе есть вершина, степень которой не превосходит 5.
Решение:
Предположим противное. Тогда 2E ≥ 6V, т.е. E ≥ 3V, что противоречит неравенству.
Задача 26:
Каждое ребро полного графа с 11 вершинами покрашено в один из двух цветов: красный или синий. Докажите, что либо «красный», либо «синий» граф не является плоским.
Решение:
Пусть оба эти графа – плоские. Тогда у них вместе не более, чем (3 11 – 6) + (3 11 – 6) = 54 ребра. Однако в полном графе с 11 вершинами 55 ребер. Противоречие.
Задача 27:
Семиугольник разбит на выпуклые пяти- и шестиугольники, причем так, что каждая его вершина является вершиной по крайней мере двух многоугольников разбиения. Докажите, что число пятиугольников разбиения не меньше 13.
Решение:
Докажите сначала неравенство E ≤ 3V – 6, используя то, что из каждой вершины выходит по крайней мере 3 ребра. Обозначим количество пятиугольников через a, количество шестиугольников через b. Заметим, что 5a + 6b + 7 = 2E ≤ 6F – 12 = 6(a + b + 1) – 12. Отсюда a ≥ 13.
Докажите что в плоском графе есть вершина степень которой не превосходит 5
Задача 17:
В стране Озерная 7 озер, соединенных между собой 10 каналами, причем от любого озера можно доплыть до любого другого. Сколько в этой стране островов?
Задача 18:
В квадрате отметили 20 точек и соединили их непересекающимися отрезками друг с другом и с вершинами квадрата так, что квадрат разбился на треугольники. Сколько получилось треугольников?
Задача 19:
Докажите, что для плоского графа справедливо неравенство 2E ≥ 3F.
Задача 20:
Для плоского связного графа справедливо неравенство E ≤ 3V – 6.
Задача 21:
Докажите, что для любого плоского графа (в том числе и несвязного) справедливо неравенство E ≤ 3V – 6.
Задача 22:
Граф, имеющий 5 вершин, каждая из которых соединена ребром с любой другой, не является плоским.
Задача 23:
Можно ли построить три дома, вырыть три колодца и соединить тропинками каждый дом с каждым колодцем так, чтобы тропинки не пересекались?
Задача 24:
Докажите, что граф, имеющий 10 вершин, степень каждой из которых равна 5, – не плоский.
Задача 25:
Докажите, что в плоском графе есть вершина, степень которой не превосходит 5.
Задача 26:
Каждое ребро полного графа с 11 вершинами покрашено в один из двух цветов: красный или синий. Докажите, что либо «красный», либо «синий» граф не является плоским.
Задача 27:
Семиугольник разбит на выпуклые пяти- и шестиугольники, причем так, что каждая его вершина является вершиной по крайней мере двух многоугольников разбиения. Докажите, что число пятиугольников разбиения не меньше 13.
Докажите что в плоском графе есть вершина степень которой не превосходит 5
В лаборатории Че проходит семинарам по доказательствам из Книги, как вошедшим в книгу Айгнера-Циглера, так и не вошедшим. Вчера Глеб Ненашев рассказал свою версию доказательства Ловаса теоремы Брукса, которого я раньше не знал.
Итак, докажем, что если в связном графе G степени всех вершин не превосходят d>2 и G не есть полный граф на d+1 вершине, то вершины G можно правильно покрасить в d цветов.
Начнем с нескольких простых наблюдений.
1) Если граф H нельзя покрасить в k цветов, то он содержит индуцированный подграф, в котором степени вершин не меньше k (то есть можно выкинуть из него несколько вершин так, что степени оставшихся будут не меньше k). Доказательство: если степень вершины v меньше k, то граф H-v также нельзя покрасить в k цветов (иначе покрасим его, а потом докрасим v). Удалим вершину v и продолжим процесс, в итоге останется подграф, в котором все степени не меньше k.
Перейдем к доказательству теоремы Брукса. Будем считать, что для графов с меньшим числом вершин, чем у G, утверждение теоремы Брукса выполняется, а для графа G нет. Тогда степени всех вершин графа G равны d, потому что согласно 1) в G есть подграф с таким свойством, а из-за связности он обязан совпадать с G.
Рассмотрим любую вершину p графа G, у нее найдутся два несмежных соседа u,v. Рассмотрим граф G/uv. По 2) его не покрасить в d цветов. Этот граф связен, и степени всех его вершин, кроме, возможно, вершины z, получаемой отождествлением u и v, не превосходят d. Кроме того, степень вершины p строго меньше, чем d. Следовательно, в нем по 1) найдется индуцированный подграф H, в котором степени всех вершин не меньше d. Этот подграф непременно содержит вершину z, потому что степени оставшихся и так были не больше d, а из-за связности мы должны были удалить какие-то ведущие в них ребра. Таким образом, в графе H есть вершина z и несколько вершин степени d, которые не смежны, таким образом, с вершинами вне H.
Попробуем теперь покрасить граф G+uv. Он состоит из графа H’, стягиванием ребра uv в котором служит граф H, и графа H
, состоящего из вершин u,v и вершин, не входящих в H’. Эти два графа имеют общее ребро uv, а их вершины, отличные от u и v, не смежны. Таким образом, если мы покрасим каждый из них d цветов, то склеивая эти раскраски по ребру uv (можно считать, что вершины u,v покрашены оба раза в белый и голубой цвета соответственно) получим раскраску графа G+uv. Заметим, что степени всех вершин графов H’, H
не превосходят d. В самом деле, для всех вершин, кроме u,v это очевидно, и проверить следует лишь что, например, вершина u, имеющая степень d+1 в графе G+uv, соединена не только с вершинами H’ или не только с вершинами H
. Первое ясно: вершина u соединена с вершиной p, лежащей в H
. Если же она соединена только с вершинами H
(оба имеют меньше вершин, чем G) выполняется утверждение теоремы Брукса, так что один из них должен быть полным графом на d+1 вершине. Это может быть только граф H
, поскольку в графе H’ вершины u,v не имеют общих соседей (такой общий сосед имел бы степень меньше d в графе H и потому попал бы в H
Докажите что в плоском графе есть вершина степень которой не превосходит 5
а) Какое наибольшее число рёбер может быть в 30-вершинном графе, в котором нет треугольников?
б) Какое наибольшее число рёбер может быть в 30-вершинном графе, в котором нет полного подграфа из четырёх вершин?
Подсказка
Выберите вершину наибольшей степени.
Решение
а) Оценка. Выберем вершину A наибольшей степени n и рассмотрим подграф G, образованный вершинами, куда ведут рёбра из A. Ясно, что в этом подграфе рёбер нет. Каждая вершина, не входящая в G имеет степень не больше n, а выходящие из них рёбра – это все рёбра исходного графа. Таким образом, общее число рёбер исходного графа не превосходит n(30 – n) ≤ 15².
Пример. Разобьём 30 вершин на две группы по 15 и проведём все рёбра, соединяющие вершины из разных групп. Получился граф без треугольников с 225 рёбрами.
б) Оценка. Выберем вершину A наибольшей степени n и рассмотрим подграф G, образованный вершинами, куда ведут рёбра из A. Ясно, что в этом подграфе нет треугольников, поэтому, как фактически доказано в а), число его рёбер не превосходит ( n /2)². Таким образом, общее число рёбер исходного графа не превосходит (n/2)² + n(30 – n) = 3 /4 n(40 – n) ≤ 3 /4·20² = 300.
Пример. Разобьём 30 вершин на три группы по 10 и проведём все рёбра, соединяющие вершины из разных групп. Получился граф без полных 4-подграфов с 300 рёбрами.
Ответ
Замечания
Эти задачи – частные случаи теоремы Турана (см. статью в Википедии).
Докажите что в плоском графе есть вершина степень которой не превосходит 5
Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.
Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.
Полный граф Линейка Звезда Кольцо 2-мерная решётка 3-мерная решётка Рис. 1.47. Примеры топологий многопроцессорных вычислительных систем 44 В.Н. Берцун. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ НА ГРАФАХ. Часть Задачи 1. Является ли в графе G ребро (AB) мостом A B 2. Найти простой цикл в графе. Является ли этот граф двудольным 7 3. Нарисуйте связный граф с семью вершинами и шестью ребрами.
4. Можно ли из полного графа с одиннадцатью вершинами удалить часть рёбер так, чтобы степень каждой вершины была равна семи 5. Какое наибольшее число ребер можно удалить, чтобы граф остался связным 6. При встрече n друзей обменялись рукопожатиями. Сколько было друзей, если рукопожатий было 28.
Глава 1. Основные понятия теории графов 7. Является ли граф двудольным 8. Сколько существует свободных деревьев с шестью вершинами 9. Есть ли среди свободных деревьев изоморфные 10. Составить дерево розыгрыша кубка по футболу среди 8 команд по олимпийской системе: без ничьих, проигравшая команда выбывает.
11. Изоморфны ли графы а б в г аб аб в 46 В.Н. Берцун. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ НА ГРАФАХ. Часть 12. В город прибыло три группы иностранных туристов Ti, i = 1, 2, 3, говорящих соответственно на английском, французском и итальянском языках. Туристическое бюро располагает пятью переводчиками Pi, i = 1, 2,…,5, владеющими соответственно языками:
английским, французским и итальянским, немецким и французским, китайским и итальянским, английским. Нарисовать двудольный граф распределения всех переводчиков по группам.
13. Имеется две урны, первая из которых содержит два белых и один черный шар, а вторая – один белый и два черных шара. Нарисовать дерево логических возможностей и определить число вариантов выбора шаров из урн.
14. Нарисовать дерево маршрутов движения, если в лабиринте на рис. 1.42 появится еще один тупик.
пища 2 1 3 5 8 15. Доказать, что каждое дерево является двудольным графом.
16. Для кодового дерева на рис. 1.41 записать таблицу кодирования букв и проверить ее оптимальность по частотной таблице букв русского языка [31].
17. Найти радиус, диаметр и центр графа 18. Нарисовать все помеченные графы с четырьмя вершинами.
19. Найти всевозможные цепи, соединяющие вершины графа А и В. Определить длину максимальной простой цепи.
A B Глава 1. Основные понятия теории графов 20. Нарисовать все возможные вырожденные бинарные деревья для n = 4.
21. Определить вершинную и реберную связность, диаметр и центр графов на рис. 1.47.
22. Доказать, что полный граф Kn имеет в точности nn–2 остовных деревьев.
23. Самая длинная простая цепь является диаметром графа. Доказать, что любые два диаметра имеют общую вершину.
24. Доказать, что простой граф на n вершинах не является двудольным, если он имеет более n2/4 ребер.
25. Доказать, что в дереве существуют хотя бы две висячие вершины.
26. Доказать, что при добавлении ребра между двумя любыми вершинами дерева в полученном графе образуется ровно один цикл.
27. При каких условиях a задаче Торричелли – Ферма точка Р находится внутри треугольника.
28. Записать матрицы смежности для графов C3, K3, K3,3.
29. Доказать, что диаметр графа не превосходит его удвоенного радиуса.
30. Сколько помеченных графов порождает простой цикл С5 Глава ПЛОСКИЕ И ПЛАНАРНЫЕ ГРАФЫ 2.1. Свойства плоского графа При изготовлении различных технических устройств (микросхем, транспортных сетей без пересечений и др.) важно знать, существует ли изоморфное представление соответствующего графа на плоскости (решение задачи), удовлетворяющее определенным технологическим требованиям.
Граф G называется плоским, если его можно нарисовать на плоскости так, чтобы никакие два его ребра не имели общих точек, кроме их общей вершины. Граф называется планарным, если он изоморфен плоскому графу (допускает плоскую укладку). На рис. 2.1 изображены планарный и плоские графы [3, 11].
Рис. 2.Очевидно, что плоскими графами являются: простые циклы, деревья, лес, географическая карта (без островных государств).
Гранью в плоском представлении графа G называется максимальное по включению множество точек плоскости, каждая пара которых может быть соединена жордановой кривой, не пересекающей ребра графа. Длина цикла, ограничивающего грань плоского графа, называется степенью грани. Две грани называются соседними, если Глава 2. Плоские и планарные графы они имеют хотя бы одно общее ребро.
В качестве грани можно рассматривать D C и часть плоскости, расположенную вне плоского графа. Такую плоскость называют бесконечной или внешней гранью. Грань может содержать дерево.
A B На рис. 2.2 изображена бесконечная грань. Примеры граней приведены на Рис. 2.рис. 2.3.
P D E F z A D H F x B E A C B C (A, D, C) – не грань, z – грань степени 4, (A, B, C, D, P) – (A, B, C) – грань x – грань степени 6 внешняя грань Рис. 2.Утверждение 2.1 (формула Эйлера). Если плоский связный граф имеет n вершин, m ребер и f граней, то n – m + f = 2. (1) Доказательство. Рассмотрим плоский связный граф. Преобразуем его в дерево, содержащее все его вершины. Для этого будем удалять те ребра, которые разомкнут простые циклы (см., например, рис. 2.4).
Тогда получится граф без перегородок и связный. Каждое удаление ребра уменьшает число граней на I, так как размыкается простой цикл либо из двух циклов образуется один. Таким образом, разРис. 2.ность m – f сохраняется. В полученном дереве пусть n1 – число вершин, m1 – число ребер, f1 – число граней.
Тогда m – f = m1 – f1 = m1 – 1, так как в дереве одна грань. По опреде50 В.Н. Берцун. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ НА ГРАФАХ. Часть лению в полученном дереве число вершин сохраняется, тогда n = n1.
Но дерево с n вершинами имеет n – 1 ребро. Тогда m1 = n – 1. Поэтому m – f = m1 – 1 = n – 2 или n – m + f = 2.
Ответ на вопрос о том, является ли данный граф плоским, очень часто не является очевидным и требует дополнительного анализа графа. Рассмотрим, например, задачу о трех домах и трех колодцах.
DE F A B C Рис. 2.Пусть имеется 3 дома и 3 колодца. От каждого дома к каждому колодцу идет тропинка. Можно ли проложить тропинки так, чтобы они не пересекались Решение задачи сводится к определению того, является ли полный двудольный граф K3,3 на рис. 2.5 плоским. Допустим, что он является плоским [34 – 37]. Для этого графа n = 6, m = 9 и из формулы (1) получим f = 2 + 9 – 6 = 5.
Отметим, что у двудольного графа K3,3 нет простых циклов длины 3, т.е. граница любой грани в плоском представлении содержит не менее четырех ребер. Тогда число граней f = f4 + f5 + f6 +. (2) где fi – число граней, ограниченных i ребрами. Но каждое ребро является границей двух граней (с учетом внешней грани), поэтому всего граней не больше 2m. С другой стороны, удвоенное число ребер можно вычислить через количество ребер в гранях 2m = 4f4 + 5f5 + 6f6 +. (3) Глава 2. Плоские и планарные графы С учетом (2), можно записать 4f = 4f4 + 4f5 + 4f6 +. (4) Тогда 4f 2m или 2f m. Но для m = 9, f = 5 получим, что 10 9.
Таким образом, граф K3,3 не плоский. Аналогичным образом можно показать, что полный граф с пятью вершинами K5, имеющий простые циклы длины 3, не плоский. Следовательно, имеется 2 типа не плоских графов: тип I – граф K3,3, тип II – граф K5.
По критерию Понтрягина – Куратовского необходимое и достаточное условие, при котором граф G является планарным, состоит в том, что граф не должен содержать подграфов типа I и типа II [15].
Для проверки планарности графа с n вершинами по этому критерию необходимо рассмотреть Сn5 графов с пятью вершинами и Сnграфов с шестью вершинами.
Рассмотрим плоский граф G на рис. 2.6. Если добавить к нему два ребра (штриховые линии), то он останется плоским.
Плоский граф называется максимально плоским если невозможно добавить к нему ни одного ребра так, чтобы новый граф был бы плоским. Каждая грань в максимально плоском графе имеет 3 вершины, поэтому максимально плоский граф называется триангулированным и Рис. 2.имеет ровно 3 внешних ребра.
Утверждение 2.2. Для любого планарного графа G существует плоская укладка, в которой все ребра – прямолинейные отрезки.
Доказательство. Будем рассматривать общий случай – максимально плоских графов. Для n 3) его непересекающимися диагоналями находится в последовательности Каталана [38] 1, 2, 5, 14, 42, 132, 429. где а1 = 1, аn = (2 n)! / [n! (n + 1)!], n > 1, Ln = аn–2.
Глава 2. Плоские и планарные графы Кэли установил, что числа Каталана перечисляют все плоские корневые кубические деревья, которые порождает триангуляция многоугольника его непересекающимися диагоналями.
Формула (1) получена Эйлером в 1758 г. для связного выпуклого многогранника в трехмерном пространстве с n вершинами, m ребрами и f гранями. Выпуклый многогранник можно представить на сфере, центр которой находится внутри его, таким образом, что никакие 2 ребра не пересекаются в точках, отличных от вершины. Стереографическая проекция такого графа является связным плоским графом [35]. Формула (1), отражающая фундаментальные свойства трехмерного пространства, не связана с расстоянием и углами, она стала основой для двух математических дисциплин – топологии и теории графов [34]. Известно, что существует только 5 правильных многогранников (пять Платоновых тел), плоские графы которых изображены на рис. 2.9.
Тетраэдр Куб Октаэдр Икосаэдр Додекаэдр (огонь) (земля) (воздух) (вода) (вселенная) Рис. 2.Если на ребра планарного (или непланарного) графа нанести произвольное число вершин степени 2, то полученный граф останется планарным (непланарным). Свойство планарности графа позволяет упростить, например, изготовление электронных схем по технологии напыления, создавать транспортные сети с минимальным числом пересечений.
2.2. Эйлеровы графы Можно ли нарисовать графы, изображенные на рис. 2.10, не отрывая карандаша от бумаги и не проходя по каждому ребру более одного раза Очевидно, что это можно сделать не для любого из этих графов [1 – 4].
54 В.Н. Берцун. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ НА ГРАФАХ. Часть Рис. 2.Эйлеровой цепью (в цепи ребро не встречается дважды) в графе называется цепь, содержащая все ребра графа. Эйлеровым циклом называется цикл, содержащий все ребра графа в точности один раз.
Граф, обладающий эйлеровым циклом, называется эйлеровым графом.
Утверждение 2.3. Если граф G обладает эйлеровым циклом, то он связный и все его вершины имеют четную степень.
Доказательство. Связность графа следует из определения эйлерова цикла. В эйлеровом цикле каждое ребро встречается только один раз, а каждая вершина встречается k 1 раз (или k + 1 раз, если это начальная и конечная вершины цикла, которые совпадают). Поэтому все вершины графа должны иметь четную степень 2k.
Утверждение 2.4. В графе G из всякого цикла можно выделить простой цикл.
Доказательство. Если длина цикла L = 1, то цикл есть петля и он прост. Пусть утверждение верно для всех графов с циклами длины до L – 1. Рассмотрим цикл длины L. Он либо простой, либо в нем есть вершины, повторяющиеся более одного раза. Цикл, существующий на таких вершинах, имеет длину меньше L и поэтому содержит простой цикл.
Утверждение 2.5. Если граф G связный и все его вершины имеют четную степень, то он обладает эйлеровым циклом.
Доказательство. Для петли, состоящей из одного ребра, эйлеров цикл существует. Допустим, что у связных графов с числом ребер m – 1 есть эйлеров цикл. У графа G с m ребрами четные степени вершин, поэтому он имеет хотя бы один простой цикл С. Если этот цикл содержит все ребра графа G, то С – эйлеров цикл. Если С не эйлеров цикл, то удалив из G все ребра цикла С, получим суграф G1.
В таком суграфе каждая компонента связности является либо изолиГлава 2. Плоские и планарные графы рованной вершиной, либо эйлеровым графом с четными степенями вершин и числом ребер меньшим m. В этом случае эйлеровым циклом связного графа G будет объединение простого цикла С с эйлеровыми циклами связных компонент подграфа G1.
Утверждение 2.6. Связный граф G обладает эйлеровой цепью с концами А и В тогда и только тогда, когда А и В единственные нечетные его вершины.
Доказательство. Необходимость. Пусть G имеет эйлерову цепь (А, В). Присоединим к этому графу новое ребро, соединяющее концы эйлеровой цепи. В полученном графе G1 степени всех вершин четные и, следовательно, существует эйлеров цикл. Тогда в графе G все вершины, кроме А и В, являются четными.
Достаточность. Пусть G связен и А, В – единственные его нечетные вершины. Соединив концы нечетных вершин, получим эйлеров граф G1, в котором эйлеров цикл содержит вершины А и В. Если в этом цикле исключить дополнительное ребро, то получим эйлерову цепь.
Если граф G связный и имеет 2k вершин нечетной степени, то в нем можно провести k различных цепей, содержащих все его ребра в совокупности ровно по одному разу [2, 36].
Рассмотрим пример. Пусть автобусная сеть имеет вид графа на рис. 2.11. Требуется найти минимальное число маршрутов, обеспечивающих проезд пассажиров из любого пункта в любой с пересадD С ками или без них. Каждый автобус А при этом должен двигаться по своему маршруту.
F Решение. Граф – не эйлеров, так Рис. 2.как имеет 4 нечетные вершины. Поэтому в этом графе существует два маршрута (две различные цепи), например, ADFC, DCAF. При решении прикладных задач (головоломок, лабиринтов и др.) возникает проблема построения замкнутого маршрута из некоторой вершины А, содержащего все ребра графа дважды. Такие задачи приводят к необходимости рассмотрения соответствующих ориентированных графов. Орграф является эйлеро56 В.Н. Берцун. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ НА ГРАФАХ. Часть вым, если в нем есть контур, проходящий по каждой дуге этого графа в точности один раз. Известно [1 – 3], что:
1) связный орграф – эйлеров, если в каждой его вершине полустепень захода равна полустепени исхода;
2) если граф G – связный, то можно построить цикличный маршрут, содержащий все его ребра в точности два раза, по одному разу в каждом из двух направлений.
Рассмотрим граф на рис. 2.12, a, в котором требуется найти замкнутый путь из вершины А, содержащий все ребра графа G, дважды по одному разу в каждом направлении.
А А аб Рис. 2.Для этой цели используем правило Тарри для связного графа [1].
Из произвольной вершины А начинаем движение вдоль любого ребра. Ребро, по которому впервые приходим в вершину, отмечаем, например, стрелкой с точкой. Ребро, по которому впервые попали в вершину, используем для выхода, если нет других возможностей.
Один из вариантов пути в этом случае представлен на рис. 2.12, б.
Утверждение 2.7. Почти нет эйлеровых графов [11].
Доказательство. Пусть G(n) – множество графов с n вершинами, Э(n) множество эйлеровых графов с n вершинами и мощностью Э(n). Если Э(n) – множество графов с n вершинами и четными степенями, тогда Э(n) Э (n) и | Э(n)| |Э(n)|.
В любом графе число вершин нечетной степени четно. Тогда любой граф из множества Э(n) можно получить из некоторого графа Глава 2. Плоские и планарные графы Gn–1 в множестве G(n – 1), если к нему добавить новую вершину и соединить ее со старыми вершинами нечетной степени. Поэтому |Э'(n)| |G(n – 1)|. C другой стороны, число графов с n вершинами определяется через количество ребер в полном графе |G(n)| = 2q, q = C(n, 2) = n(n – 1)/2.
Учитывая, что C(k,2)-C(k – 1, 2) = k – 1, получим |Э(n)| |Э'(n)| |G(n – 1)| = 2C(n–1, 2) = 2c(n, 2) – (n–1) = |G(n)|·2– (n–1).
Тогда = |Э(n)| / |G(n)| и 0 при n, 2n-т.е. почти нет эйлеровых графов.