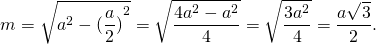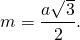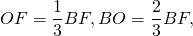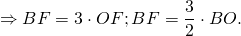Докажите что в равностороннем треугольнике все медианы равны
Медиана равностороннего треугольника
Какими свойствами обладает медиана равностороннего треугольника? Как выразить длину медианы через сторону треугольника? Через радиус вписанной и описанной окружностей?
(свойство медианы равностороннего треугольника)
В равностороннем треугольнике медиана, проведённая к любой стороне, является также его биссектрисой и высотой.

Проведём медиану BF.
Так как AB=BC, треугольник ABC — равнобедренный с основанием AC.
По свойству медианы равнобедренного треугольника, BF является также его биссектрисой и высотой.

так как AC=BC, треугольник ABC — равнобедренный с основанием AB, CD — его медиана, биссектриса и высота.
(свойство медиан равностороннего треугольника)
Все три медианы равностороннего треугольника равны между собой.

AK, BF, CD — его медианы.
Следовательно, треугольники ABK, BCF и CAK равны (по двум сторонам и углу между ними).
Из равенства треугольников следует равенство соответствующих сторон:
Из 1 и 2 теоремы следует, что все медианы, биссектрисы и высоты равностороннего треугольника равны между собой.
1) Выразим длину медианы равностороннего треугольника через его сторону.

Обозначим AB=a, BF=m, тогда AF=a/2.
Таким образом, формула медианы равностороннего треугольника по его стороне:
2) Выразим медиану равностороннего треугольника через радиусы вписанной и описанной окружностей.
Центр правильного треугольника является центром его вписанной и описанной окружностей.

Так как медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины, то BO:OF=2:1. Таким образом,
Отсюда медиана равностороннего треугольника через радиус вписанной окружности равна
Определение и свойства медианы равностороннего треугольника
В данной статье мы рассмотрим определение и свойства медианы равностороннего треугольника, а также разберем примеры решения задач для закрепления изложенного материала.
Определение медианы
Медиана – это отрезок, соединяющий вершину треугольника и середину противоположной стороны.
Треугольник называется равносторонним, если все его стороны равны (AB = BC = AC).
Свойства медианы равностороннего треугольника
Свойство 1
Любая медиана в равностороннем треугольнике одновременно является и высотой, и серединным перпендикуляром, и биссектрисой угла, из которого проведена.
Свойство 2
Все три медианы в равностороннем треугольнике равны между собой. Т.е. AF = BD = CE.
Свойство 3
Медианы в равностороннем треугольнике пресекаются в одной точке, которая делит их в отношении 2:1.
Свойство 4
Любая медиана равностороннего треугольника делит его на два равных по площади (равновеликих) прямоугольных треугольника. Т.е. S1 = S2.
Свойство 5
Равносторонний треугольник делится тремя медианами на шесть равновеликих прямоугольных треугольников. Т.е. S1 = S2 = S3 = S4 = S5 = S6.
Свойство 6
Точка пересечения медиан в равностороннем треугольнике является центром описанной вокруг и вписанной окружностей.
Свойство 7
Длину медианы равностороннего треугольника можно вычислить по формуле:
a – сторона треугольника.
Примеры задач
Задача 1
Вычислите длину медианы равностороннего треугольника, если известно, что его сторона равна 6 см.
Решение
Для нахождения требуемого значения применим формулу выше:
Задача 2
Самая большая сторона одного из треугольников, образованных в результате пересечения трех медиан в равностороннем треугольнике, равняется 8 см. Найдите длину стороны данного треугольника.
Решение
Нарисуем чертеж согласно условиям задачи.
Из Свойства 5 мы знаем, что в результате пересечения всех медиан образуются 6 прямоугольных треугольников.
BF равняется половине стороны BC (т.к. медиана делит сторону треугольника пополам), следовательно, BC ≈ 13,86 см.
Свойства равностороннего треугольника: теория и пример задачи
В данной статье мы рассмотрим определение и свойства равностороннего (правильного) треугольника. Также разберем пример решения задачи для закрепления теоретического материала.
Определение равностороннего треугольника
Равносторонним (или правильным) называется треугольник, в котором все стороны имеют одинаковую длину. Т.е. AB = BC = AC.
Примечание: правильный многоугольник – это выпуклый многоугольник, имеющий равные стороны и углы между ними.
Свойства равностороннего треугольника
Свойство 1
В равностороннем треугольнике все углы равны 60°. Т.е. α = β = γ = 60°.
Свойство 2
В равностороннем треугольнике высота, проведенная к любой из сторон, одновременно является биссектрисой угла, из которого она проведена, а также медианой и серединным перпендикуляром.
CD – медиана, высота и серединный перпендикуляр к стороне AB, а также биссектриса угла ACB.
Свойство 3
В равностороннем треугольнике биссектрисы, медианы, высоты и серединные перпендикуляры, проведенные ко всем сторонам, пересекаются в одной точке.
Свойство 4
Центры вписанной и описанной вокруг равностороннего треугольника окружностей совпадают и находятся на пересечении медиан, высот, биссектрис и серединных перпендикуляров.
Свойство 5
Радиус описанной вокруг равностороннего треугольника окружности в 2 раза больше радиуса вписанной окружности.
Свойство 6
В равностороннем треугольнике, зная длину стороны (условно примем ее за “a”), можно вычислить:
1. Высоту/медиану/биссектрису:
2. Радиус вписанной окружности:
3. Радиус описанной окружности:
4. Периметр:
5. Площадь:
Пример задачи
Дан равносторонний треугольник, сторона которого равна 7 см. Найдите радиус описанной вокруг и вписанной окружности, а также, высоту фигуры.
Решение
Применим формулы, приведеные выше, для нахождения неизвестных величин: