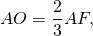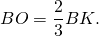Докажите что в равных треугольниках медианы

Длина медианы: \( \displaystyle <^<2>>=\frac <1>

В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.

Если медиана равна половине стороны, то треугольник прямоугольный и эта медиана проведена к гипотенузе.

Определение медианы треугольника

Это очень просто! Возьми треугольник.

Отметь на какой-нибудь его стороне середину \( \displaystyle M\).

И соедини с противоположной вершиной!

Получившийся отрезок \( \displaystyle BM\) и есть медиана.

Медиана треугольника – отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Медиана в прямоугольном треугольнике

Медиана равна половине гипотенузы прямоугольного треугольника!

Почему. При чём тут прямой угол?

Давай смотреть внимательно. Только не на треугольник, а на … прямоугольник.

Ты заметил, что наш треугольник \( \displaystyle ABC\) – ровно половина этого прямоугольника?

Проведём диагональ \( \displaystyle BD\):

Помнишь ли ты, что диагонали прямоугольника равны и делятся точкой пересечения пополам?

Но одна из диагоналей – \( \displaystyle AC\) – наша гипотенуза! Значит, точка пересечения диагоналей – середина гипотенузы \( \displaystyle \Delta ABC\).

Она называлась у нас \( \displaystyle M\).

Значит, половина второй диагонали – наша медиана \( \displaystyle BM\). Диагонали равны, их половинки, конечно же, тоже. Вот и получим \( \displaystyle BM=MA=MC\)

Медиана в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы.

Более того, так бывает только в прямоугольном треугольнике!

Если медиана равна половине стороны, то треугольник прямоугольный, и эта медиана проведена к гипотенузе.

Доказывать это утверждение мы не будем, а чтобы в него поверить, подумай сам: разве бывает какой-нибудь другой параллелограмм с равными диагоналями, кроме прямоугольника?

Нет, конечно! Ну вот, значит, и медиана может равняться половине стороны только в прямоугольном треугольнике.

Решение задач на свойства медианы в прямоугольном треугольнике

Давай посмотрим, как это свойство помогает решать задачи.

Задача №1:

В \( \displaystyle \Delta ABC\) стороны \( \displaystyle AC=5\); \( \displaystyle BC=12\). Из вершины \( \displaystyle C\) проведена медиана \( \displaystyle CN\).

Найти \( \displaystyle AB\), если \( \displaystyle AB=2CN\).

Сразу вспоминаем, это если \( \displaystyle CN=\frac<2>\), то \( \displaystyle \angle ACB=90<>^\circ \)!

Ура! Можно применить теорему Пифагора!

Видишь, как здорово? Если бы мы не знали, что медиана равна половине стороны только в прямоугольном треугольнике, мы никак не могли бы решить эту задачу. А теперь можем!

Применяем теорему Пифагора:

А в следующей задаче пусть у нас будет не одна, а целых три медианы! Как же они себя ведут?

Запомни очень важный факт:

Три медианы в треугольнике (любом!) пересекаются в одной точке и делятся этой точкой в отношении \( 2:1\), считая от вершины.

Сложно? Смотри на рисунок:

Медианы \( \displaystyle AM\), \( \displaystyle BN\) и \( \displaystyle CK\) пересекаются в одной точке.

Задача №2:

Решение:

\( \displaystyle \angle B=90<>^\circ \) – треугольник прямоугольный!

(Применили то, что медиана, проведённая к гипотенузе равна половине гипотенузы).

Найдём \( \displaystyle AC\) по теореме Пифагора:

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Теорема о медиане и площади треугольника

Медиана делит площадь треугольника пополам

Почему? А давай вспомним самую простую форму площади треугольника. \( S=\frac<1><2>a

И применим эту формулу аж два раза!

Посмотри, медиана \( \displaystyle BM\) разделила \( \displaystyle \triangle ABC\) на два треугольника: \( \displaystyle \triangle ABM\) и \( \displaystyle \triangle BMC\).

Но! Высота-то у них одна и та же – \( \displaystyle BH\)!

Только в \( \displaystyle \triangle ABM\) эта высота \( \displaystyle BH\) опускается на сторону \( \displaystyle AM\), а в \( \displaystyle \triangle BMC\) – на продолжение стороны \( \displaystyle CM\).

Удивительно, но вот бывает и так: треугольники разные, а высота – одна. И вот, теперь-то и применим два раза формулу

1) B \( \displaystyle \triangle ABM\):

«\( \displaystyle a\)» – это \( \displaystyle AM\) «\( \displaystyle h\)» – это \( \displaystyle BH\)

\( \displaystyle \Rightarrow <_<\triangle ABM>>=\frac <1> 2) B \( \displaystyle \triangle BMC\): «\( \displaystyle a\)» – это \( \displaystyle CM\) «\( \displaystyle h\)» – это опять \( \displaystyle BH\) \( \displaystyle \Rightarrow <_<\triangle BMC>>=\frac <1> Читать далее… Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз: Теорема о трех медианах треугольника Три медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении \( \displaystyle 2:1\ \), считая от вершины. Что бы это такое значило? Посмотри на рисунок. На самом деле утверждений в этой теореме целых два. Ты это заметил? 1. Медианы треугольника пересекаются в одной точке. 2. Точкой пересечения медианы делятся в отношении \( \displaystyle 2:1\ \), считая от вершины. Давай попробуем разгадать секрет этой теоремы, то есть доказать ее. Доказательство теоремы о трех медианах треугольника Сначала проведем не все три, а только две медианы. Они-то уж точно пересекутся, правда? Обозначим точку их пресечения буквой \( \displaystyle E\). Соединим точки \( \displaystyle N\) и \( \displaystyle K\). Что получилось? Конечно, \( \displaystyle NK\) – средняя линяя \( \displaystyle \triangle ABC\). Ты помнишь, что это значит? А теперь проведем ещё одну среднюю линию: отметим середину \( \displaystyle AE\) – поставим точку \( \displaystyle F\), отметим середину \( \displaystyle EC\) — поставим точку \( \displaystyle G\). Теперь \( \displaystyle FG\) – средняя линия \( \displaystyle \triangle AEC\). То есть: Что из этого следует? Посмотри теперь на четырехугольник \( \displaystyle NKGF\). У какого четырехугольника противоположные стороны (\( \displaystyle NK\) и \( \displaystyle FG\)) параллельны и равны? Конечно же, только у параллелограмма! Значит, \( \displaystyle NKGF\) – параллелограмм. Ну и что? А давай вспомним свойства параллелограмма. Например, что тебе известно про диагонали параллелограмма? Правильно, они делятся точкой пересечения пополам. Снова смотрим на рисунок. Читать далее… Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз: Формула длины медианы треугольника Как же найти длину медианы, если известны стороны? А ты уверен, что тебе это нужно? Откроем страшную тайну: эта формула не очень полезная. Но всё-таки мы её напишем, а доказывать не будем. Итак, \( \displaystyle <^<2>>=\frac <1> Бонусы: Вебинары из нашего курса подготовки к ЕГЭ по математике по треугольникам Лучше всего смотреть это видео с ручкой и тетрадкой в руках. То есть ставьте видео на паузу и решайте задачи самостоятельно. Помните, понимать и уметь решать — это два, совершенно разных навыка. Очень часто вы понимаете как решить задачу, но не можете это сделать. Или допускаете ошибки, или просто теряетесь и не можете найти ход решения. Как с этим справиться? Нужно решать много задач. Другого способа нет. Вы должны совершить свои ошибки, чтобы научиться их не допускать. ЕГЭ №6 Равнобедренный треугольник, произвольный треугольник В этом видео мы вспомним все свойства равнобедренных треугольников и научимся их применять в задачах из ЕГЭ. Очень часто все «проблемы» с решением задач на равнобедренный треугольник решаются построением высоты. Также мы научимся решать и «обычные» треугольники. ЕГЭ №6 Прямоугольный треугольник, теорема Пифагора, тригонометрия Большинство задач в планиметрии решается через прямоугольные треугольники. Как это так? Ведь далеко не в каждой задаче речь идёт о треугольниках вообще, не то что прямоугольных. Но на уроках этой темы мы убедимся, что это действительно так. Дело в том, что редкая сложная задача решается какой-то одной теоремой — почти всегда она разбивается на несколько задач поменьше. И в итоге мы имеем дело с треугольниками, зачастую — прямоугольными. В этом видео мы научимся решать задачи о прямоугольных треугольниках из ЕГЭ, выучим все необходимые теоремы и затронем основы тригонометрии. ЕГЭ №16. Подобие треугольников. Задачи н доказательство Это одна из самых сложных задачи в профильном ЕГЭ. Полные 3 балла за эту задачу получают менее 1% выпускников! Основная сложность – построение доказательств. Баллы здесь снимают за любой пропущенный шаг доказательства. Например, нам часто кажется очевидным, что треугольники на рисунке подобны и мы забываем указать, по какому признаку. И за это нам снимут баллы. В этом видео вы научитесь применять подобие треугольников для доказательств, указывать признаки подобия и доказывать каждое умозаключение. Вы научитесь правильно записывать решение задачи, сокращать записи чтобы не тратить время на выписывание всех своих мыслей или полных названий теорем. Вы научитесь также применять подобие треугольников не только для доказательств, а и для расчётных задач. Источник Если две медианы треугольника равны Если две медианы треугольника равны, то этот треугольник — равнобедренный. 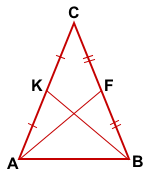Дано: ΔABC, 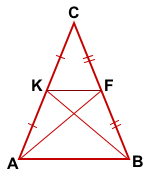Доказать: ΔABC — равнобедренный Так как AF и BK — медианы треугольника ABC, то точки F и K — середины отрезков BC и AC соответственно. Значит KF — средняя линия ΔABC. 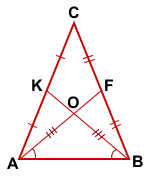Таким образом, AKFB — трапеция. Половины отрезков равны, значит равны и сами отрезки: AC=BC. Что и требовалось доказать. Пусть AF∩BK=O. Так как медианы треугольника точкой пересечения делятся в отношении 2 к 1, считая от вершины, то Так как AF=BK (по условию), то AO=BO. Следовательно, треугольник AOB — равнобедренный с основанием AB. Рассмотрим треугольники ABF и BAK. 2) сторона AB — общая, 3) ∠OAB=∠OBA (по доказанному). Значит треугольники ABF и BAK равны ( по 1 признаку). Из равенства треугольников следует равенство соответствующих углов:∠ABF=∠BAK. Отсюда треугольник ABC — равнобедренный с основанием AB (по признаку). Источник Популярная книга Круть доступна для чтения прямо сейчас на нашем сайте boochi.ru. Скачать книгу в формате FB2, TXT, PDF, EPUB бесплатно без регистрации. → Вам также понравится Для чего нужен рулевое управление 18.04.202220.04.2022 admin 0 Fernet branca что это за напиток 18.04.202218.04.2022 admin 0 Департамент 429 пао газпром чем занимается 18.04.202219.04.2022 admin 0 Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сохранить моё имя, email и адрес сайта в этом браузере для последующих моих комментариев.