Докажите что векторы противоположны

Общие сведения

Вектором называют направленный отрезок, который имеет начало и конец. Обозначают его либо большими буквами, либо маленькими, например, АБ или a. Над буквой ставится знак вектора — стрелка. Любой отрезок характеризуется длиной, которую называют модулем. Если начало и конец прямой совпадают, то такой вектор носит название нулевой и обозначается в виде точки. При этом его модуль будет равняться нулю.

Для равенства векторов необходимо выполнение двух условий:

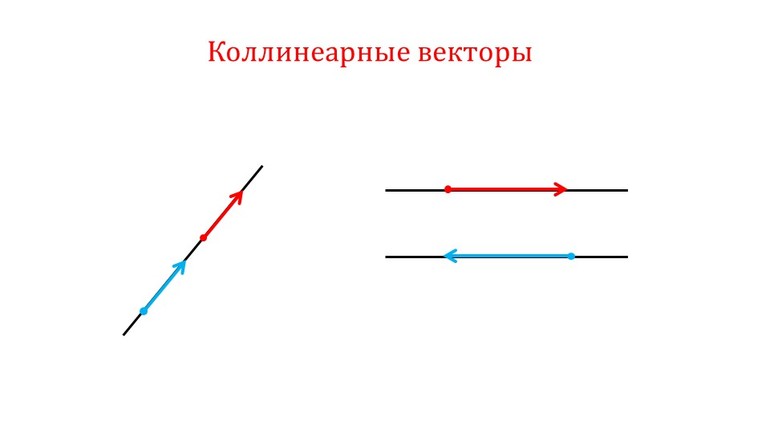
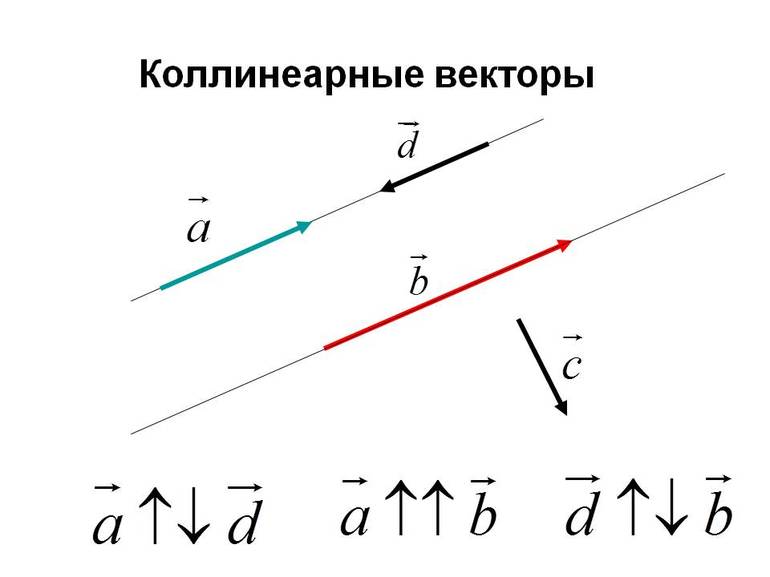
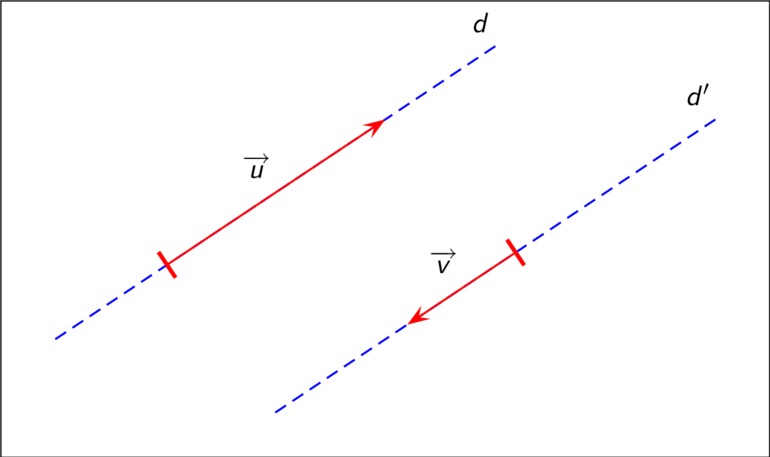
Равные вектора могут быть совмещены параллельным переносом, при этом начало и конец отрезков должны совпадать. Если ограниченные линии не являются равными, но лежат на параллельных прямых, то их называют коллинеарными, то есть, по определению коллинеарных векторов, их направление для определения признака не является важным.

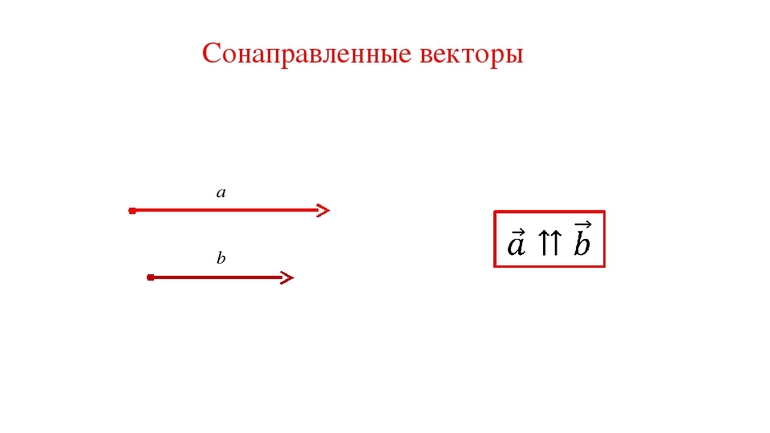
Коллинеарность является одним из признаков сонаправленности, но для выполнения последнего они должны ещё и совпадать по направлению. Наглядным понятием, объясняющим сонаправленность, является прямое движение транспорта или пешехода. Например, если рассматривать две траектории движения как векторы АБ и СД, лежащие на плоскости, при этом их лучи лежат в одной полуплоскости и перпендикулярны её границам, то их можно назвать сонаправленными.

Поэтому параллельные отрезки будут направлены в одну сторону лишь тогда, когда их лучи находятся по одну сторону от прямой, соединяющей их начала. При этом если векторы коллинеарны, но не сонаправлены, то они будут являться противоположными.

С векторами можно выполнять любые простейшие арифметические операции. При сложении используют правила параллелограмма и треугольника. Пусть есть два отрезка, имеющие общее начало. Для того чтобы найти их сумму, необходимо фигуру достроить до параллелограмма. Диагональ этой фигуры и будет искомой величиной. Когда же конец одного отрезка является началом другого, то, соединив свободные точки, можно получить треугольник. Новая прямая и будет являться вектором суммы. Следует отметить, что эти правила равнозначны друг другу. Вычитание отрезков находится аналогично.

Вектор можно и умножить на число, то есть длина отрезка увеличивается на значение множителя. Если в произведении стоит отрицательное число, то характеристика меняет направление.

Критерии коллинеарности

Теорема критерия коллинеарности представляет собой утверждение, которое сообщает, что если есть два не ортогональных отрезка, одинаковых по длине, a и b, то вектор a может быть выражен через формулу a || b = a = y * b. При этом y обозначает любое произвольное число. Есть и обратное утверждение: если вектор b умножить на число и получится отрезок a, то тогда a и b будут коллинеарными.

Эти два правила тождественны и называются критериями коллинеарности. Для их доказательства нужно знать правило арифметических действий с параллельными и перпендикулярными векторами, а также понимать основной базис. Заключается он в том, что если имеются три отрезка a, b и c, при этом верной является следующая комбинация a || b и a || c, то справедливо утверждать, что b || c.

Для того чтобы доказать свойство a || b = a = y * b, нужно воспользоваться определением коллинеарности. Из него следует, что если a || b, то отрезки могут быть сонаправлены или противоположно направлены. Таким образом, необходимо проверить утверждение для двух случаев:

Если предположения окажутся верными, то можно будет сделать вывод о справедливости записи для других случаев. То есть к любым параллельным отрезкам можно применить равенство a = u * b. Этот критерий занимает важное место в геометрии наряду со свойствами перпендикулярности (ортогональности) прямых.

Сонаправленные вектора

Пусть a и b однонаправленные. Введём число y, равное отношению a на b. Так как длина вектора может быть только положительной, то и y = a /b > 0. Состояние вектора, когда он нулевой, является частным случаем и его можно не рассматривать, так как при этом получится равенство 0 = 0. Если длину b умножить на число, то получится новый вектор. Пусть это будет отрезок c, то есть с = y * b. Учитывая свойство коллинеарности, можно утверждать, что между c и b останется параллельность.

По условию известно, что a || b. Исходя из транзитивности отрезков, можно заключить, что и c || b. Теперь необходимо установить их направление. Изначально a и b направлены в одну сторону. Ведённый множитель больше нуля. Это значит, что после умножения направление вектора не изменится, то есть c будет иметь то же направление что и b. Тогда получается, что a || b и c || b. Отсюда следует, что a || с.

Длина вектора c равняется |c| = |u| * |b|. Вместо u можно подставить a / b. В итоге получится |a| * |b| / |b| = |a|. Таким образом, два условия выполняются, и можно утверждать, что с = a. Получается, что для двух любых однонаправленных векторов будет выполняться правило a = u * b.

Противоположные отрезки

Использование онлайн-калькулятора

Решение простых заданий из школьного курса обычно не вызывает сложностей. Но на практике приходится сталкиваться со сложными выражениями. Для их вычисления нужно проявить усидчивость и при этом быть предельно внимательным. Кроме этого, расчёт занимает довольно много времени, а любая, казалось бы, незначительная оплошность, приведёт к неправильному решению.

Поэтому условие коллинеарности векторов удобно проверять на так называемых онлайн-калькуляторах. Это обычно мощные сервисы, основная деятельность которых заключается в предоставлении услуг по автоматизации вычислений. Среди них попадаются и сайты, умеющие вычислять и вектора.

Для того чтобы выполнить на них математические операции, необходимо иметь доступ к интернету и установленный веб-обозреватель. Всё, что требуется от пользователя, это просто зайти на сайт и выбрать раздел, связанный с операциями над векторами. Затем в предложенную форму вести условие задания и запустить расчёт нажатием одной кнопки.

Из множества онлайн-расчётчиков, доступных в секторе рунета, можно выделить следующие:

Все указанные сервисы предоставляют доступ к услугам бесплатно и без регистрации. Воспользовавшись онлайн-калькуляторами, даже слабо подготовленный пользователь научится самостоятельно определять коллинеарность. Такие расчётчики будут полезны и учащимся, и инженерам.

Источник

Докажите что векторы противоположны

Сформулируем ряд базовых определений.

Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или на параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы компланарны.

то есть модуль вектора равен корню квадратному из суммы квадратов его координат.

Обозначим углы между вектором и осями координат через α, β, γ соответственно. Косинусы этих углов называются для вектора направляющими, и для них выполняется соотношение: Верность данного равенства можно показать с помощью свойства проекции вектора на ось, которое будет рассмотрено в нижеследующем пункте 4.

Пусть в трехмерном пространстве заданы векторы своими координатами. Имеют место следующие операции над ними: линейные (сложение, вычитание, умножение на число и проектирование вектора на ось или другой вектор); не линейные – различные произведения векторов (скалярное, векторное, смешанное).

1. Сложение двух векторов производится покоординатно, то есть если

Геометрически два вектора складываются по двум правилам:

а) правило треугольника – результирующий вектор суммы двух векторов соединяет начало первого из них с концом второго при условии, что начало второго совпадает с концом первого вектора; для суммы векторов – результирующий вектор суммы соединяет начало первого из них с концом последнего вектора-слагаемого при условии, что начало последующего слагаемого совпадает с концом предыдущего;

б) правило параллелограмма (для двух векторов) – параллелограмм строится на векторах-слагаемых как на сторонах, приведенных к одному началу; диагональ параллелограмма исходящая из их общего начала, является суммой векторов.

Геометрически два вектора складываются по уже упомянутому правилу параллелограмма с учетом того, что разностью векторов является диагональ, соединяющая концы векторов, причем результирующий вектор направлен из конца вычитаемого в конец уменьшаемого вектора.

При λ>0 – вектор сонаправлен ; λ противоположно направлен ; | λ|> 1 – длина вектора увеличивается в λ раз; | λ| 1 – длина вектора уменьшается в λ раз.

4. Пусть в пространстве задана направленная прямая (ось l ), вектор задан координатами конца и начала. Обозначим проекции точек A и B на ось l соответственно через A ’ и B ’.

Рассмотрим некоторые основные свойства проекций:

1) проекция вектора на ось l равна произведению модуля вектора на косинус угла между вектором и осью, то есть ;

2.) проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол – прямой;

3) проекция суммы нескольких векторов на одну и ту же ось равна сумме проекций на эту ось.

Сформулируем определения и теоремы о произведениях векторов, представляющих нелинейные операции над векторами.

5. Скалярным произведением векторов и называется число (скаляр), равное произведению длин этих векторов на косинус угла φ между ними, то есть

Теорема 2.2. Необходимым и достаточным условием перпендикулярности двух векторов является равенство нулю их скалярного произведения

Следствие. Попарные скалярные произведения единичных орт равны нулю, то есть

Отсюда следует условие перпендикулярности ненулевых векторов и :

С помощью скалярного произведения векторов находят работу постоянной силы на прямолинейном участке пути.

Решение. Вычислим модули векторов и их скалярное произведение по теореме (2.3):

Пример 2.10. Затраты сырьевых и материальных ресурсов, используемых на производство одной тонны творога, заданы в таблице 2.2 (руб.).

Какова общая цена этих ресурсов, затрачиваемых на изготовление одной тонны творога?

Примечание. Действия с векторами, осуществленные в примере 2.10, можно выполнить на персональном компьютере. Для нахождения скалярного произведения векторов в MS Excel используют функцию СУММПРОИЗВ( ), где в качестве аргументов указываются адреса диапазонов элементов матриц, сумму произведений которых необходимо найти. В MathCAD скалярное произведение двух векторов выполняется при помощи соответствующего оператора панели инструментов Matrix

Решение. Находим вектор перемещения, вычитая из координат его конца координаты начала

Угол φ между и находим по формуле (2.29), то есть

– перпендикулярен векторам и ;

– векторы образуют правую тройку (рис. 2.15).

Примечание. Определитель (2.25) раскладывается по свойству 7 определителей

Следствие 1. Необходимым и достаточным условием коллинеарности двух векторов является пропорциональность их соответствующих координат

Следствие 2. Векторные произведения единичных орт равны

Следствие 3. Векторный квадрат любого вектора равен нулю

Также с помощью векторного произведения можно определить момент силы относительно точки и линейную скорость вращения.

— перпендикулярен плоскости, проходящей через точки O , A , B ;

Следовательно, момент силы относительно точки O представляет собой векторное произведение

Решение. Найдем векторное произведение заданных векторов по формуле (2.32).

Теорема 2.6. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения

Теорема 2.7. Если три вектора заданы своими координатами, то их смешанное произведение представляет собой определитель третьего порядка, составленный из координат векторов- сомножителей соответственно, то есть

Объем треугольной пирамиды, построенной на этих же векторах, равен

Решение. Найдем координаты векторов

По формуле (2.36) объем пирамиды, построенной на векторах равен (единиц объема)

Рассмотрим очень важный вопрос о разложении вектора по базису. Приведем следующие определения.

получим выражение вектора через остальные векторы

Линейно независимыми называют векторы, если равенство (2.37) выполняется только тогда, когда все

Базисом n – мерного пространства E_n называют любую совокупность линейно независимых векторов n – мерного пространства.

Произвольный вектор n – мерного пространства можно представить в виде линейной комбинации векторов базиса таким образом:

Линейное пространство называется конечномерным и имеет размерность n , если в этом пространстве существует система из n линейно независимых векторов (базис) такая, что каждое ее расширение приводит к линейной зависимости системы.

Источник

Геометрия

Лучшие условия по продуктам Тинькофф по этой ссылке

Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера

. 500 руб. на счет при заказе сим-карты по этой ссылке

Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке

План урока:

Понятие вектора в пространстве

Напомним, что в курсе планиметрии мы уже подробно изучали вектора и действия с ними. При этом предполагалось, что все вектора располагаются в одной плоскости. Однако можно расширить понятие вектора так, чтобы они использовались и в стереометрии. В таком случае вектора уже могут располагаться в различных плоскостях.

Начнем с определения вектора:

Конец вектора обозначают с помощью стрелки. Посмотрим на рисунок:

Здесь показаны сразу три вектора:

У вектора АВ начало находится в точке А, а конец – в точке В. Аналогично у вектора С D точка С – это начало, а D – это конец. В обоих случаях начало и конец – это различные точки, поэтому АВ и CD именуют ненулевыми векторами. Если же начало и конец находятся в одной точке, например в Т, то получается нулевой вектор ТТ. Всякую точку в пространстве можно рассматривать как нулевой вектор:

Длина вектора АВ – это длина соответствующего ему отрезка АВ. Для обозначения длины используют квадратные скобки:

Естественно, что нулевой вектор имеет нулевую длину.

Далее напомним понятие коллинеарных векторов:

Коллинеарные вектора могут быть либо сонаправленными, либо противоположно направленными. Сонаправленные вектора находятся на сонаправленных лучах. Рассмотрим пример с кубом:

Здесь показаны вектора AD и ВС. Они сонаправленные, этот факт записывается так:

Вектора AD и FE располагаются на скрещивающихся прямых, поэтому они не коллинеарны. Их нельзя считать ни сонаправленными, ни противоположно направленными.

Сонаправленные вектора, имеющие одинаковую длину, именуются равными.

Рассмотрим несколько простейших задач.

Задание. В прямоугольном параллелепипеде АВС DA ₁ B ₁ C ₁ D ₁ известны три его измерения:

Решение. Для нахождения длин этих векторов достаточно вычислить длину отрезков СВ, DB и DB ₁. Проще всего вычислить СВ, ведь отрезки СВ и AD одинаковы как стороны прямоугольника АВ CD :

Вектора АМ и МВ также коллинеарны и имеют одинаковую длину, но они противоположно направлены, а потому равными не являются.

Операции над векторами

Такой метод сложения векторов именуется правилом треугольника. Если нужно сложить больше двух векторов, то используют правило многоугольника. В этом случае необходимо каждый следующий вектор откладывать от конца предыдущего. При этом в стереометрии вектора могут располагаться в различных плоскостях, то есть они на самом деле многоугольник не образуют:

Напомним, что в планиметрии существовали так называемые противоположные вектора. Есть они и в стереометрии:

Главное свойство противоположных векторов заключается в том, что в сумме они дают нулевой вектор:

Заметим, что для получения противоположного вектора достаточно поменять его начало и конец, то есть в записи вектора обозначающие его буквы надо просто записать в обратном порядке:

1) b и a будут коллинеарными векторами;

Если k – положительное число, то вектора a и b будут сонаправленными. Если же k a и b будут направлены противоположно.

Задание. Дан параллелепипед АВС D А₁В₁С₁ D ₁. Постройте вектор, который будет являться суммой векторов:

Решение. В каждом случае необходимо заменить один из векторов в сумме на другой равный ему вектор так, чтобы можно было применить правило треугольника.

В задании а) вектор А₁ D ₁ заменить равным ему вектором ВС. В итоге получится вектор АС.

В задании б) заменяем А D ₁ на вектор ВС₁. Также можно было бы заменить АВ на D ₁ C ₁. В обоих случаях сумма окажется равной АС₁.

В задании в) удобно DA заменить на C ₁В₁, тогда искомой суммой будет вектор С₁В.

В задании г) производим замену DD ₁ на равный ему вектор BB ₁. Тогда сумма DB и BB ₁– это вектор DB ₁.

В задании д) необходимо заменить ВС на В₁С₁. В итоге получаем вектор DC :

Решение. В случае а) сначала запишем очевидное равенство векторов, вытекающее из правило многоугольника:

Обратите внимание, что здесь у каждого следующего слагаемого начальная точка совпадает с конечной точкой предыдущего слагаемого, поэтому равенство и справедливо:

Однако по условию а) нам надо использовать другие вектора для выражения АВ. Мы можем просто заменить вектора CD и DB на противоположные:

Теперь можно составить и выражение для АВ:

Аналогично решаем и задания б) и в):

Задание. Р – вершина правильной шестиугольной пирамиды. Докажите, что сумма векторов, совпадающих с ребрами этой пирамиды и начинающихся в точке Р, в точности равна сумме векторов, которые совпадают с апофемами пирамиды и при этом также начинаются в точке Р.

Решение. Обозначим вершины буквами А₁, А₂, … А₆, а середины сторон шестиугольника, лежащего в основании, буквами Н₁, Н₂, … Н₆, как это показано на рисунке:

Нам надо показать, что сумма красных векторов равна сумме черных векторов:

Теперь отдельно построим правильный шестиугольник, лежащий, в основании пирамиды:

Ясно, что вектора, образованные сторонами этого шестиугольника, в сумме дают нулевой вектор (по правилу многоугольника):

Так как точки Н₁, Н₂, … Н₆ – середины сторона, то вектора Н₆А₆, Н₅А₅,…Н₁А₁ будут вдвое короче векторов А₁А₆, А₆А₅, … А₂А₁. При этом они находятся на одних прямых, поэтому справедливы равенства:

Таким образом нам удалось из верного равенства (3) доказать (2), из которого в свою очередь следует справедливость и (1), ч. т. д.

Задание. Упростите выражения:

Решение. Здесь надо просто применить законы сложения и умножения векторов, как это делалось и в курсе планиметрии. Сначала раскрываем скобки, а потом приводим подобные слагаемые:

Компланарные векторы

Если мы отложим несколько векторов от одной точки, то они либо будут находиться в одной плос-ти, либо располагаться в различных плос-тях. В первом случае их именуют компланарными векторами, а во втором – некомпланарными.

Любые два вектора будут компланарны, ведь при их откладывании от одной точки мы получаем две пересекающихся прямых, а через них всегда можно провести плос-ть. Однако если векторов более двух, то они могут быть как компланарны, так и некомпланарны.

Рассмотрим для примера параллелепипед:

Здесь вектора АС, АВ и АD компланарны, так как все они принадлежат одной грани (то есть плос-ти) АВСD. А вектора АВ, АD и АА₁ некомпланарны, ведь через них нельзя провести одну плос-ть.

Очевидно, что если из трех векторов любые два коллинеарны, то вся тройка векторов компланарна, ведь при откладывании векторов от одной точки коллинеарные вектора окажутся на одной прямой.

Существует признак компланарности векторов:

Напомним, что подразумевается под разложением вектора. Пусть есть вектора а, b и c. Если существуют такие числах и y, при которых выполняется равенство

то говорят, что вектор с разложен по векторам а и b, причем числа xи y называются коэффициентами разложения.

Докажем сформулированный признак. Пусть есть три вектора а, b и c, а также числа xи y, такие, что

Эти вектора находятся в одной плос-ти ОАВ. Теперь от той же точки О отложим вектора ха и уb, концы которых окажутся в точках А₁ и В₁:

Естественно, что вектора ОА₁ и ОВ₁ также окажутся в плос-ти ОАВ. Тогда и их сумма будет принадлежать этой плос-ти, а эта сумма как раз и есть вектор с:

В итоге получили, что а, b и с располагаются в одной плос-ти, то есть они компланарны.

Справедливо и обратное утверждение. Если вектора а, b и с компланарны, но а и b неколлинеарны, то вектор с можно разложить на вектора a и b. Это утверждение прямо следует из изученной в 9 классе теоремы о разложении векторов. Важно отметить, что коэффициенты такого разложения определяются однозначно.

Для сложения тройки некомпланарных векторов можно применить так называемое правило параллелепипеда. Если есть три некомпланарных вектора, то можно отложить их от одной точки О и далее построить параллелепипед, в котором эти вектора будут ребрами. Тогда диагональ этого параллелепипеда, выходящая из точки О, и будет суммой этих трех векторов:

Разложение вектора на некомпланарные вектора

Иногда вектор можно разложить не на два, а на три вектора. Выглядит такое разложение так:

Для доказательства рассмотрим три некомпланарных вектора а, bи c, а также произвольный вектор р. Отложим их от одной точки О. Обозначим концы этих векторов большими буквами А, В, С и Р:

Через ОВ и ОА можно провести некоторую плос-ть α. Точка С ей принадлежать не может, ведь ОА, ОВ и ОС – некомпланарные вектора. Проведем через Р прямую, параллельную ОС. Так как ОС пересекает α, то и параллельная ей прямая также пересечет α в некоторой точке Р₁. (Примечание. Если Р принадлежит α, то точки Р и Р₁ совпадут, то есть вектор Р₁Р будет нулевым).

Далее через точку Р₁ в плос-ти α проведем прямую, параллельную ОВ, которая пересечет ОА в точке Р₂. Заметим, что вектор ОР₂ находится на той же прямой, что и вектор ОА, то есть они коллинеарны, поэтому существует такое число х, что

Итак, мы показали, что у произвольного вектора p есть разложение на заранее заданные некомпланарные вектора. Осталось показать, что существует только одно такое разложение. Докажем это методом от противного. Пусть есть второе разложение с другими коэффициентами х₁, у₁ и z₁:

В правой части находятся три вектора, которые в сумме нулевой вектор. По правилу сложения векторов это означает, что эти вектора образуют треугольник, то есть находятся в одной плос-ти:

Значит, они компланарны. Тогда компланарны и вектора a, b и с, что противоречит условию теоремы. Значит, второго разложения р на заданные некомпланарные векторы не существует, ч. т. д.

Задание. АВСD и А₁В₁С₁D₁ – параллелограммы, располагающиеся в разных плос-тях. Докажите, что тройка векторов ВВ₁, СС₁ и DD₁ компланарна.

Решение. Сначала построим рисунок по условию задачи:

Для доказательства используем признак компланарности векторов. Для этого надо один из векторов, отмеченных на рисунке красным, разложить на два других вектора.

В результате нам удалось разложить СС₁ на вектора BB₁ и CC₁. Значит, эти три вектора коллинеарны.

Задание. В параллелепипеде АВСDA₁B₁C₁D₁ запишите разложение вектора BD₁ по векторам ВА, ВС и ВВ₁.

Решение. Сначала представим вектор BD₁ как сумму трех векторов:

Теперь заметим, что вектора С₁D₁ и ВА соответствуют ребрам параллелепипеда. Эти ребра одинаковы по длине и параллельны, поэтому и вектора будут равными. Аналогично равны вектора СС₁ и ВВ₁:

Задание. АВСD – тетраэдр, а точка К делит его ребро ВС пополам. Разложите вектор DK по векторам DA, AB и AC.

Решение. Сначала запишем очевидное выражение для вектора DK:

Задание. В точке М пересекаются медианы треугольника АВС, а О – произвольная точка в пространстве. Разложите вектор ОМ по векторам ОА, ОВ и ОС.

Решение. Медиану, проходящую через точку А, мы обозначим как АА₁, то есть А₁ – это середина отрезка ВС. Также буквой К обозначим середину ОВ:

Сначала разложим вектор ОА₁ на ОВ и ОС. Это можно сделать, ведь они компланарны. КА₁ – это средняя линия ∆ОСВ, поэтому КА₁||ОС и КА₁ вдвое короче ОС. Это значит, что

Так как АА₁ – медиана, то точка М делит ее в отношении 2:1. Отсюда вытекает следующее соотношение:

Только что решенная задача может быть использована и при решении другого, более сложного задания.

Задание. Докажите, что в параллелепипеде АВСDА₁В₁С₁D₁ плос-ти А₁ВD и СB₁D₁ делят диагональ АС₁ на три равных отрезка.

Решение. Обозначим точкой K точку пересечения медиан ∆А₁ВD. Тогда по формуле, выведенной в предыдущей задаче, мы получаем, что

Это соотношение означает, что вектора АК и АС₁ коллинеарны, поэтому они располагаются на одной прямой (они не могут находиться на параллельных прямых, ведь у них есть общая точка А). Значит, точка K принадлежит диагонали АС₁, и отрезок АК втрое короче диагонали.

Аналогично можно показать, что и

Из этого также вытекает, что М принадлежит диагонали АС₁, и МС₁ втрое короче АС₁. Значит, точки М и К делят диагональ на три равных отрезка, ч. т. д.

Сегодня мы расширили понятие векторов и научились их применять не только в планиметрических, но и в стереометрических задачах. При сохраняются все правила, по которым выполняются действия над векторами. Также в стереометрии появляется новое понятие компланарных и некомпланарых векторов.

Источник