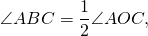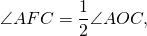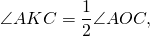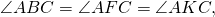Докажите что вписанные углы опирающиеся на 1 и ту же дугу равны
Теорема о вписанном угле
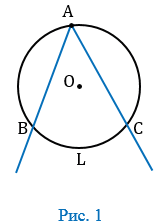
На рисунке 1 угол ВАС вписанный, дуга ВLС расположена внутри этого угла. В таком случае говорят, что вписанный угол АВС опирается на дугу ВLC.
Теорема
| Вписанный угол измеряется половиной дуги, на которую он опирается. |
Доказательство
Доказать: 
АВС = 
АС.
Доказательство:
Луч ВО совпадает с одной из сторон угла АВС.
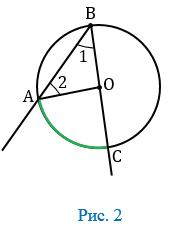
Пусть ВО совпадает с ВС (Рис. 2).
В данном случае дуга АС меньше полуокружности, следовательно, АОС =АС (т.к. АОС — центральный угол, причем он меньше полуокружности, поэтому градусная мера центрального угла равна градусной мере дуги, на которую он опирается).
Луч ВО делит угол АВС на два угла.
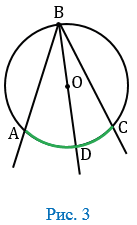
В данном случае луч ВО пересекает дугу АС в некоторой точке D (Рис. 3).
Точка D разделят дугу АС на две дуги: АD и DС, поэтому АС = АD + DС.
Луч ВD разделяет угол АВС на два угла, поэтому АВС = АВD + DВС.
По доказанному в 1 случае АВD = АD и DВС = DС. Складывая эти равенства, получаем: АВD + DВС = АD + DС или АВD + DВС = (АD + DС). Следовательно, АВС = АС.
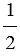
Луч ВО не делит угол АВС на два угла и не совпадает со стороной этого угла.
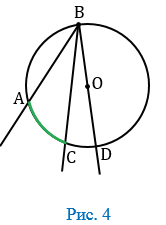
В данном случае луч ВС пересекает дугу АD в точке С (Рис. 4).
Луч ВС разделяет угол АВD на два угла, поэтому АВD = АВC + CВD, откуда АВC = АВD — CВD.
Теорема доказана.
Следствия из теоремы о вписанном угле
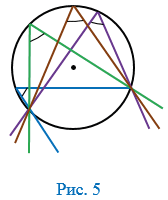
| 1. Вписанные углы, опирающиеся на одну и ту же дугу, равны (Рис. 5). |
Теорема
| Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. |
Доказательство
Доказать: АЕ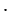
ВЕ = СЕDЕ.
Доказательство:
В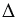 
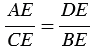
АDЕ и СВЕ: 1 = 2, т.к. они вписанные и опираются на одну и ту же дугу ВD (смотри следствие 1 из теоремы о вписанном угле), 3 = 4 как вертикальные углы, следовательно, треугольники АDЕ и СВЕ подобны (по 1 признаку подобия треугольников). В подобных треугольниках сходственные стороны пропорциональны, поэтому 
, откуда АЕВЕ = СЕDЕ. Теорема доказана.
Теорема
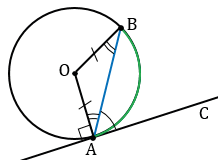
| Угол между касательной и хордой, проведенной в точку касания, равен половине дуги, стягиваемой этой хордой. |
Доказательство
Доказать: ВАС = АВ.
Доказательство:
Поделись с друзьями в социальных сетях:
Вписанные углы, опирающиеся на одну дугу
Вписанные углы, опирающихся на одну дугу (или на одну хорду), обладают полезным свойством, вытекающим из теоремы о вписанном угле.
Следствие из теоремы о вписанном угле.
Вписанные углы, опирающиеся на одну дугу (или на одну хорду), равны.
вписанный угол равен половине соответствующего ему центрального угла.
Отсюда, любой вписанный угол, опирающийся на дугу AC, равен половине центрального угла AOC (или половине дуги AC).
Что и требовалось доказать.
Это свойство вписанных углов очень часто используется при решении задач. Позже мы рассмотрим несколько таких задач.