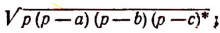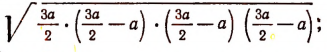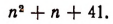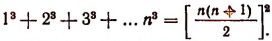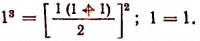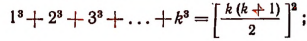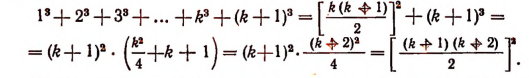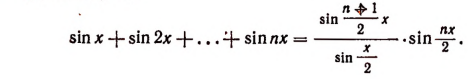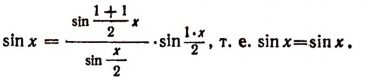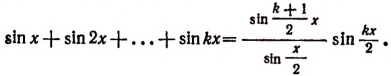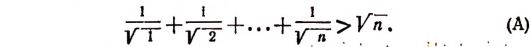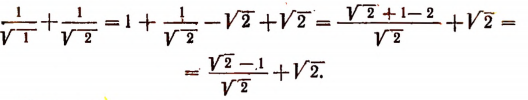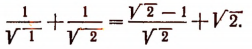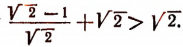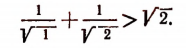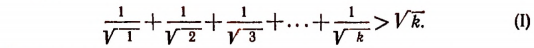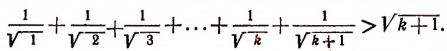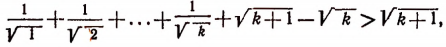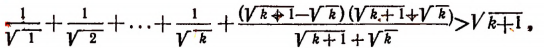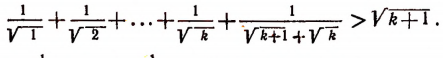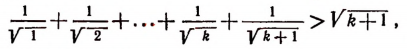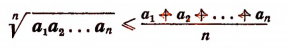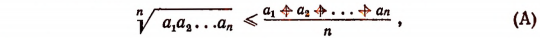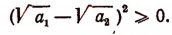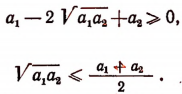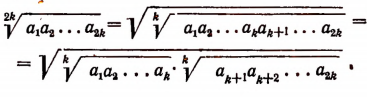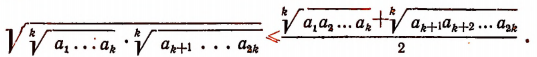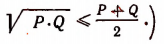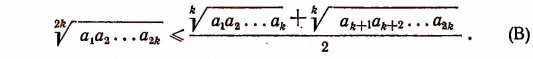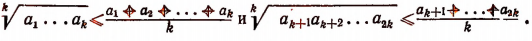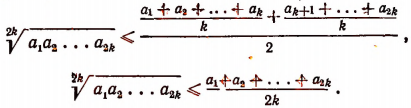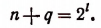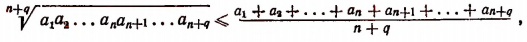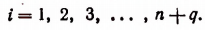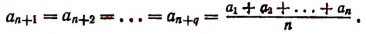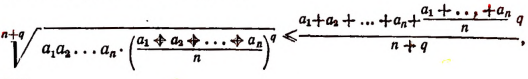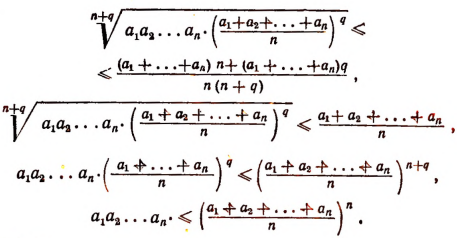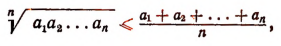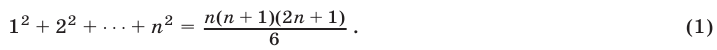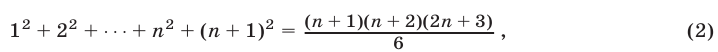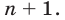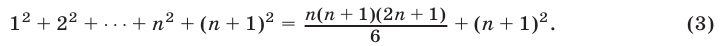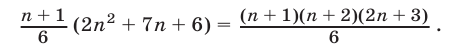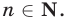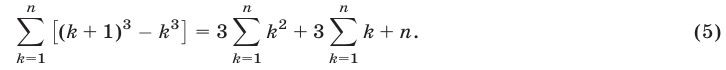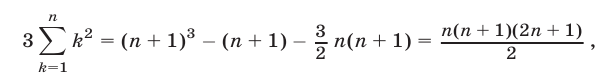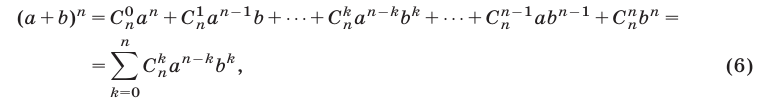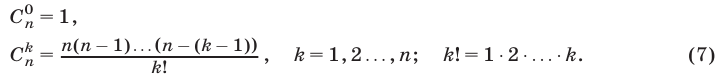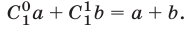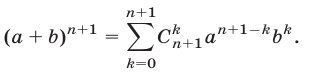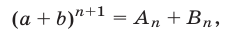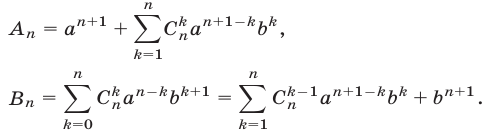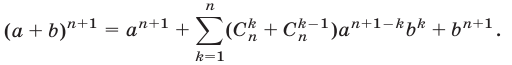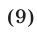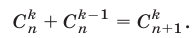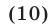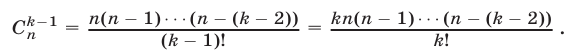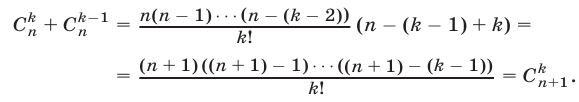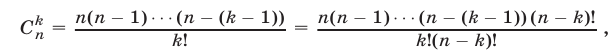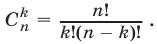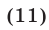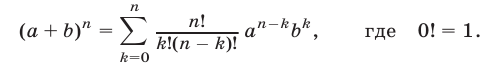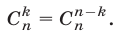Докажите методом математической индукции что общий
Метод математической индукции для чайников
Метод полного перебора конечного числа случаев, исчерпывающих все возможности, называется полной индукцией. Этот метод имеет крайне ограниченную область применения в математике, так как обычно математические утверждения касаются бесконечного множества объектов (например, натуральных чисел, простых чисел, квадратов и т.п.) и перебрать их невозможно.
Основы метода математической индукции
Доказательство с помощью метода математической индукции проводится в два этапа:
Метод математической индукции применяется в разных типах задач:
Ниже вы найдете примеры решения задач, иллюстрирующие применение метода математической индукции, а также ссылки на полезные сайты и учебник и небольшой видеоурок по ММИ.
Математическая индукция: задачи и решения
Доказательство кратности и делимости
$$a_n = 2n^3+3n^2+7n, \quad b=6.$$
Доказательство равенств и неравенств
Задача 5. Доказать равенство
Задача 6. Доказать методом математической индукции:
Задача 7. Доказать неравенство:
Задача 8. Доказать утверждение методом математической индукции:
Задача 9. Доказать неравенство:
Вычисление сумм
Задача 11. Доказать методом математической индукции:
Задача 12. Найдите сумму
Заказать решение
Полезные ссылки о ММИ
Кратенький видеоурок о ММИ
Метод математической индукции.
В этой статье сначала остановимся на основных понятиях, далее рассмотрим сам метод математической индукции и разберем примеры его применения при доказательстве равенств и неравенств.
Навигация по странице.
Индукция и дедукция.
Индукцией называют переход от частных утверждений к общим. Напротив, переход от общих утверждений к частным называется дедукцией.
Пример частного утверждения: 254 делится на 2 без остатка.
Из этого частного утверждения можно сформулировать массу более общих утверждений, причем как истинных так и ложных. К примеру, более общее утверждение, что все целые числа, оканчивающиеся четверкой, делятся на 2 без остатка, является истинным, а утверждение, что все трехзначные числа делятся на 2 без остатка, является ложным.
Таким образом, индукция позволяет получить множество общих утверждений на основе известных или очевидных фактов. А метод математической индукции призван определить справедливость полученных утверждений.
В качестве примера, рассмотрим числовую последовательность: 
Исходя из этого факта, по индукции можно утверждать, что 
Доказательство этой формулы приведем чуть ниже.
Метод математической индукции.
В основе метода математической индукции лежит принцип математической индукции.
То есть, доказательство по методу математической индукции проводится в три этапа:
Примеры доказательств уравнений и неравенств методом математической индукции.
Вернемся к предыдущему примеру и докажем формулу 
Метод математической индукции предполагает доказательство в три пункта.
Докажем, что 
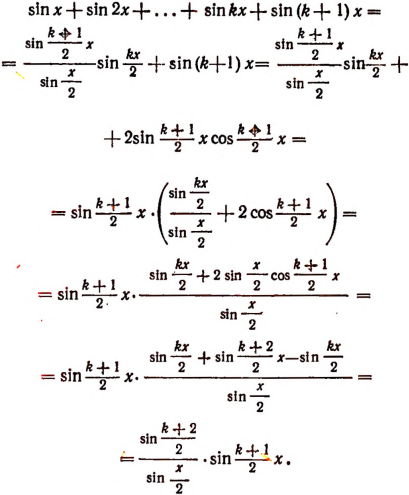
Сумма k+1 первых членов последовательности представляется как сумма первых k членов исходной числовой последовательности и k+1 ого члена:
Так как 
Осталось привести дроби к общему знаменателю, привести подобные слагаемые, воспользоваться формулой сокращенного умножения квадрат суммы и произвести сокращение:
Следовательно, доказано равенство третьего пункта.
Таким образом, выполнены все три шага метода математической индукции и тем самым доказано наше предположение о формуле 
Давайте рассмотрим тригонометрическую задачу.
Докажите тождество 
Так как по формуле из тригонометрии

то
Доказательство равенства из третьего пункта завершено, следовательно, исходное тождество доказано методом математической индукции.
Формула бинома Ньютона может быть доказана методом математической индукции.
Пример доказательства неравенства методом математической индукции можете посмотреть в разделе метод наименьших квадратов при выводе формул для нахождения коэффициентов аппроксимации.
Метод математической индукции
В первом пункте мы разберем основные понятия, потом рассмотрим основы самого метода, а затем расскажем, как с его помощью доказывать равенства и неравенства.
Понятия индукции и дедукции
Для начала рассмотрим, что такое вообще индукция и дедукция.
Индукция – это переход от частного к общему, а дедукция наоборот – от общего к частному.
В целом можно сказать, что с помощью индуктивных рассуждений можно получить множество выводов из одного известного или очевидного рассуждения. Математическая индукция позволяет нам определить, насколько справедливы эти выводы.
В чем заключается метод математической индукции
В основе этого метода лежит одноименный принцип. Он формулируется так:
Применение метода математической индукции осуществляется в 3 этапа:
Как применять метод математической индукции при решении неравенств и уравнений
Возьмем пример, о котором мы говорили ранее.
Решение
Как мы уже знаем, для применения метода математической индукции надо выполнить три последовательных действия.
Мы можем представить k + 1 в качестве суммы первых членов исходной последовательности и k + 1 :
S k + 1 = S k + 1 k + 1 ( k + 2 )
Теперь выполняем нужные преобразования. Нам потребуется выполнить приведение дроби к общему знаменателю, приведение подобных слагаемых, применить формулу сокращенного умножения и сократить то, что получилось:
S k + 1 = S k + 1 k + 1 ( k + 2 ) = k k + 1 + 1 k + 1 ( k + 2 ) = = k ( k + 2 ) + 1 k + 1 ( k + 2 ) = k 2 + 2 k + 1 k + 1 ( k + 2 ) = ( k + 1 ) 2 k + 1 ( k + 2 ) = k + 1 k + 2
Таким образом, мы доказали равенство в третьем пункте, выполнив все три шага метода математической индукции.
Ответ: предположение о формуле S n = n n + 1 является верным.
Возьмем более сложную задачу с тригонометрическими функциями.
Решение
cos 2 1 = cos 2 α sin 2 1 + 1 α 2 1 sin 2 α = sin 4 α 2 sin 2 α = 2 sin 2 α · cos 2 α 2 sin 2 α = cos 2 α
Согласно тригонометрической формуле,
Ответ: На этом тождество можно считать доказанным. Мы успешно применили для этого метод математической индукции. Точно так же мы можем доказать справедливость формулы бинома Ньютона.
Пример решения задачи на доказательство неравенства с применением этого метода мы привели в статье о методе наименьших квадратов. Прочтите тот пункт, в котором выводятся формулы для нахождения коэффициентов аппроксимации.
Математическая индукция в математике с примерами решения и образцами выполнения
Дедукцией называется переход от общего утверждения к частному. Приведем пример.
Площадь всякого треугольника равна
это утверждение общее.
От этого общего утверждения можно сделать переход к частному утверждению, например такому:
площадь равностороннего треугольника равна
т. е. равна 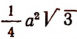
Дедукция есть одна из форм умозаключения. (Дедукция происходит от латинского слова «deductio» — выведение.)
Индукцией называется переход от частного утверждения к общему. Индукция есть также одна из форм умозаключения, применяя которую от знания отдельного факта идут к обобщению, к общему положению. (Индукция происходит от латинского слова «inductio» — наведение, побуждение.)
Все формы умозаключения связаны между собой, а потому связаны между собой дедукция и индукция. Одна дедукция (или одна индукция) никогда не может обеспечить познания объективной действительности.
Легкомысленное применение индукции может привести к неправильным выводам. Приведем пример.
Подставив в это выражение вместо п нуль, получим простое число 41. Подставив вместо п единицу, получим 43, т. е. опять простое число. Продолжая подставлять вместо п последовательно 2; 3; 4; 5; 6; 7; 8; 9; 10; 11, получим соответственно 47, 53; 61; 71; 83; 97; 113; 131 151; 173, т. е. опять же числа простые. Можем ли мы теперь быть уверенными в справедливости такого утверждения:
«Выражение 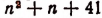
Быть уверенными в справедливости этого утверждения мы не можем, так как полученные выше результаты не являются достаточным основанием для такого утверждения. Они являются лишь основанием для предположения о верности этого утверждения. В действительности более полное исследование выражения 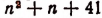
Этот пример показывает, что утверждение может быть верным при одних значениях натурального числа п и неверным при других.
Математическая индукция есть весьма общий метод, позволяющий во многих случаях исследовать законность перехода от частного утверждения к утверждению общему.
Принцип математической индукции можно сформулировать следующим образом.
Теорема о математической индукции
Пусть S(n)—некоторое утверждение, в формулировку которого входнт натуральное число п. Пусть, во-первых, утверждение 
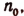
Доказательство:
Допустим, что утверждение S(n) не справедливо при некотором 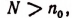
S(N —3) и т. д.
Таким образом (каким бы большим ни было число N), мы рано или поздно, отнимая от этого числа по единице, дойдем до числа 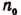

Приведенное доказательство теоремы о математической индукции может показаться некоторым читателям труднопонимаемым. Поэтому ниже приводится несколько упрощенная схема метода математической индукции.
Если в утверждении некоторой теоремы фигурирует целое положительное число п и если из справедливости этой теоремы для какого угодно частного значения п = k следует справедливость ее для значения k + 1, то, коль скоро это утверждение справедливо для п — 1, оно будет справедливо для любого целого положительного числа п.
Здесь дело обстоит так. Сначала мы убеждаемся в том, что теорема верна при п = 1. Затем, предполагая, что она верна для какого угодно частного значения п = k, доказываем ее справедливость для п = k + 1.
После этого рассуждаем так: поскольку теорема верна для п = 1, значит, она будет верной и для п — 1 + 1, т. е. для п = 2. Поскольку она верна для п = 2, она будет верной и для п = 2 + 1, т. е. для п = 3 и т. д.
Применение метода математической индукции
Примеры:
1. Доказать, что
Этой формулой утверждается следующее: для того чтобы найти сумму кубов нескольких первых натуральных чисел, надо последнее из них умножить на число, большее его на единицу, полученное произведение разделить на 2 и возвести в квадрат.
Доказательство:
1. При п = 1 утверждение справедливо,
так как
2. Допустим, что утверждение справедливо при п = k, т. е
Утверждение оказалось верным и для п =k+1. Следовательно, теорема верна при всяком целом положительном значении п.
Доказательство:
1. При п = 1 утверждение справедливо, так как
2. Допустим, что утверждение справедливо при п = k, т. е.
Утверждение оказалось верным и для п = k + 1. Следовательно, формула верна при всяком целом положительном значении п.
3. Доказать, что при п > 1
Доказательство:
При п = 2 утверждение справедливо.
Действительно,
Итак, оказалось, что
Но 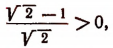
Докажем, что тогда будет справедливым и неравенство:
К обеим частям неравенства (I) прибавим по 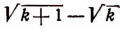
Но 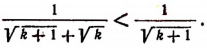
что и требовалось доказать,
Теперь мы видим, что утверждение (А) оказалось верным и для n=k+1. Следовательно, это утверждение справедливо при всяком целом положительном значении n, большем двух.
Существует очень много и других теорем, которые успешно доказываются с помощью метода математической индукции. Некоторые из таких теорем встретятся нам в последующих главах.
Доказательство неравенства
Иногда приходится применять метод математической индукции в несколько усложненной форме. Покажем это на примере. Пусть требуется доказать следующее неравенство:
где 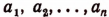
(Выражение 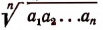
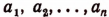

Во-первых, покажем справедливость неравенства (А) при n = 2.
Значит, при n = 2 неравенство (А) справедливо. Теперь докажем следующую лемму.
Лемма:
Если неравенство (А) верно при п = k, то оно будет верно при n=2k.
Доказательство:
Пользуясь свойствами арифметических корней, получим:
(Мы здесь воспользовались доказанным выше неравенством:
Поскольку мы предположили неравенство (А) верным при n = k, постольку
Учитывая эти два последних неравенства и неравенство (В), получим:
Итак, предполагая, что неравенство (А) справедливо при п = 2k, мы доказали, что оно будет справедливым и при п = 2k. Но ранее было доказано, что неравенство (А) справедливо при п = 2. Следовательно, оно будет справедливым и при п = 4,8,16, 32,…, т. е. при 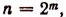
Теперь перейдем к доказательству неравенства (А) для любого натурального числа п.
Пусть п есть любое натуральное число. Если окажется, что п есть целая степень числа 2, то для такого п, как это уже было доказано, неравенство (А) справедливо. Если же п не есть целая степень числа 2, то к n всегда можно прибавить такое число q, что п+ q станет целой степенью числа 2. Итак, положим, что
Тогда получим неравенство:
справедливое при любых положительных 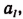
Это следует из того, что число п + q есть целая степень числа 2. Положим, что
Тогда получим последовательно:
что и требовалось доказать.
Значит, неравенство (А) справедливо при всяком натуральном п.
Метод математической индукции
Метод доказательства, называемый методом математической индукции, основан на следующем принципе, который является одной из аксиом арифметики натуральных чисел.
Предложение 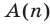
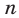
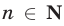
а) предложение 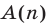
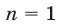
б) из предположения, что 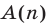
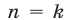
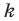
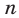
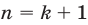
Этот принцип называется принципом математической индукции.
Под методом математической индукции понимают следующий способ доказательства: во-первых, проверяют истинность высказывания 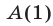
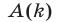
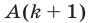
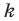
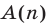
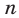
Пример:
Методом математической индукции доказать равенство
Доказательство:
При 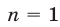
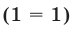
полученного из (1) заменой 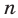
Прибавляя к обеим частям (1) слагаемое 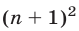
Преобразуя правую часть (3), получаем
Таким образом, равенство (2) является верным, и поэтому формула (1) доказана для любого
Дадим другое доказательство формулы (1), используя символ 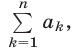
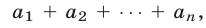
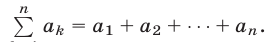
Полагая в (4) 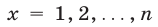
Левая часть (5) равна 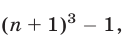
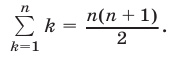
откуда следует равенство (1).
Пример:
Доказать, что для любых 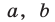
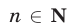
Правую часть формулы (6) называют разложением бинома, числа 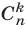
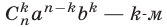
Доказательство. Воспользуемся методом математической индукции. При 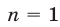
Предполагая справедливым равенство (6), докажем, что верна формула
Умножая обе части равенства (6) на 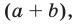
Следовательно,
Сравнивая правые части равенств (8) и (9), заключаем, что для доказательства формулы (8) достаточно показать, что
Используя (7), находим
Равенство (10) доказано и поэтому справедливо равенство (8). Итак, формула (6) верна при любом 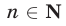
т.е.
Поэтому формулу (6) можно записать в виде
Из (11) следует, что 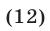
Возможно вам будут полезны эти страницы:
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института