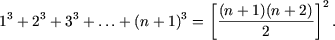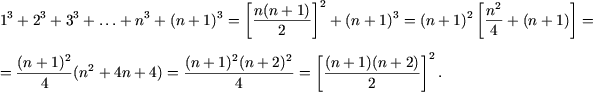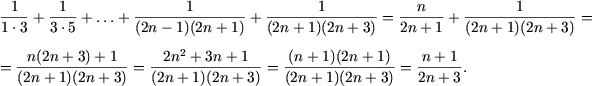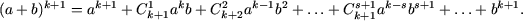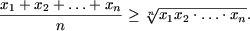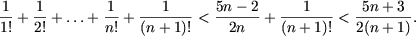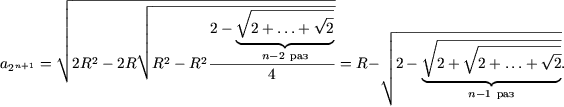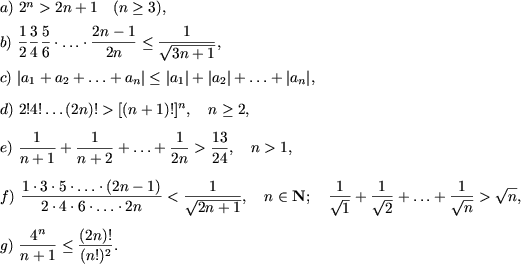Докажите по индукции что для любого натурального n выполняется равенство
Докажите по индукции что для любого натурального n выполняется равенство
Применяя метод математической индукции, доказать, что для любого натурального n справедливы следующие равенства:
а) ;
б) .
а) При n = 1 равенство справедливо. Предполагая справедливость равенства при n, покажем справедливость его и при n + 1. Действительно,
что и требовалось доказать.
б) При n = 1 справедливость равенства очевидна. Из предположения справедливости его при n следует
т. е. утверждение справедливо и при n + 1.
Пример 1. Доказать следующие равенства
Решение. a) При n = 1 равенство примет вид 
Таким образом, согласно методу математической индукции, исходное равенство справедливо для любого натурального n.
Используя предположение индукции, получим
Таким образом, P(n + 1) истинно и, следовательно, требуемое равенство доказано.
Замечание 3. Этот пример можно решить (аналогично предыдущему) без использования метода математической индукции.
c) При n = 1 равенство истинно: 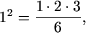
d) При n = 1 равенство справедливо: 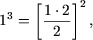
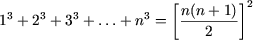
e) Утверждение P(1) справедливо: 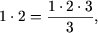
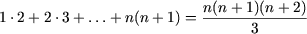
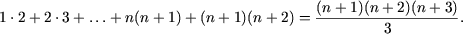
Следовательно, исходное равенство имеет место для любого натурального n.
f) P(1) справедливо: 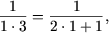
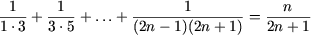
Действительно, учитывая, что P(n) имеет место, получим
Таким образом, равенство доказано.
g) При n = 1 имеем a + b = b + a и, следовательно, равенство справедливо.
Пусть формула бинома Ньютона справедлива при n = k, то есть,
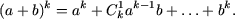
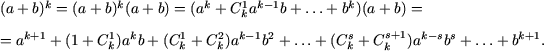
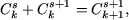
Пример 2. Доказать неравенства
Решение. a) При n = 1 получаем истинное неравенство
Таким образом, если P(n) истинно, то и P(n + 1) истинно, следовательно, согласно принципу математической индукции, неравенство Бернулли справедливо.
Рассмотрим следующие два случая:
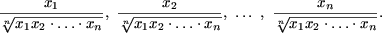
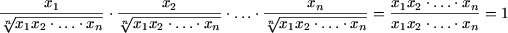
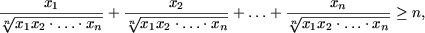
sin 2n a + cos 2n a ≤ 1 и покажем, что имеет место P ( n + 1). Действительно, sin 2(n + 1) a + cos 2(n + 1) a = sin 2n a ·sin 2 a + cos 2n a ·cos 2 a 2n a + cos 2n a ≤ 1 (если sin 2 a ≤ 1, то cos 2 a 2 a ≤ 1, то sin 2 a n О N sin 2n a + cos 2n ≤ 1 и знак равенства достигается лишь при n = 1.
e) При n = 1 утверждение справедливо: 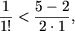
Допустим, что 
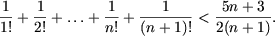
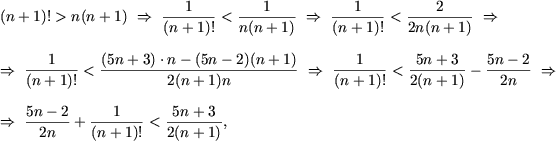
Поскольку при n > 10 имеем 
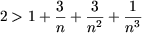
Пример 3. Доказать, что для любого n О N

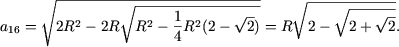
 | (2) |
Как ранее было показано при n = 1, что эта формула справедлива. Пусть (2) выполняется при n = k. Вычислим 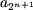
Замечание. Из (2) следует, что длина окружности равна
I. Доказать равенства
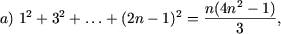 |
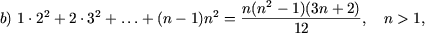 |
 |
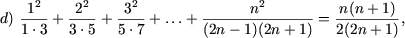 |
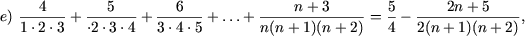 |
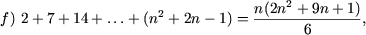 |
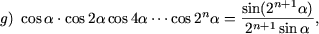 |
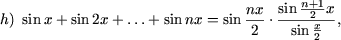 |
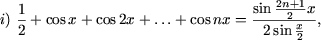 |
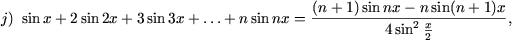 |
 |
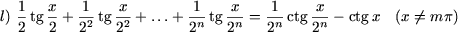 |
 |
II. Доказать неравенства
III. Доказать, что при любом натуральном n число an делится на b
IV. Показать, что 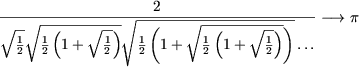
VI. Пусть даны n произвольных квадратов. Доказать, что эти квадраты могут быть разрезаны так, чтобы из получившихся частей можно было образовать квадрат.
Метод математической индукции для чайников
Метод полного перебора конечного числа случаев, исчерпывающих все возможности, называется полной индукцией. Этот метод имеет крайне ограниченную область применения в математике, так как обычно математические утверждения касаются бесконечного множества объектов (например, натуральных чисел, простых чисел, квадратов и т.п.) и перебрать их невозможно.
Основы метода математической индукции
Доказательство с помощью метода математической индукции проводится в два этапа:
Метод математической индукции применяется в разных типах задач:
Ниже вы найдете примеры решения задач, иллюстрирующие применение метода математической индукции, а также ссылки на полезные сайты и учебник и небольшой видеоурок по ММИ.
Математическая индукция: задачи и решения
Доказательство кратности и делимости
$$a_n = 2n^3+3n^2+7n, \quad b=6.$$
Доказательство равенств и неравенств
Задача 5. Доказать равенство
Задача 6. Доказать методом математической индукции:
Задача 7. Доказать неравенство:
Задача 8. Доказать утверждение методом математической индукции:
Задача 9. Доказать неравенство:
Вычисление сумм
Задача 11. Доказать методом математической индукции:
Задача 12. Найдите сумму