Древнегреческий ученый архимед установил что отношение длины окружности к ее диаметру
«Не трогай моих кругов» – число Пи и гибель Архимеда
Продолжаю исторические посты-коротыши, сегодня – об Архимеде. Но перед этим небольшое вступление о событиях куда более недавних, чтобы было понятно, почему этот пост размещаю именно сегодня.
В 1988 году американский физик Ларри Шоу заметил, что в американской системе записи дат (месяц / число) дата 14 марта — 3/14 совпадает с числом π и предложил учредить к этой дате математический праздник – День числа π.
Праздник быстро стал популярным и в 2006 году Конгресс США включил его в официальный список американских праздников, а спустя несколько лет решением ЮНЕСКО за ним закрепили международный статус. Ну а в этом году у числа π еще и свой юбилей – 314 лет с того времени, как его придумали. В 1706 году британский математик Уильям Джонс впервые предложил греческую букву π для обозначения отношения длины окружности к её диаметру (поскольку эта буква начальная в греческих словах περιφέρεια — окружность, периферия и περίμετρος — периметр).
Важный момент, Джонс придумал наименование, сама эта величина была известна достаточно давно, просто под более длинным наименованием «величина, равная отношению длины окружности к её диаметру» и т.п.
Ее вычислением занимались тысячелетия назад, еще в Древнем Египте, есть также легенда, что эту постоянную использовали при проектировании Вавилонской башни. Внес свой вклад в ее расчеты известный древнегреческий математик, физик и инженер Архимед.
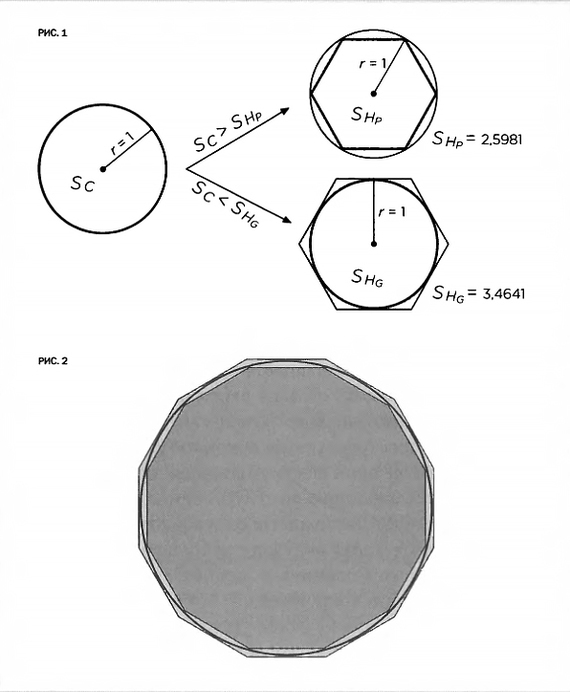
В те времена перед античными математиками встала проблема – как вычислять площадь криволинейных фигур, кругов, овалов и т.п. Частично решить ее удалось с помощью метода исчерпывания (впервые его применил Евклид, а Архимед взял на вооружение и усовершенствовал).
Чтобы его использовать, надо вписать один многоугольник в окружность, а другой описать вокруг нее, тем самым зажав ее между ними. Площадь многоугольников вычислять греки умели, значение площади окружности располагалось где-то в интервале между большим и меньшим многоугольником. Причем, чем больше было сторон у многоугольников, тем меньше был интервал, а следовательно – точнее был результат вычисления площади окружности. И первым эту идею выдвинул как раз Архимед, для начала заменив шестиугольник (который использовали до него) на двенадцатиугольник.
Далее он продолжил увеличивать число сторон и дошел до фигуры с 96 углами. В итоге, была сформулирована т.н. «аксиома Архимеда» о том, что можно найти настолько близкий к площади криволинейной фигуры многоугольник, насколько пожелаешь, но при этом точного результата все равно не достигнешь. Ограничением, по сути, служили цели вычислений, для хозяйственных нужд можно было округлять сильнее, а для научных трактатов – вычислять с максимально возможной точностью. Сам Архимед рассчитал, что соотношение длины окружности и диаметра равно 3( 10)⁄71, он также доказал, что площадь круга равна числу этого соотношения, умноженному на квадрат радиуса круга.
В дальнейшем Архимед еще не раз возвращался к вычислениям методом исчерпывания, стремясь достичь еще большей точности. По легенде, изложенной Плутархом, именно этим ученый занимался и тогда, когда римские войска ворвались в его родной город Сиракузы (хотя немало времени он уделял и вопросам обороны города, но это уже другая история). Он так увлекся, что даже не заметил ворвавшихся солдат. Неожиданно перед ним возник легионер, который потребовал от Архимеда явиться к Марцеллу (командующему римским войском). Погруженный в задачу, Архимед лишь отмахнулся от него – «Не трогай моих кругов», легионер же, офигев от такого отношения, не нашел ничего лучше, как зарубить ученого. Правда, Марцелл за это легионера наказал, поскольку хотел именно пленить Архимеда, которого называл «Бриареем среди геометров».
Свой метод Архимед применял и к объемным фигурам, вычислив соотношение площадей поверхности цилиндра и вписанного в него шара. С этим связана еще одна легенда, что Архимед завещал выбить изображение шара, вписанного в цилиндр на своем надгробии вместо эпитафии. Впрочем, Цицерон утверждал, что своими глазами видел это надгробие, так что, возможно, это не такая уж легенда.
Лига историков
8.3K поста 36K подписчиков
Правила сообщества
— уважение к читателю и открытость
— регулярность и качество публикаций
— умение учить и учиться
— бездумный конвейер копипасты
— публикации на неисторическую тему / недостоверной исторической информации
— простановка тега [моё] на компиляционных постах
— неполные посты со ссылками на сторонний ресурс / рекламные посты
— видео без текстового сопровождения/конспекта (кроме лекций от профессионалов)
— дискуссии на тему постов
— уважение к труду автора
— личные оскорбления и провокации
— неподкрепленные фактами утверждения
Студенты-биологи на полевой практике. Тема: устройство муравейника. После множества обмеров пришли к выводу, что соотношение периметра муравейника в его диаметру примерно равно 3. Этот факт был подан в отчете о практике, почти как научное открытие.
Мне это историю рассказывали как реальную.
Хороший мультик в тему.
Почему пост так поздно появился? 🙁
Вчера надо было этот большой праздник отмечать и ПИть шампанское.
3( 10)⁄71-это скобка порченая, или буква?
Как Пифагор «придумал» музыку и музыку ли он придумал? 😉 Как возникла современная музыкальная система и как в её звуки связаны между собой? Почему нот семь, а на фортепиано семь белых и пять черных клавиш? Где об этом можно прочитать подробнее?
Число Пи
Великий механик: пять коротких историй из жизни Архимеда
История первая. Как взвесить корону
Эту историю все знают из школьных учебников. Правитель Сиракуз (города на Сицилии, где, собственно, и жил Архимед) Гиерон заподозрил, что ювелир, изготовивший ему новую корону, украл часть золота, заменив его серебром. И попросил Архимеда внести ясность в этот вопрос, не разрушая саму корону. Согласно легенде, мудрец долго искал способ как измерить плотность материала короны и в результате, открыл свой знаменитый закон: каждое тело, погруженное в жидкость, теряет столько своего веса, сколько весит вытесненная им жидкость.
Я тоже помню эту историю по школе. Но как мы, школьники, представляли себе процесс экспертизы короны. Архимед ставит сосуд, наполненный водой до краев, в таз, потом погружает в сосуд корону и замеряет, сколько воды вылилось, узнав тем самым ее объем. Потом взвесил корону, узнал ее массу. Поделил массу на объем вылитой воды, узнал плотность материала, сравнил с плотностью золота… Вопросом, откуда Архимед знал значение плотности золота в школе я не задавался.
Уже позже я услышал совсем другое описание этого эксперимента. Архимед взял рычажные весы, на один конец поместил корону, на другую некий вес, равный ей (например, песок). Потом поднес снизу к короне полное ведро воды и погрузил ее в ведро, не отцепляя от весов. Корона, понятно, потеряла часть своего веса и, чтобы снова уравновесить планку, груз надо было передвинуть ближе к центру весов. Замерив расстояние, на которое пришлось сдвигать противовес, Архимед повторил опыт с куском чистого золота, равным тому, что выдали ювелиру. Иначе говоря, Архимед придумал простой, но действенный способ сравнения плотностей разных веществ.
Легенда гласит, что опыт разоблачил жульничество ювелира, потому что противовес пришлось сдвигать иначе. Впрочем, это имело значение для Гиерона, а для науки, конечно, важнее сам принцип, который стал основным законом гидростатики.
История вторая. Как перевернуть корабль
Сам рычаг был известен человечеству задолго до Архимеда (например, строителям египетских пирамид). Но именно Архимед сформулировал первую механико-математическую теорию рычага в трактате «О равновесии плоских фигур» и успешно применял ее на практике, создавая довольно сложные рычажные конструкции.
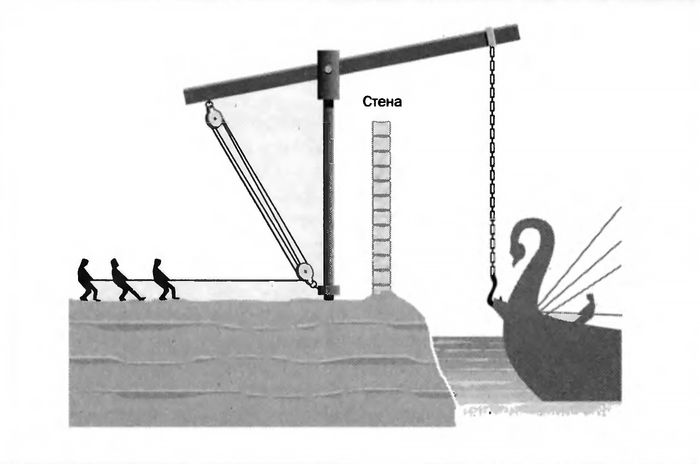
Когда по приказу все того же Гиерона был построен тяжелый многопалубный корабль «Сиракузия» (считается, что он весил более полутора тысяч тонн), встала проблема – как спустить его на воду, не разломав при этом. Понятно дело, снова привлекли Архимеда. В итоге, мудрец соорудил грузоподъёмное устройство, состоящее из собранных в подвижную и неподвижную обоймы блоков, последовательно огибаемых канатом – полиспаст.
По легенде, с помощью этого устройства он смог в одиночку приподнять корабль и перетащить его к воде. Тогда, дескать, он и выдал свой знаменитый афоризм.
Так это или нет, но Архимеда принято считать изобретателем этого устройства, которое по сей день широко используется, причем не только для перемещения грузов. Кстати, по другой легенде, когда римляне осадили Сиракузы, полиспастам нашлось и другое применение: защитники города цепляли крюками борта римских кораблей, приближавшихся к городским стенам и с помощью полиспастов (к которым крепились канаты с крюками) поднимали и переворачивали их. Такие устройства называли «коготь Архимеда».
История третья. Тела небесные
В 1900 году водолазы обнаружили в Эгейском море затонувший античный римский корабль. В течение следующего года с корабля подняли массу артефактов, самый известный получил название Антикитерского механизма. Это устройство и история его изучения заслуживают отдельного поста. Здесь же ограничусь кратким определением: он считается самым древним механическим вычислительным устройством, использовался для расчёта конфигурации движения всех известных в древности планет, включая Марс, Юпитер, Сатурн. Причем тут Архимед? Дело в том, что такое сложное устройство «на пустом месте» не построить, и одним из предшественников его создателей был как раз мудрый грек из Сиракуз.
Астрономия не относилась к главным научным интересам Архимеда. Но он все же написал астрономический трактат «О строении сфер», который, увы, до нас не дошел. Поэтому о его концепции мироустройства мы знаем только со слов других. Архимед в целом был согласен с геоцентрической картиной мира от Аристотеля, где в центре мироздания расположена Земля. Но при этом он считал, что Венера, Марс и Меркурий – обращаются вокруг Солнца и уже вместе с ним – вокруг Земли. В общем система получалась сложная, и чтобы сделать ее более наглядной Архимед (по свидетельству Цицерона) построил механическую модель движения Солнца, Луны, планет и звезд. Модель представляла собой большую металлическую конструкцию и называлась – планетарий.
Причем, они не просто двигались в произвольном порядке, модель Архимеда позволяла рассчитывать фазы Луны и предсказывать даты затмений. По крайней мере, так уверяли очевидцы. После того, как римляне все-таки взяли Сиракузы (Архимед погиб во время штурма), планетарий в числе трофеев увезли в римский храм Доблести. И если одних этот трофей просто развлекал, то других, видимо, подтолкнул к созданию аналогов и даже более сложных вещей, что в итоге и вылилось в создание римлянами Антикитерского механизма. Но это уже исключительно моя версия.
История четвертая. Простые вещи
Когда мы говорим о наследии Архимеда, надо помнить, что оно нас окружает в буквальном смысле слова. Я уже писал, что он написал математическую теорию рычага. Но это не все. Его считают автором теории пяти механизмов, известных в его время и именуемых «простые механизмы». Это – рычаг, наклонная плоскость, блок, лебедка и бесконечный винт. Последний механизм он изобрел и одновременно придумал резьбовое соединение элементов – винта и гайки. А теперь попробуйте представить себе жилье, в котором нет ни одного резьбового соединения. Так что все мы постоянно пользуемся плодами научного наследия Архимеда, даже не подозревая об этом.
История пятая. Математические достижения
Математика была главной наукой в жизни Архимеда. И он добился в этой области потрясающих результатов. О его вычислениях числа π я рассказывал в одном из постов. Есть мнение, что он продолжал эту работу, когда римляне ворвались в Сиракузы и не пожелал прерваться, что и стало причиной его гибели. Но вот сам Архимед считал своим главным математическим достижением – расчет соотношения объемов цилиндра и вписанного в него шара (оно равно 3/2). Это при условии, что диаметр шара равен диаметру основания цилиндра и его высоте. Такое же соотношение и у площадей их поверхностей. Кому-то может показаться, что это не такая уж сложная задача. Но, напомню, в то время не было алгебры, греки не знали десятичных дробей, не оперировали понятием ноля, иррациональных чисел и многими другими привычными нам элементами математики. Так что решение этой задачи вылилось в целый трактат «О шаре и цилиндре», который содержал еще кучу важной геометрической информации, полученной Архимедом в качестве промежуточных результатов.
Архимед настолько гордился этой работой, что просил выбить на своей могиле изображение цилиндра с вписанным в него шаром с отношением их объемов. Много лет спустя, посетив Сиракузы, Цицерон утверждал, что нашел это надгробие с выбитым кубом, в который были вписаны цилиндр и шар. И не просто нашел, а распорядился привести заросшую могилу в порядок и ухаживать за ней. Увы, затем все вновь пришло в запустение, и могила была повторно утеряна, теперь уже навсегда.
Сегодня память об Архимеде живет в виде множества картин, почтовых марок и проч. А еще профиль Архимеда и его слова «Превзойти свою человеческую ограниченность и покорить Вселенную» выбиты на медали лауреата премии Филдса – аналога Нобелевской премии для математиков.
Практическая работа «Практические приемы вычислений с приближенными данными. Вычисление погрешности при решении практических задач»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Тема: «Практические приемы вычислений с приближенными данными. Вычисление погрешности при решении практических задач»
Специальность: 080110 Экономика и бухгалтерский учет (по отраслям)
100701 Коммерция (по отраслям)
Цель: студент должен уметь вычислять приближенные значения
№ 1. 1) Площадь океанов равна:
Атлантического. 93 363 » » »
Северного Ледовитого..13 100 » » »
Вычислить общую площадь этих океанов в миллионах квадратных километров, округлив данные в условии числа.
2) Округлить до тысяч следующие числа: 10 834 650; 4 354 160; 4 793 500; 6 381 480. Вычислить погрешность, допущенную при округлении.
4) Округлить до десятых долей следующие дробные числа: 12,39; 87,15; 279,68; 156,44; 60,52; 3,25; 1,408. Вычислить погрешность, допущенную при округлении.
№ 2. 1) Вычислить приближённые частные с точностью до целой единицы:
15139 : 25; 78,66 : 0,13; 78,66 : 0,013.
2) Вычислить приближённые частные с точностью до 0,1:
14 : 3; 5,4 : 1,7; 15,4 : 4.
3) Вычислить приближённые частные с точностью до 0,01 :
417 : 35; 17,51 : 6; 2,25 : 0,07; 39,5 :1,3.
№ 3. Сколько квадратных километров площади приходится на одного жителя каждой из указанных частей света, если:
в Азии на 43 883 тыс. кв. км площади приходится 1 535 000 тыс. человек,
в Африке на 30 284 тыс. кв. км площади приходится 224 000 тыс. человек,
в Европе на 10 498 тыс. кв. км площади приходится 569 000 тыс. человек.
Вычисления произвести с точностью до 0,01 кв. км.
№ 5. Выразить приближённо десятичной дробью число 5 2 / 7 с тремя верными цифрами. Вычислить абсолютную погрешность полученного приближённого значения.
№ 6. Сравним время на стенных и ручных часах. Пусть стенные часы показывают 2 часа 14 мин. (пополудни). Можно ли считать цифру 4 верной?
Пусть ручные часы в тот же момент показали 2 часа 13 мин. 15 сек. Можно ли считать цифру 5 верной? При решении задачи предполагается, что те и другие часы правильны.
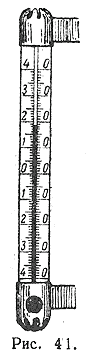
№ 7. 1) На наружном термометре столбик подкрашенного спирта находится между 18 и 19 делениями выше нуля (рис. 41). Ученик записал показания термометра числом 18,5°. Назовите верные цифры, в этом числе. Как записать, что допущенная погрешность не превышает 0,5°?
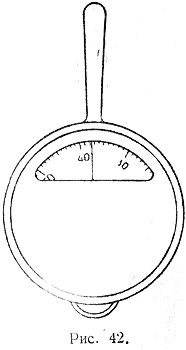
2) На рисунке 42 изображена шкала курвиметра. При обведении части контура некоторой фигуры черта курвиметра оказалась между 37 и 38 делениями шкалы. Сколько сантиметров прошло колесо курвиметра, если каждое деление шкалы курвиметра соответствует 1 см длины? Ученик записал показание курвиметра 37,5 см. Назовите верные цифры в полученном числе. Как записать, что допущенная погрешность не превышает 0,5 см?
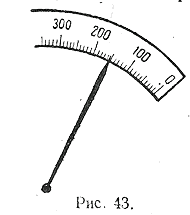
№ 8. На весах взвешено 150 г конфет. Рассмотрите рисунок части шкалы весов (рис. 43). Какой наименьший и наибольший возможен вес данной покупки и какова наибольшая абсолютная погрешность при взвешивании на этих весах?
№ 9. 1) Ученик должен начертить план класса. Рулеткой он измерил длину а и ширину b и нашёл а ≈ 8,50 м и b ≈ 6,20 м. Назовите верные цифры в полученных числах. Как запирать, что возможная погрешность при измерении не превышает 5 см?
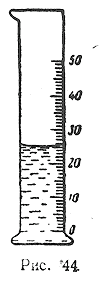
2) Измеряя мензуркой (рис. 44) объём жидкости, ученик получил 26 куб. см. Назовите в полученном числе верные цифры. Какую наибольшую погрешность мог допустить ученик при отсчёте на шкале мензурки?
№ 10. 1) Одна из старых русских мер длины—аршин (1 аршин ≈ 71,12 см) выражала приближённо длину шага взрослого человека. Если принять 1 аршин приближённо за 71 см, то какова получится абсолютная погрешность? (Значение 71,12 см при решении задачи примите за точное выражение аршина в метрических мерах.)
2) Одна из старых русских мер веса — пуд — приближённо равна 16,38 кг. Если принять, что 1 пуд ≈ 16,4 кг, то чему равна абсолютная погрешность? (Число 16,38 кг при решении задачи примите за точное выражение пуда в метрических мерах.)
Древнегреческий ученый архимед установил что отношение длины окружности к ее диаметру
§ 37. Понятие о приближённом числе. Абсолютная погрешность.
1009. 1) Площадь океанов равна:
Атлантического. 93 363 » » »
Северного Ледовитого..13 100 » » »
Вычислить общую площадь этих океанов в миллионах квадратных километров, округлив данные в условии числа.
2) Округлить до тысяч следующие числа: 10 834 650; 4 354 160; 4 793 500; 6 381 480. Вычислить погрешность, допущенную при округлении.
3) Округлить до целых единиц следующие дробные числа: 228,7; 142,61; 374,4; 92,5; 93,5; 7 2 /3; 4 1 /5. Вычислить погрешность, допущенную при округлении.
4) Округлить до десятых долей следующие дробные числа: 12,39; 87,15; 279,68; 156,44; 60,52; 3,25; 1,408. Вычислить погрешность, допущенную при округлении.
1010. 1) Вычислить приближённые частные с точностью до целой единицы:
15139 : 25; 78,66 : 0,13; 78,66 : 0,013.
2) Вычислить приближённые частные с точностью до 0,1:
14 : 3; 5,4 : 1,7; 15,4 : 4.
3) Вычислить приближённые частные с точностью до 0,01 :
417 : 35; 17,51 : 6; 2,25 : 0,07; 39,5 :1,3.
1011. Сколько квадратных километров площади приходится на одного жителя каждой из указанных частей света, если:
в Азии на 43 883 тыс. кв. км площади приходится 1 535 000 тыс.человек,
в Африке на 30 284 тыс. кв. км площади приходитсяи 224 000 тыс. человек,
в Европе на 10 498 тыс. кв. км площади приходится 569 000 тыс. человек.
Вычисления произвести с точностью до 0,01 кв. км.
1012. Древнегреческий учёный Архимед установил, что отношение длины окружности к её диаметру больше числа 3 10 /71 и меньше 3 1 /7. Вычислить значения этих дробей с точностью до 0,01.
1013. Выразить приближённо десятичной дробью число 5 2 /7 с тремя верными цифрами. Вычислить абсолютную погрешность полученного приближённого значения.
1014. Сравним время на стенных и ручных часах. Пусть стенные часы показывают 2 часа 14 мин. (пополудни). Можно ли считать цифру 4 верной?
Пусть ручные часы в тот же момент показали 2 часа 13 мин. 15 сек. Можно ли считать цифру 5 верной? При решении задачи предполагается, что те и другие часы правильны.
1015. 1) На наружном термометре столбик подкрашенного спирта находится между 18 и 19 делениями выше нуля (рис. 41). Ученик записал показания термометра числом 18,5°. Назовите верные цифры, в этом числе. Как записать, что допущенная погрешность не превышает 0,5°?
2) На рисунке 42 изображена шкала курвиметра. При обведении части контура некоторой фигуры черта курвиметра оказалась между 37 и 38 делениями шкалы. Сколько сантиметров прошло колесо курвиметра, если каждое деление шкалы курвиметра соответствует 1 см длины? Ученик записал показание курвиметра 37,5 см. Назовите верные цифры в полученном числе. Как записать, что допущенная погрешность не превышает 0,5 см?
1016. На весах взвешено 150 г конфет. Рассмотрите рисунок части шкалы весов (рис. 43). Какой наименьший и наибольший возможен вес данной покупки и какова наибольшая абсолютная погрешность при взвешивании на этих весах?
1017. 1) Ученик должен начертить план класса. Рулеткой он измерил длину а и ширину b и нашёл а ≈ 8,50 м и b ≈ 6,20 м. Назовите верные цифры в полученных числах. Как запирать, что возможная погрешность при измерении не превышает 5 см?
2) Измеряя мензуркой (рис. 44) объём жидкости, ученик получил 26 куб. см. Назовите в полученном числе верные цифры. Какую наибольшую погрешность мог допустить ученик при отсчёте на шкале мензурки?
1018. 1) Одна из старых русских мер длины—аршин (1 аршин ≈ 71,12 см) выражала приближённо длину шага взрослого человека. Если принять 1 аршин приближённо за 71 см, то какова получится абсолютная погрешность? (Значение 71,12 см при решении задачи примите за точное выражение аршина в метрических мерах.)
2) Одна из старых русских мер веса — пуд — приближённо равна 16,38 кг. Если принять, что 1 пуд ≈ 16,4 кг, то чему равна абсолютная погрешность? (Число 16,38 кг при решении задачи примите за точное выражение пуда в метрических мерах.)
1019. Чтобы найти количество зёрен в 1 кг ржи, берут пять проб по 10 г каждую и подсчитывают в каждой количество зёрен. Пусть при подсчетах получились числа: 308, 336 327, 343 и 316. Подсчитайте среднее количество зёрен в 10 г ржи. Установите верные цифры полученного среднего значения. Для проверки верных цифр числа зёрен в 10 г ржи вычислите разность между значениями каждой пробы и найденным средним. Найдите среднее арифметическое этих разностей и по цифре старшего разряда его проверьте правильность взятых верных цифр в среднем значении числа зёрен в 10 кг ржи. Чему считается равной в данном случае абсолютная погрешность результата? Сколько зёрен ржи содержится в 1 кг ржи?
1020. Ученик решил подсчитать число шагов, которое он делает на пути из дома в школу. Один раз он насчитал 950 шагов, другой 938 и в третий—965 шагов. Найдите среднее арифметическое зтих чисел. Вычислите разность между каждым значением слагаемых и средним. Найдите среднее арифметическое вычисленных разностей. Укажите верные цифры приближённого значения числа шагов.