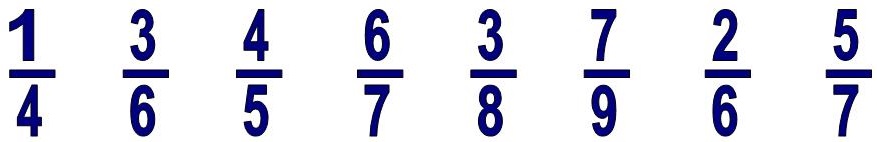Дробь что сверху что снизу

Числитель и знаменатель

Числитель дроби — это число, стоящее в записи обыкновенной дроби над дробной чертой, то есть сверху. Числитель показывает количество долей.

Знаменатель дроби — это число, стоящее в записи дроби под дробной чертой, то есть снизу. Знаменатель показывает, какие это доли и на сколько равных частей разделена единица.

Дробная черта — это горизонтальная черта в записи дроби, которая отделяет числитель и знаменатель друг от друга.

Вместе, числитель и знаменатель дроби, называются членами дроби.

Условились считать, что дробная черта означает деление верхнего числа на нижнее, поэтому:

Любую операцию деления можно записать в виде дроби. И наоборот, любую дробь можно записать в виде операции деления.

Как читать запись обыкновенных дробей

По этому правилу читаются все обыкновенные дроби.

Пример 1. Прочитайте дробь , назовите числитель и знаменатель.

Пример 2. Прочитайте дробь .

Пример 3. Прочитайте дробь .

Источник

Дроби и доли.

Дроби самая сложная тема для учеников начальных классов. Но даже самая трудная тема может стать простой и понятной. Для обучения детей нужно использовать фантазию и элементы игры. А главное – сохранять спокойствие.

В серьезных учебниках по математике есть знаки: и сложение, и вычитание, и умножение. А вот, привычного нам, с вами знака деления (:) – нет. Получается, что знаком деления (:) пользуются только ученики начальной школы? На самом деле – нет. Только этот знак можно писать и по-другому, вот такой чертой, она пишется посередине клетки:

Вот это все – деление.
Деление можно записывать не двумя точками, а горизонтальной полоской.
Так вот: любая математическая запись, в которой присутствует знак деления в виде черточки, называется дробью.
Слово «дробь» говорит само за себя – оно обозначает дробление или деление.
Для записи дробей используются цифры и черта, которую называют дробной.

Вы когда-нибудь видели военный парад? Идут солдаты стройными рядами, а впереди человек со знаменем (флагом) – знаменосец! И по знамени легко понять, к какому роду войск принадлежат эти солдаты. У дроби тоже есть «знаменосец» — это главное число, которое обозначает, на сколько равных частей разделили целое (предмет, фигуру или величину).

«Знаменосец» пишется под дробной чертой и называется ЗНАМЕНАТЕЛЬ.

А число, над чертой показывает, сколько таких частей взяли (или закрасили, или съели). Это число называют ЧИСЛИТЕЛЕМ.

читается – две третьих, можно заменить по-другому — 2 : 3.

Рассмотрим еще одно число: раньше мы не могли на уроке математики 1 разделить на 2. А теперь – умеем: 1 разделить на 2 – это не что иное, как одна вторая. Что же это значит? Если в математике мы с вами не делали этого ни разу, то в жизни вы это делаем постоянно. Предположим, у вас есть яблоко. И вам нужно разделить его между вами и другом. Т.е. одно яблоко разделить на 2.

Так что же за число такое – одна вторая, во-первых, это дробь потому что присутствует знак деления, во-вторых, оно меньше единицы.
Потому что нельзя один разделить на 2, чтобы получилось что-то больше 1.
В-третьих, оно обозначает, что мы целое разделили на 2 и взяли себе одну такую часть.

Давайте посмотрим на число:

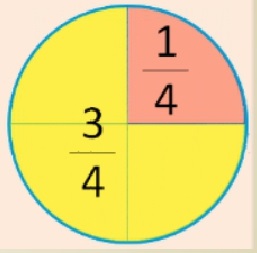
По правилу, которое мы с вами вывели: три четвертых – это тоже самое, что три разделить на 4.

Давайте посмотрим, как это понять. Круг разделим на 4 равные части.
3 части закрасим желтым цветом. Это и есть три четвертых. Что же это значит?
Во-первых, это тоже дробь.
Во-вторых, она тоже меньше единицы.
И она обозначает, что круг мы разделили на 4 части
и закрасили желтым цветом – 3 таких части.

Итак,
как вы уже поняли: любая дробь будет иметь черту.
Ее так и называют – дробная черта. И обязательно будет стоять какое-то число над чертой и какое-то число под чертой.

Давайте научимся, как правильно читать дроби.
Читают их так: верхнее число всегда будет отвечать на вопрос: сколько?, а нижнее будет отвечать на вопрос: какая? или каких?

Сколько? – три, каких? – восьмых – три восьмых,
Сколько? – семь, каких? – девятых – семь девятых,
Сколько? – две, каких? – шестых – две шестых,
Сколько? – пять, каких? – седьмых – пять седьмых.

У чисел, которые вверху и внизу дроби есть свое научное название: верхнее число называется числитель, а нижнее – знаменатель.
Постарайтесь запомнить это. Это важно! Числитель – наверху, знаменатель – внизу.
Знаменатель показывает на сколько частей мы разделили наше целое, а числитель показывает – сколько частей целого мы с вами взяли.

Чтобы лучше запомнить, где числитель, где знаменатель, есть простая напоминалочка:
«ЧЕЛОВЕК ХОДИТ ПО ЗЕМЛЕ».
Ч – числитель – «над», З – знаменатель «под».

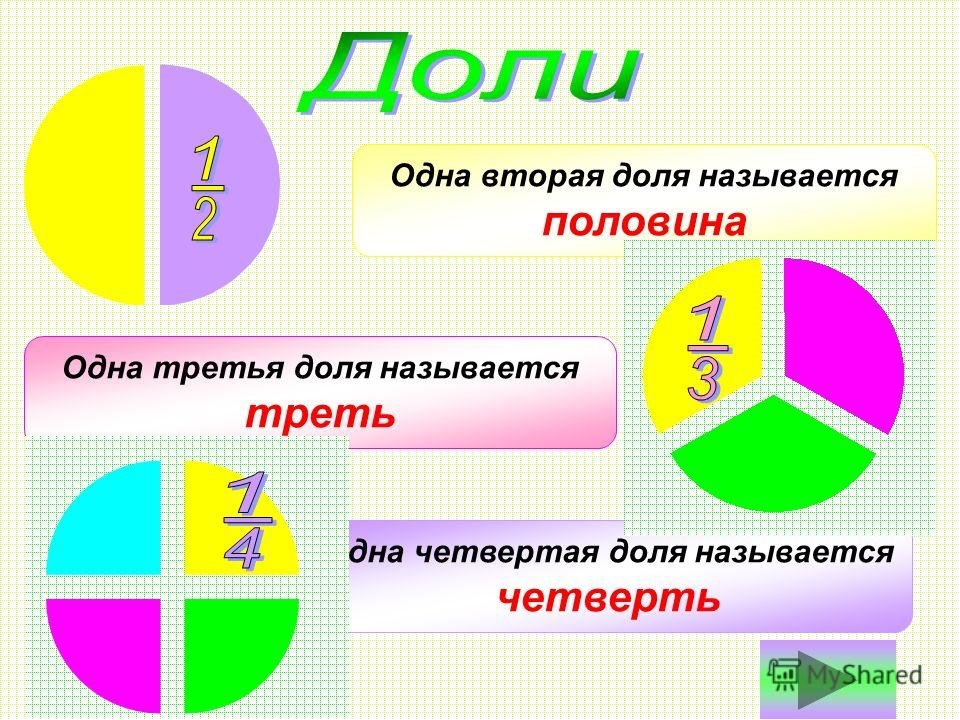
Есть одна разновидность дробей, которую в начальной школе выделяют в отдельную группу. Такие дроби называют долями. Если вам встретилось слово «доля», знайте, что это та же самая дробь, но только у нее числитель равен единице.

Мы постоянно сталкиваемся с ними в жизни.

Чаще всего мы встречаемся в жизни именно с половиной:

пол яблока — это одна вторая яблока, пол стакана – это одна вторая стакана.

Так же мы знакомы с одной третьей:

– это не что иное, как треть.
Треть грейфрута – это значит, разделили грейфрут на 3 части и взяли одну.

Точно так же мы с вами называем одну четвертую четвертью.
Например – школьная четверть. Мы с вами делим учебный год на 4 части и берем одну часть. Это и есть – четверть.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.9 / 5. Количество оценок: 81

Источник

Обыкновенные дроби

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Доля целого

Доля — это каждая равная часть, из суммы которых состоит целый предмет.

Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.

У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.

Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.

Чтобы быстрее запомнить соотношения частей и целого, можно использовать наглядную табличку:

Понятие дроби

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:

Виды дробей:

Какие еще бывают дроби:

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3\5.

Выделение целой части из неправильной дроби — это запись неправильной дроби в виде суммы натурального числа и правильной дроби. Например, 11/5 = 2 + 1/5.

Как устроена обыкновенная дробь

Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.

Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.

Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.

Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.

Черта между числителем и знаменателем — символ деления.

Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.

Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.

Как устроена десятичная дробь

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Свойства дробей

Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:

где a, b, k — натуральные числа.

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:

У нас есть отличные курсы по математике для учеников с 1 по 11 классы, записывайтесь!

Действия с дробями

С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.

Сравнение дробей

Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.

Сравним 1/5 и 4/5. Как рассуждаем:

Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.

Пример. Сравнить 2/7 и 1/14.

Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.

Чтобы сравнить дроби с разными числителями и знаменателями, нужно:

Чтобы привести дроби к наименьшему общему знаменателю, нужно:

Сокращение дробей

Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.

Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.

В этом примере делим обе части дроби на двойку.

Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.

Сложение и вычитание дробей

При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.

Не забудьте проверить, можно ли сократить дробь и выделить целую часть.

При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).

Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.

НОК (15, 18) = 3 * 2 * 3 * 5 = 90

Полученные числа запишем справа сверху над числителем.

Ход решения одной строкой:

Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:

Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.

Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.

Умножение и деление дробей

Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:

Не забываем про сокращение. Это может облегчить вычисления.

Чтобы умножить два смешанных числа, надо:

Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:

Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.

Числа, произведение которых равно 1, называют взаимно обратными.

Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.

Для деления смешанных чисел необходимо:

Источник

Числитель и знаменатель дроби

Числитель и знаменатель дроби. Виды дробей. Продолжаем рассматривать дроби. Сначала небольшая оговорка – мы, рассматривая дроби и соответствующие примеры с ними, пока будем работать только с числовым её представлением. Бывают ещё и дробные буквенные выражения (с числами и без них). Впрочем, все «принципы» и правила также распространяются и на них, но о таких выражениях поговорим в будущем отдельно. Рекомендую посетить эту страницу и изучать (вспоминать) тему дробей шаг за шагом.

Самое главное понять, запомнить и осознать, что ДРОБЬ – это ЧИСЛО.

Обыкновенная дробь – это число вида:

Число расположенное «сверху» (в данном случае m) называется числителем, число расположенное снизу (число n) называется знаменателем. У тех, кто только коснулся темы частенько возникает путаница – что как называется.

Вот вам приёмчик, как навсегда запомнить – где числитель, а где знаменатель. Данный приём связан со словесно-образной ассоциацией. Представьте себе банку с мутной водой. Известно, что по мере отстоя воды чистая вода остаётся сверху, а муть (грязь) оседает, запоминаем:

ЧИССС тая вода ВВЕРХУ ( ЧИССС литель сверху)

Гря ЗЗЗННН ая вода ВНИЗУ ( ЗННН аменатель внизу)

Так что, как только возникнет необходимость вспомнить, где числитель, а где знаменатель, то сразу зрительно представили банку с отстоянной водой, в которой сверху ЧИСтая вода, а снизу гряЗНая вода. Есть и другие приёмы для запоминания, если они вам помогут, то хорошо.

Примеры обыкновенных дробей:

Что означает горизонтальная черточка между числами? Это не что иное, как знак деления. Получается, что дробь можно рассматривать как бы как пример с действием делением. Просто записано это действие вот в таком виде. То есть, верхнее число (числитель) делится на нижнее (знаменатель):

Кроме того, есть ещё форма записи – дробь может записываться и так (через косую черту):

1/9, 5/8, 45/64, 25/9, 15/13, 45/64 и так далее…

Можем записать вышеуказанные нами дроби так:

Результат деления, как известно это число.

Уяснили – ДРОБЬ ЭТО ЧИСЛО.

Как вы уже заметили, у обыкновенной дроби числитель может быть меньше знаменателя, может быть больше знаменателя и может быть равен ему. Тут присутствует множество важных моментов, которые понятны интуитивно, без каких-либо теоретических изысков. Например:

1. Дроби 1 и 3 можно записать как 0,5 и 0,01. Забежим немного вперёд – это десятичные дроби, о них поговорим чуть ниже.

2. Дроби 4 и 6 в результате дают целое число 45:9=5, 11:1 = 11.

3. Дробь 5 в результате даёт единицу 155:155 = 1.

Какие выводы напрашиваются сами собой? Следующие:

1. Числитель при делении на знаменатель может дать конечное число. Может и не получится, разделите столбиком 7 на 13 или 17 на 11 — никак! Делить можно бесконечно, но об этом также поговорим чуть ниже.

2. Дробь в результате может дать целое число. Следовательно и любое целое число мы можем представить в виде дроби, вернее бесконечного ряда дробей, посмотрите, все эти дроби равны 2:

Ещё! Любое целое число мы всегда можем записать в виде дроби – само это число в числителе, единица в знаменателе:

3. Единицу мы всегда можем представить в виде дроби с любым знаменателем:

*Указанные моменты крайне важны для работы с дробями при вычислениях и преобразованиях.

А теперь о теоретическом разделении обыкновенных дробей. Их разделяют на правильные и неправильные.

Дробь у которой числитель меньше знаменателя называется правильной. Примеры:

Дробь у которой числитель больше знаменателя или равен ему называется неправильной. Примеры:

Смешанная дробь (смешанное число).

Смешанной дробью называется дробь, записанная в виде целого числа и правильной дроби и понимается как сумма этого числа и дробной его части. Примеры:

Смешанную дробь всегда можно представить в виде неправильной дроби и наоборот. Идём далее!

Десятичные дроби.

Выше мы их уже затронули, это примеры (1) и (3), теперь подробнее. Вот примеры десятичных дробей: 0,3 0,89 0,001 5,345.

Дробь, знаменатель которой есть степень числа 10, например 10, 100, 1000 и так далее, называется десятичной. Записать первые три указанные дроби в виде обыкновенных дробей несложно:

Четвёртая является смешанной дробью (смешанным числом):

Десятичная дробь имеет следующую форму записи — с начала целая часть, затем разделитель целой и дробной части точка или запятая и затем дробная часть, количество цифр дробной части строго определяется размерностью дробной части: если это десятые доли, дробная часть записывается одной цифрой; если тысячные — тремя; десятитысячные — четырьмя и т. д.

Данные дроби бывают конечными и бесконечными.

Примеры конечных десятичных дробей: 0,234; 0,87; 34,00005; 5,765.

Примеры бесконечных. Например число Пи это бесконечная десятичная дробь, ещё – 0,333333333333…. 0,16666666666…. и прочие. Также результат извлечения корня из чисел 3, 5, 7 и т.д. будет являться бесконечной дробью.

Дробная часть может быть цикличная (в ней присутствует цикл), два примера выше именно такие, ещё примеры:

0,123123123123…. цикл 123

0,781781781718…. цикл 781

0,0250102501…. цикл 02501

Записать их можно как 0,(123) 0,(781) 0,(02501).

Число Пи не является цикличной дробью как и, например, корень из трёх.

Ниже в примерах, будут звучать такие слова как «переворачиваем» дробь – это означает что числитель и знаменатель меняем местами. На самом деле у такой дроби есть название – обратная дробь. Примеры взаимно-обратных дробей:

Источник