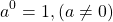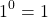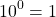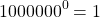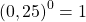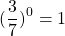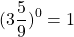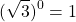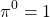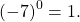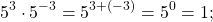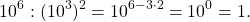Дробь в нулевой степени чему равно
Степень 0
В алгебре возведение с нулевую степень встречается часто. Что такое степень 0? Какие числа можно возводить в нулевую степень, а какие — нет?
Любое число в нулевой степени, за исключением нуля, равно единице:
Таким образом, какое бы число ни возвели в степень 0, результат всегда получится одинаковый — единица.
И 1 в степени 0, и 2 в степени 0, и любое другое число — целое, дробное, положительное, отрицательное, рациональное, иррациональное — при возведении в нулевую степень дает единицу.
Единственное исключение — нуль.
Нуль в нулевой степени не определен, такое выражение не имеет смысла.
То есть в нулевую степень можно возводить любое число, кроме нуля.
Если при упрощении выражения со степенями получается число в нулевой степени, его можно заменить единицей:
Если при упрощении получается переменная или выражение с переменными в нулевой степени, пишем дополнительное условие — основание степени должно быть отличным от нуля:
Возведение дроби в степень правило, как возвести алгебраическую дробь в степень, калькулятор примеров, свойства дробных степеней, как решать примеры со степенью
В алгебре, пожалуй, одной из самых распространённых операций является возведение дроби в степень. Это довольно простое действие, которое похоже на умножение. Обучают ему на уроках математики в восьмом классе. Вычисление ответа заключается в различных нюансах, зависящих от типа дробного выражения. Но при этом существует универсальное правило. Используя его, можно находить как положительную, так и отрицательную степень.
Понятие степени
Представления о степени сложились ещё во времена существования Древнего Египта. Впервые упоминание о её вычислении встречается в знаменитом учебнике по математике Диофанта Александрийского «Арифметика». В своих трудах он описывает понятие как некоторое количество единиц, из которых состоят любые числа, увеличивающиеся до бесконечности. Он выделяет:
Французский учёный Никола Шюке дополнил этот степенной ряд, введя отрицательный параметр. Современное же обозначение степени предложил Рене Декарт. В «Геометрии» он использовал верхний надстрочный знак для указания величины степени. Что интересно, квадрат математик продолжал обозначать как произведение чисел, то есть в виде n * n. И только потом Лейбниц настоял на универсальной записи для любого возведения в степень.
Под операцией возведения понимается бинарное действие, определяемое в результате умножения числа на себя. То есть справедлива следующая запись: d i = d * d* d *… * dk, где k — число, обозначающее количество перемножаемых чисел, равное n. Например, 11 2 = 11 * 11 = 121. Степень, присущая числу, может быть отрицательной, рациональной, десятичной, вещественной и даже комплексной. Фактически получается, что для того, чтобы посчитать степень числа, его нужно умножить на себя столько раз, сколько указано в степенном показателе.
Правило возведения дроби
В основе правила возведения дроби в степень лежит её определение с дробным показателем. Согласно ему, для решения задачи нужно отдельно возвести сначала числитель выражения, а затем знаменатель, не меняя занимаемые ими позиции. Например, дробь три шестых во второй степени будет равна: (3/6) 2 = 9/36. Используя свойства сокращения дробей, числитель и знаменатель можно разделить на девять. В итоге получится равенство: (3/6) 2 = 1/4.
Доказать это правило можно выполнив элементарные алгебраические действия. Для рассмотренного примера, согласно правилу арифметики, сначала необходимо выполнить деление, а после возведение в степень. Так, три разделить на шесть будет равно: 3/6 = 1/2 = 0,5. Затем полученное число следует возвести в квадрат: 0,5 2 = 0,5 * 0,5 = 0,25. Найденный ответ можно переписать в виде дроби 1/4, которая при сравнении полностью совпадает с ранее вычисленной.
Чтобы убедиться в истинности правила, можно и тут выполнить проверку. Дробь три разделить на пять в степени три можно решить, выполнив сначала деление, а после полученное число возвести в кубическую степень: (11 / 14) 3 = (0,78) 3 = 0,78 * 0,78 * 0,78 = 0,485. Ответ идентичен предыдущему, что и следовало доказать.
Таким образом, алгоритм возведения будет следующим:
Если показатель степени небольшой, то возведение можно выполнить просто умножив дробь на саму себя необходимое число раз. Например, (2/32) 3 = (2/32) * (2/32) *(2/32) = 1/4096. Алгоритм обыкновенного расчёта обычно не вызывает трудности, но часто приходиться иметь дело не только с обыкновенными дробями. При этом степень может быть даже отрицательной.
Но в любом случае нужно помнить, что если верхнюю и нижнюю часть дроби умножить или разделить на одно и то же число, то количественный показатель полученного выражения не изменится. Это важно, так как при возведении приходится часто выполнять преобразования.
Нулевая и отрицательная степень
При вычислении дроби, в показателе которой стоит ноль, исходят из свойств частного степеней с одинаковым основанием.
Ответ на 0 0 может быть любым. Поэтому для избежания путаницы считают, что решение записи 0 0 не имеет смысла, так же как и деление на ноль. Например, (12 / 34) 0 = 12 0 / 34 0 = 1 / 1 = 1 или (-3 / 4) 0 = 1, а вот для (0 / 23) 0 ответ будет не определён.
Рациональный показатель
В состав рациональных чисел входят все целые и дробные значения. По сути, ими называют значения, которые можно представить в виде обыкновенной или отрицательной дроби, как цифру ноль. При этом в числителе находится целое число, а в знаменателе – натуральное. Для того чтобы определить степень, нужно выяснить, что же представляет собой число с показателем в дробной форме.
Примеры решения
Для того чтобы понять и усвоить теорию, нужно попрактиковаться. Начинать необходимо с простых заданий, постепенно переходя к более сложным примерам. Возвести дробь в степень можно и на онлайн-калькуляторах, но желательно уметь выполнять это действие самостоятельно. Из наиболее типичных примеров, охватывающих все возможные ситуации, можно выделить следующие:
В сети существуют сервисы, автоматически выполняющие арифметические операции. Воспользоваться этими сайтами может каждый, имеющий доступ к интернету. Порталы предлагают свои услуги бесплатно. С их помощью можно находить функции, рассчитывать градусы и углы, решать уравнения и неравенства, вычислять дроби и степени.
Для решения дробей со степенями на онлайн-калькуляторах не нужно обладать какими-то особыми знаниями. Всё что требуется от пользователя — вести в предложенную форму задание и нажать кнопку «Рассчитать». Весь процесс вычисления занимает несколько секунд.
Полезной особенностью таких сайтов является и возможность обучиться правилам расчёта, узнать, как должны обозначаться те или иные операции и действия. Из различных калькуляторов можно выделить три наиболее популярных:
Сайты отличаются удобным и понятным интерфейсом. На их страницах содержится кратко изложенная теория, использующаяся для расчётов и типовые примеры.
Понятие степени
Представления о степени сложились ещё во времена существования Древнего Египта. Впервые упоминание о её вычислении встречается в знаменитом учебнике по математике Диофанта Александрийского «Арифметика». В своих трудах он описывает понятие как некоторое количество единиц, из которых состоят любые числа, увеличивающиеся до бесконечности. Он выделяет:
Французский учёный Никола Шюке дополнил этот степенной ряд, введя отрицательный параметр. Современное же обозначение степени предложил Рене Декарт. В «Геометрии» он использовал верхний надстрочный знак для указания величины степени. Что интересно, квадрат математик продолжал обозначать как произведение чисел, то есть в виде n * n. И только потом Лейбниц настоял на универсальной записи для любого возведения в степень.
Под операцией возведения понимается бинарное действие, определяемое в результате умножения числа на себя. То есть справедлива следующая запись: d i = d * d* d *… * dk, где k — число, обозначающее количество перемножаемых чисел, равное n. Например, 11 2 = 11 * 11 = 121. Степень, присущая числу, может быть отрицательной, рациональной, десятичной, вещественной и даже комплексной. Фактически получается, что для того, чтобы посчитать степень числа, его нужно умножить на себя столько раз, сколько указано в степенном показателе.
Правило возведения дроби
В основе правила возведения дроби в степень лежит её определение с дробным показателем. Согласно ему, для решения задачи нужно отдельно возвести сначала числитель выражения, а затем знаменатель, не меняя занимаемые ими позиции. Например, дробь три шестых во второй степени будет равна: (3/6) 2 = 9/36. Используя свойства сокращения дробей, числитель и знаменатель можно разделить на девять. В итоге получится равенство: (3/6) 2 = 1/4.
Доказать это правило можно выполнив элементарные алгебраические действия. Для рассмотренного примера, согласно правилу арифметики, сначала необходимо выполнить деление, а после возведение в степень. Так, три разделить на шесть будет равно: 3/6 = 1/2 = 0,5. Затем полученное число следует возвести в квадрат: 0,5 2 = 0,5 * 0,5 = 0,25. Найденный ответ можно переписать в виде дроби 1/4, которая при сравнении полностью совпадает с ранее вычисленной.
Чтобы убедиться в истинности правила, можно и тут выполнить проверку. Дробь три разделить на пять в степени три можно решить, выполнив сначала деление, а после полученное число возвести в кубическую степень: (11 / 14) 3 = (0,78) 3 = 0,78 * 0,78 * 0,78 = 0,485. Ответ идентичен предыдущему, что и следовало доказать.
Таким образом, алгоритм возведения будет следующим:
Если показатель степени небольшой, то возведение можно выполнить просто умножив дробь на саму себя необходимое число раз. Например, (2/32) 3 = (2/32) * (2/32) *(2/32) = 1/4096. Алгоритм обыкновенного расчёта обычно не вызывает трудности, но часто приходиться иметь дело не только с обыкновенными дробями. При этом степень может быть даже отрицательной.
Но в любом случае нужно помнить, что если верхнюю и нижнюю часть дроби умножить или разделить на одно и то же число, то количественный показатель полученного выражения не изменится. Это важно, так как при возведении приходится часто выполнять преобразования.
Нулевая и отрицательная степень
При вычислении дроби, в показателе которой стоит ноль, исходят из свойств частного степеней с одинаковым основанием.
Ответ на 0 0 может быть любым. Поэтому для избежания путаницы считают, что решение записи 0 0 не имеет смысла, так же как и деление на ноль. Например, (12 / 34) 0 = 12 0 / 34 0 = 1 / 1 = 1 или (-3 / 4) 0 = 1, а вот для (0 / 23) 0 ответ будет не определён.
Рациональный показатель
В состав рациональных чисел входят все целые и дробные значения. По сути, ими называют значения, которые можно представить в виде обыкновенной или отрицательной дроби, как цифру ноль. При этом в числителе находится целое число, а в знаменателе – натуральное. Для того чтобы определить степень, нужно выяснить, что же представляет собой число с показателем в дробной форме.
Примеры решения
Для того чтобы понять и усвоить теорию, нужно попрактиковаться. Начинать необходимо с простых заданий, постепенно переходя к более сложным примерам. Возвести дробь в степень можно и на онлайн-калькуляторах, но желательно уметь выполнять это действие самостоятельно. Из наиболее типичных примеров, охватывающих все возможные ситуации, можно выделить следующие:
Отрицательная степень
Прежде чем перейти к изучению определения «отрицательная степень» рекомендуем повторно прочитать урок «Степень» и «Свойства степеней».
Необходимо уверенно понимать, что такое положительная степень числа и уверенно использовать её свойства в решении примеров.
Как возвести число в отрицательную степень
Чтобы возвести число в отрицательную степень нужно:
Общая формула возведения в отрицательную степень выглядит следующим образом.
Примеры возведения в отрицательную степень.
Любое число в нулевой степени — единица.
Примеры возведения в нулевую степень.
Как найти 10 в минус 1 степени
В уроке 8 класса «Стандартный вид числа» мы уже сталкивались с записью:
Теперь, зная определение отрицательной степени, давайте разберемся, почему « 10 » в минус первой степени равно « 0,1 ».
Возведем « 10 −1 » по правилам отрицательной степени. Перевернем « 10 » и запишем её в виде дроби «
| 1 |
| 10 |
» и заменим отрицательную степень « −1 » на
положительную степень « 1 ».
Возведем « 10 » в « 1 » степень. Помним, что любое число в первой степени равно самому числу.
Теперь по определению десятичной дроби запишем обыкновенную дробь в виде десятичной.
По такому же принципу можно найти « 10 » в минус второй, третьей и т.д.
Для упрощения перевода « 10 » в минус первую, вторую и т.д степени, нужно запомнить правило:
«Количество нулей после запятой равно положительному значению степени минус один ».
Проверим правило выше для « 10 −2 ».
Т.к. у нас степень « −2 », значит, будет всего один ноль (положительное значение степени « 2 − 1 = 1 ». Сразу после запятой ставим один ноль и за ним « 1 ».
Т.к. у нас степень « −1 », значит, нулей после запятой не будет (положительное значение степени « 1 − 1 = 0 ». Сразу после запятой ставим « 1 ».
То же самое правило работает и для « 10 −12 ». При переводе в десятичную дробь будет « 12 − 1 = 11 » нулей и « 1 » в конце.
Как возвести в отрицательную степень дробь
Чтобы возвести дробь в отрицательную степень нужно:
Пример. Требуется возвести в отрицательную степень дробь.
Перевернем дробь «
| 10 |
| 3 |
» и заменим отрицательную степень « −3 » на положительную « 3 ».
Возведем дробь в положительную степень по правилу возведения дроби в положительную степень. Т.е. возведем и числитель « 3 », и знаменатель « 10 » в третью степень.
(
| 10 |
| 3 |
) −3 = (
| 3 |
| 10 |
) 3 =
| 3 3 |
| 10 3 |
=
| 27 |
| 1000 |
Для более грамотного ответа запишем полученный результат в виде десятичной дроби.
(
| 10 |
| 3 |
) −3 = (
| 3 |
| 10 |
) 3 =
| 3 3 |
| 10 3 |
=
| 27 |
| 1000 |
= 0,027
Как возвести отрицательное число в отрицательную степень
Как и при возведении отрицательного числа в положительную степень, в первую очередь необходимо определить конечный знак результата возведения в степень. Вспомним основные правила еще раз.
Перевернем число « −5 » и заменим отрицательную степень « −2 »
на положительную « 2 ».
Далее откроем скобки и возведем во вторую степень и числитель « 1 »,
и знаменатель « 5 ».
Как возвести отрицательную дробь в отрицательную степень
Конечный знак результата возведения в степень отрицательной дроби определяется по тем же правилам, что и для целого отрицательного числа.
Разберемся на примере. Задание: возвести отрицательную дробь « (−
| 2 |
| 3 |
) » в « −3 » степень.
По правилу возведения дроби в отрицательную степень перевернем дробь и заменим отрицательную степень « −3 » на положительную « 3 ».
Теперь определим конечный знак результата возведения в « 3 » степень.
Нам остается только раскрыть скобки и возвести в степень и числитель « 3 », и знаменатель « 2 » в третью степень.
Для окончательного ответа выделим целую часть из дроби.
Рассмотрим другой пример возведения отрицательной дроби в отрицательную степень.
(−
| 9 |
| 11 |
) −2 = (−
| 11 |
| 9 |
) 2 =
| 11 2 |
| 9 2 |
=
| 121 |
| 81 |
= 1
| 40 |
| 81 |
Свойства отрицательной степени
Все свойства степени, которые используются для положительной степени, точно также применяются и для отрицательной степени.
В этом уроке мы не будем повторно подробно разбирать каждое свойство степени, но еще раз приведем основные формулы свойств степени и покажем примеры их использования.
Примеры решений заданий с отрицательной
степенью
Колягин 9 класс. Задание № 1
Представить в виде степени.
Колягин 9 класс. Задание № 5
Записать в виде степени с отрицательным числом.
Свойства степеней и действия с ними
Зачем нужны степени? Где они тебе пригодятся? Почему тебе нужно тратить время на их изучение?
Как обычно — чтобы облегчить себе жизнь. Знание свойств степеней позволит тебе упрощать вычисления и считать быстрее, что пригодится и в жизни и на ОГЭ или ЕГЭ!
Чтобы узнать все о степенях и научиться пользоваться свойствами степеней, читай эту статью.
P.S Если ты хорошо знаешь степени и тебе надо только повторить, переходи сразу к продвинутому уровню.
НАЧАЛЬНЫЙ УРОВЕНЬ
Степени. Коротко о главном
Определение степени:
Свойства степеней:
| Произведение степеней с одинаковым основанием: | \( <^ |
| Произведение степеней с одинаковыми показателями: | \( <^ |
| Деление степеней с одинаковым основанием: | \( \frac<<^ |
| Деление степеней с одинаковыми показателями: | \( \frac<<^ |
| Возведение степени в степень: | \( <<\left( <^ |
| Дробная степень: | \( <^<\frac |
Особенности степеней:
Возведение в степень – это такая же математическая операция, как сложение, вычитание, умножение или деление.
Сейчас объясню все человеческим языком на очень простых примерах. Будь внимателен. Примеры элементарные, но объясняющий важные вещи. Начнем со сложения.
Сложение
Объяснять тут нечего. Ты и так все знаешь: нас восемь человек. У каждого по две бутылки колы. Сколько всего колы? Правильно – 16 бутылок. Теперь умножение.
Умножение
Тот же самый пример с колой можно записать по-другому: \(\displaystyle 2\cdot 8=16\).
Математики — люди хитрые и ленивые. Они сначала замечают какие-то закономерности, а потом придумывают способ как быстрее их «считать».
В нашем случае они заметили, что у каждого из восьми человек одинаковое количество бутылок колы и придумали прием, который называется умножением.
Согласись, \(\displaystyle 2\cdot 8=16\) считается легче и быстрее, чем \(\displaystyle 2+2+2+2+2+2+2+2=16\).
И еще одна важная деталь. Ошибок при таком счете делается гораздо меньше. Математики из Стэнфорда, кстати, считают, что человек, знающий приемы счета, делает это в два раза легче и быстрее и совершает в два раза меньше ошибок. Работы меньше, а результат лучше.
Итак, чтобы считать быстрее, легче и без ошибок, нужно всего лишь запомнить таблицу умножения. Ты, конечно, можешь делать все медленнее, труднее и с ошибками, но лучше ее запомнить! Вот таблица умножения. Выучи ее наизусть.
И другая таблица, красивее:
А какие еще хитрые приемы счета придумали ленивые математики? Правильно – возведение числа в степень.
Возведение числа в степень
Если тебе нужно умножить число само на себя пять раз, то математики говорят, что тебе нужно возвести это число в пятую степень.
Например, \(\displaystyle 2\cdot 2\cdot 2\cdot 2\cdot 2=<<2>^<5>>\). Математики помнят, что два в пятой степени – это \(\displaystyle 32\).
И решают такие задачки в уме – быстрее, легче и без ошибок.
Для этого нужно всего лишь запомнить то, что выделено цветом в таблице степеней чисел. Поверь, это сильно облегчит тебе жизнь.
Кстати, почему вторую степень называют квадратом числа, а третью — кубом? Что это значит? Очень хороший вопрос. Сейчас будут тебе и квадраты, и кубы.
Примеры из жизни
Начнем с квадрата или со второй степени числа.
Представь себе квадратный бассейн размером \( \displaystyle 3\) метра на \( \displaystyle 3\) метра. Бассейн стоит у тебя на даче. Жара и очень хочется купаться.
Но… бассейн без дна! Нужно застелить дно бассейна плиткой. Сколько тебе надо плитки? Для того чтобы это определить, тебе нужно узнать площадь дна бассейна.
Ты можешь просто посчитать, тыкая пальцем, что дно бассейна состоит из \( \displaystyle 9\) кубиков метр на метр. Если у тебя плитка метр на метр, тебе нужно будет \( \displaystyle 9\) кусков. Это легко…
Но где ты видел такую плитку? Плитка скорее будет \( \displaystyle 10\) см на \( \displaystyle 10\) см. И тогда «пальцем считать» замучаешься. Тогда придется умножать.
Итак, по одной стороне дна бассейна у нас поместится \( \displaystyle 30\) плиток (\( \displaystyle \frac<300\ см><10\ см>=30\) штук) и по другой тоже \( \displaystyle 30\) плиток.
Ты заметил, что для определения площади дна бассейна мы умножили одно и то же число само на себя? Что это значит? Раз умножается одно и то же число, мы можем воспользоваться приемом «возведение в степень».
Конечно, когда у тебя всего два числа, все равно перемножить их или возвести в степень. Но если у тебя их много, то возводить в степень значительно проще и ошибок при расчетах получается тоже меньше.
Иными словами, вторую степень числа всегда можно представить в виде квадрата. И наоборот, если ты видишь квадрат – это ВСЕГДА вторая степень какого-то числа.
Квадрат – это изображение второй степени числа.
Теперь куб или третья степень числа. Тот же самый бассейн. Но теперь тебе нужно узнать, сколько воды придется залить в этот бассейн. Тебе нужно посчитать объем. (Объемы и жидкости, кстати, измеряются в кубических метрах. Неожиданно, правда?)
Нарисуй бассейн: дно размером \( \displaystyle 3\) на \( \displaystyle 3\) метра и глубиной \( \displaystyle 3\) метра и попробуй посчитать, сколько всего кубов размером метр на метр войдет в твой бассейн.
Прямо показывай пальцем и считай! Раз, два, три, четыре…двадцать два, двадцать три… Сколько получилось? Не сбился? Трудно пальцем считать?
Так-то! Бери пример с математиков. Они ленивы, поэтому заметили, что чтобы посчитать объем бассейна, надо перемножить друг на друга его длину, ширину и высоту.
В нашем случае объем бассейна будет равен \( \displaystyle 3\cdot 3\cdot 3=27\) кубов… Легче правда?
А теперь представь, насколько математики ленивы и хитры, если они и это упростили. Свели все к одному действию. Они заметили, что длина, ширина и высота равна и что одно и то же число перемножается само на себя…
Остается только запомнить таблицу степеней. Если ты, конечно, такой же ленивый и хитрый как математики. Если любишь много работать и делать ошибки – можешь продолжать считать пальцем.
Ну и чтобы окончательно убедить тебя, что степени придумали лодыри и хитрюги для решения своих жизненных проблем, а не для того чтобы создать тебе проблемы, вот тебе еще пара примеров из жизни.
У тебя есть \( \displaystyle 2\) миллиона рублей. В начале каждого года ты зарабатываешь на каждом миллионе еще один миллион. То есть каждый твой миллион в начале каждого года удваивается. Сколько денег у тебя будет через \( \displaystyle 5\) лет?
Если ты сейчас сидишь и «считаешь пальцем», значит ты очень трудолюбивый человек и.. глупый. Но скорее всего ты дашь ответ через пару секунд, потому что ты – умный! Итак, в первый год — два умножить на два… во второй год — то, что получилось, еще на два, в третий год… Стоп!
Ты заметил, что число \( \displaystyle 2\) перемножается само на себя \( \displaystyle 6\) раз. Значит, два в шестой степени – \( \displaystyle 64\) миллиона! А теперь представь, что у вас соревнование и эти \( \displaystyle 64\) миллиона получит тот, кто быстрее посчитает…
Стоит запомнить степени чисел, как считаешь?
У тебя есть \( \displaystyle 1\) миллион. В начале каждого года ты зарабатываешь на каждом миллионе еще два. Здорово правда? Каждый миллион утраивается. Сколько денег у тебя будет через \( \displaystyle 4\) года?
Уже скучно, потому что ты уже все понял: три умножается само на себя \( \displaystyle 4\) раза.
Теперь ты знаешь, что с помощью возведения числа в степень ты здорово облегчишь себе жизнь. Давай дальше посмотрим на то, что можно делать со степенями и что тебе нужно знать о них.