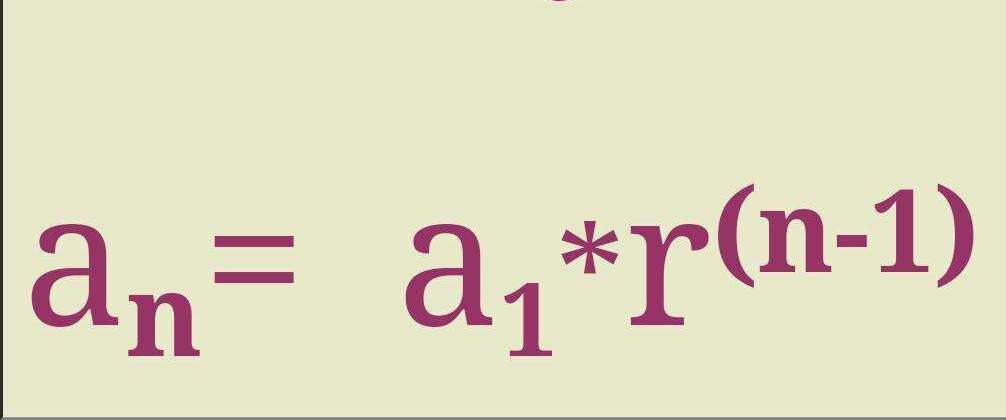Две бесконечно убывающие геометрические прогрессии таковы что первый
Две бесконечно убывающие геометрические прогрессии таковы что первый
Бесконечно убывающая геометрическая прогрессия.
659.Для доказательства того, что данные числа образуют геометрическую убывающую прогрессию, надо проверить, будут ли равны отношения 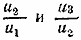
Так как 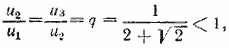
660. Как в предыдущей задаче, находим, что выражение в квадратных скобках равно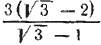
Учитывая, что u1 = 4, получаем биквадратное уравнение 81q 4 —81q 2 + 8 = 0; его корни: 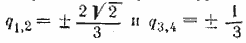
Отв. S‘ = 12 (3 + 2√ 2 ) и S» = 6.
Разделив (1) на (2), получим уравнение
Деля 2) на 1)-, получим: q = 1 /3, а из первого уравнения находим u1 =32.
С другой стороны, сумма всех членов прогрессии есть 12+36=48 По формуле суммы бесконечно убывающей прогрессии имеем 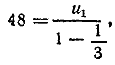
Деля (2) на (1), находим
Исключая u1 из уравнений (1) и (3), получаем
665. Задача решается аналогично предыдущей. Для определении u1 и q получим систему уравнений:
После исключения из этих уравнений u1 получим уравнение
3q 2 —10q +3=0. Из двух корней его годится только q = 1 /3 (другой q = 3 больше единицы). Из уравнения (1) находим u1= 2.
666. Задача решается аналогично задачам 664, 665. Для определения u1 и q получим систему уравнений:
Из двух его корней q1= — 3 /2, q2= 1 /2 годится только второй, так как абсолютная величина первого больше единицы. Из (1) находим u1= 12.
Дидактические материалы по алгебре, 10-11 класс, Зив Б.Г., Гольдич В.А., 2013
Дидактические материалы по алгебре, 10-11 класс, Зив Б.Г., Гольдич В.А., 2013.
Данное пособие содержит самостоятельные и контрольные работы по курсу «Алгебра и начала анализа» для 10-11 классов, составленные в полном соответствии со школьной программой. Пособие может быть использовано как в обычных школах, так и в математических гимназиях и лицеях.
Примеры.
Произведение первого, третьего и пятого членов бесконечно убывающей геометрической прогрессии равно (—8), а сумма второго и четвертого равна 5. Найдите сумму этой прогрессии.
Две бесконечно убывающие геометрические прогрессии таковы, что первый член первой прогрессии является знаменателем второй, а знаменатель первой является первым членом второй прогрессии. Сумма всех членов прогрессий равна 2. Найдите первый член первой прогрессии, если ее знаменатель равен 1\3
Найдите знаменатель бесконечно убывающей геометрической прогрессии, у которой каждый ее член относится к сумме всех последующих членов, как 7 к 9.
Содержание
Предисловие
10-й класс. Самостоятельные работы
1. Действительные числа
2. Бесконечно убывающая геометрическая прогрессия. Арифметический корень натуральной степени
3. Степень с действительным показателем
4. Степенная функция и обратная функция
5. Равносильность уравнений и неравенств
6. Иррациональные уравнения
7. Иррациональные неравенства
8. Показательные уравнения и неравенства
9. Системы показательных уравнений и неравенств
10. Свойства логарифмов
11. Логарифмические уравнения и системы
12. Логарифмические неравенства
13. Определение тригонометрических функций
14. Тригонометрические тождества
15. Формулы сложения. Двойные углы
16. Формулы приведения. Преобразование суммы в произведение
17. Простейшие тригонометрические уравнения
18. Тригонометрические уравнения
19. Тригонометрические системы и неравенства
20. Свойства тригонометрических функций
21. Графики тригонометрических функций
22. Обратные тригонометрические функции
10-й класс. Контрольные работы
1. Действительные числа
2. Степенная функция
3. Показательная функция
4. Логарифмическая функция
5. Тригонометрические формулы
6. Тригонометрические уравнения
7. Тригонометрические функции
8. Итоговая контрольная работа
11-й класс. Самостоятельные работы
1. Производная
2. Производная степенной функции. Правила дифференцирования. Производная сложной функции
3. Геометрический смысл производной
4. Производные некоторых элементарных функций
5. Исследование функции на монотонность и экстремум
6. Графики функций
7. Наибольшее и наименьшее значение функции
8. Первообразные
9*. Интеграл
11-й класс. Проверочные работы на повторение
1. Рациональные уравнения и неравенства
2. Иррациональные уравнения и неравенства
3. Показательные и логарифмические уравнения и неравенства
4. Тригонометрия
11-й класс. Контрольные работы
1. Производная и ее геометрический смысл
2. Исследование функции с помощью производной
3. Первообразные и интеграл
4. Контрольная работа №1 на повторение пройденного материала
5. Контрольная работа №2 на повторение пройденного материала
6. Контрольные тесты
10-й класс. Ответы к самостоятельным работам
10-й класс. Ответы к контрольным работам
11-й класс. Ответы к самостоятельным работам
11-й класс. Ответы к проверочным работам на повторение
11-й класс. Ответы к контрольным работам.
Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России. Купить эту книгу
Две бесконечно убывающие геометрические прогрессии таковы что первый
Бесконечная геометрическая прогрессия b1, b2. bn. состоит из различных натуральных чисел. Пусть
Пусть S1 = b1 и Sn = b1 + b2 +. + bn при всех натуральных
а) Приведите пример такой прогрессии, для которой среди чисел S1, S2, S3, S4 ровно два числа делятся на 24.
б) Существует ли такая прогрессия, для которой среди чисел S1, S2, S3, S4 ровно три числа делятся на 24.
в) Какое наибольшее количество чисел среди S1, S2. S8 может делиться на 24, если известно, что S1 на 24 не делится?
а) например Только
и
кратны 24.
в) Продолжая прогрессию из п. а), получим пример для четырех чисел. Попробуем доказать, что больше сделать нельзя. Допустим, таких сумм минимум пять. Тогда среди них есть две с соседними номерами, Значит, их разность — один из членов прогрессии — делится на 24.
Рассмотрим, как устроены все члены прогрессии, кратные трем. Степень тройки во всех членах прогрессии растет при увеличении номера на одну и ту же величину, или убывает на одну и ту же величину (для бесконечной прогрессии это на самом деле невозможно), или остается неизменной. Значит, либо ни один из членов прогрессии не кратен трем (а тогда и ), либо трем кратны все члены прогрессии, кроме может быть первого или последнего. Если все, кроме первого — ни одна из сумм не будет кратна трем. Если все, кроме последнего — умножим все члены прогрессии на 3, от этого суммы не перестанут делиться на 24, первый член не начнет делиться на 24 (он и так был кратен трем). Итак, можно считать, что все члены прогрессии кратны трем. Тогда поделим их все на 3 и будем изучать делимость
на 8.
Рассуждая аналогично про делимость на степени двойки, придем либо к ответу либо к возможности сократить все на
и изучению делимости на
Затем — к изучению делимости на
Для нее уже вариантов, дающих больше четырех сумм, не останется — либо все члены прогрессии имеют одинаковую четность (и Значит, нечетны и там 4 суммы), либо все четны, кроме первого (тогда четных сумм нет).
Ответ: а) 12, 36, 108, 324; б) нет; в) 4.
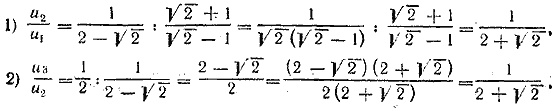
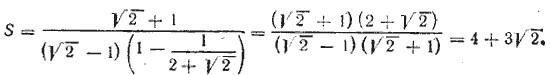
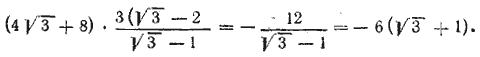
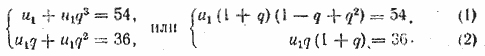
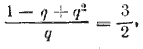
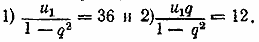
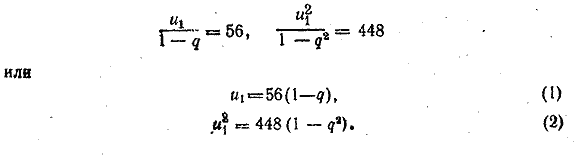

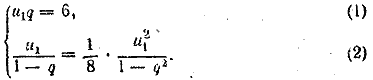



 найдите пятый член.
найдите пятый член. 

 образующих геометрическую прогрессию со знаменателем
образующих геометрическую прогрессию со знаменателем  .
.


 . И, опять, если n неограниченно возрастает, то площадь, как угодно близко приближается к нулю.
. И, опять, если n неограниченно возрастает, то площадь, как угодно близко приближается к нулю.
 при
при  .
.
 .
. ;
;  .
. ;
;  ;
;  ;
;  .
. данная последовательность не является бесконечно убывающей геометрической прогрессией.
данная последовательность не является бесконечно убывающей геометрической прогрессией.



 .
.
 . Поэтому
. Поэтому  , т.е.
, т.е.  .
. ,
,
 Так как
Так как 
 .
.




 Вам будет интересно: Future in the Past: правила речи, склонение, время, понятие, определения, особенности изучения и нюансы произношения
Вам будет интересно: Future in the Past: правила речи, склонение, время, понятие, определения, особенности изучения и нюансы произношения