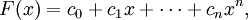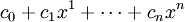Двучлен в математике что это
Значение слова «двучлен»
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
ДВУЧЛЕ’Н, а, м. (мат.). Алгебраическое выражение, представляющее сумму или разность двух одночленов; то же, что бином.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
двучле́н
1. матем. алгебраическая сумма двух одночленов
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: укомплектование — это что-то нейтральное, положительное или отрицательное?
Синонимы к слову «двучлен»
Предложения со словом «двучлен»
Понятия, связанные со словом «двучлен»
Отправить комментарий
Дополнительно
Предложения со словом «двучлен»
За каждым из таких двучленов стоит большее или меньшее количество языковых единиц – носителей соответствующих значений, а все вместе они охватывают значительную часть русской лексики, объединяющую слова, принадлежащие к различным лексическим и тематическим группам, к различным семантическим полям и представляющие все основные части речи.
Здесь ключ к структуре понятия «суверенитет»: оно предстаёт нам как семантический двучлен, где факт власти выступает вместе с её внешним признанием.
На тех, кто не умел решать задачи про трубы в бассейне или не знал алгебраических формул умножения двучлена, она смотрела со снисходительным сожалением.
Двучлен
где ci фиксированные коэффициенты, а x — переменная. Многочлены составляют один из важнейших классов элементарных функций.
Изучение полиномиальных уравнений и их решений составляло едва ли не главный объект «классической алгебры». С изучением многочленов связан целый ряд преобразований в математике: введение в рассмотрение нуля, отрицательных, а затем и комплексных чисел, а также появление теории групп как раздела математики и выделение классов специальных функций в анализе.
Техническая простота вычислений, связанных с многочленами, по сравнению с более сложными классами функций, а также тот факт, что множество многочленов плотно в пространстве непрерывных функций на компактных подмножествах евклидова пространства (смотри аппроксимационная теорема Вейерштрасса), способствовали развитию методов разложения в ряды и полиномиальной интерполяции в математическом анализе.
Многочлены также играют ключевую роль в алгебраической геометрии, объектом которой являются множества, определённые как решения систем многочленов. Особые свойства преобразования коэффициентов при умножении многочленов используются в алгебраической геометрии, алгебре, теории узлов и других разделах математики для кодирования, или выражения многочленами свойств различных объектов.
Содержание
Определение
Многочлен (или полином) от n переменных — есть конечная формальная сумма вида
,
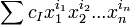
где I = (i1,i2. in) есть набор из целых неотрицательных чисел (называется мультииндекс), cI — число (называемое «коэффициент многочлена»), зависящее только от мультииндекса I.
В частности, многочлен от одной переменной есть конечная формальная сумма вида
Коэффициенты многочлена обычно берутся из определённого коммутативного кольца R (чаще всего поля, например, поля вещественных или комплексных чисел). В этом случае, относительно операций сложения и умножения многочлены образуют кольцо (более того ассоциативно-коммутативную алгебру над кольцом R без делителей нуля) которое обозначается
Связанные определения
Делимость
Например, многочлен x 4 + 2, неприводимый в поле рациональных чисел, разлагается на два множителя в поле вещественных чисел и на четыре множителя в поле комплексных чисел.
Вообще, каждый многочлен от одного переменного x разлагается в поле вещественных чисел на множители первой и второй степени, в поле комплексных чисел — на множители первой степени (основная теорема алгебры).
Для двух и большего числа переменных этого уже нельзя утверждать. Над любым полем для любого n > 2 существуют многочлен от n переменных, неприводимые в любом расширении этого поля. Такие многочлены называются абсолютно неприводимыми.
Полиномиальные функции
.
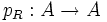
В случае если R есть поле вещественных или комплексных чисел (а также любое другое поле с бесконечным числом элементов) то функция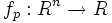 
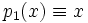
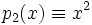
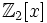
полностью определяет многочлен p. Однако в общем случае это неверно, например: многочлены 
и 
из 
определяют тождественно равные функции 
.
Двучлен
Смотреть что такое «Двучлен» в других словарях:
двучлен — двучлен … Орфографический словарь-справочник
двучлен — бином Словарь русских синонимов. двучлен сущ. • бином Словарь русских синонимов. Контекст 5.0 Информатик. 2012. двучлен … Словарь синонимов
ДВУЧЛЕН — (бином) алгебраическая сумма 2 одночленов … Большой Энциклопедический словарь
ДВУЧЛЕН — ДВУЧЛЕН, двучлена, муж. (мат.). Алгебраическое выражение, представляющее сумму или разность двух одночленов; то же, что бином. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
ДВУЧЛЕН — ДВУЧЛЕН, а, муж. (спец.). Алгебраическое выражение многочлен, состоящий из двух одночленов. | прил. двучленный, ая, ое. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
двучлен — бином двучленный биномиальный — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы биномдвучленныйбиномиальный EN binomial … Справочник технического переводчика
двучлен — а; м. Матем. Алгебраическое выражение, представляющее сумму или разность двух одночленов; бином. ◁ Двучленный, ая, ое. Д ое уравнение. * * * двучлен (бином), алгебраическая сумма 2 одночленов. * * * ДВУЧЛЕН ДВУЧЛЕН (бином), алгебраическая сумма 2 … Энциклопедический словарь
Двучлен — (мат.) В добавление сказанного в ст. Бином (см.) заметим по поводу бинома Ньютона. Уже Вьетту было известно, что от возвышения Д. а + b в какую угодно целую положительную степень n получается формула вида (1) (а +b)n = аn + P1an 1b1 + P2an 2b2 + … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Двучлен — м. Алгебраическое выражение, представляющее собою сумму или разность двух одночленов; бином (в математике). Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
двучлен — двучлен, двучлены, двучлена, двучленов, двучлену, двучленам, двучлен, двучлены, двучленом, двучленами, двучлене, двучленах (Источник: «Полная акцентуированная парадигма по А. А. Зализняку») … Формы слов
Многочлен стандартного вида
Определение многочлена
Многочлен — это сумма одночленов. Получается, что многочлен — не что иное, как несколько одночленов, собранных «под одной крышей».
Одночлен — это частный случай многочлена.
Рассмотрим примеры многочленов:
Если многочлен состоит из двух одночленов, его называют двучленом:
Многочлен — это сумма одночленов, поэтому знак «минус» относится к числовому коэффициенту одночлена. Именно поэтому мы записываем – 3×2, а не просто 3×2.
Этот же многочлен можно записать вот так:
Это значит, что каждый одночлен важно рассматривать вместе со знаком, который перед ним стоит.
Многочлен вида 10x – 3×2 + 7 называется трехчленом.
Линейный двучлен — это многочлен первой степени: ax + b. a и b здесь — некоторые числа, x — переменная.
Если разделить многочлен с переменной x на линейный двучлен x – b (где b — некоторое положительное или отрицательное число) — остаток будет только многочленом нулевой степени. То есть некоторым числом N, которое можно определить без поиска частного.
Если многочлен содержит обычное число — это число является свободным членом многочлена.
Свободный член многочлена не имеет буквенной части. Кроме того, любое числовое выражение — это многочлен. Например, вот такие числовые выражения — тоже многочлены:
Такие выражения состоят из свободных членов.
Многочлен стандартного вида
Недостаточно просто знать, что такое многочлен и что такое одночлен. Это целая алгебраическая экосистема, где у всего есть названия, определения и особенности.
Давайте разберемся, что такое многочлен стандартного вида. Многочленом стандартного вида называют многочлен, каждый член которого имеет одночлен стандартного вида и не содержит подобных членов.
Получается, что всякий многочлен можно привести к стандартному виду. Таким образом можно получить многочлен, работать с которым гораздо проще и приятнее.
К стандартному виду многочлен приводится очень просто. Нужно лишь привести в нем подобные слагаемые.
Подобные слагаемые — это подобные члены многочлена. Приведение подобных слагаемых в многочлене — приведение его подобных членов. Тут же возникает резонный вопрос: Что такое подобные члены многочлена? Это члены с одинаковой буквенной частью.
Давайте разберем на примере, как «нестандартный» многочлен приводится к стандартному виду.
Дан красавец многочлен: 3x + 5xy2 + x – xy2
Приведем подобные слагаемые. Для этого найдем все члены с одинаковыми буквенными составляющими:
Как видите, в получившемся многочлене нет подобных членов. Такой многочлен — это многочлен стандартного вида.
Степень многочлена
Многочлен может иметь степень — имеет на это полное право.
Степень многочлена стандартного вида — это наибольшая из степеней, входящих в него одночленов.
Из определения можно сделать вывод, что степень многочлена возможно определить только после приведения его к стандартному виду.
Рассмотрим на примере:
Дан многочлен 6x + 4xy2 + x + xy2
Сначала приводим многочлен к стандартному виду — для этого приводим подобные слагаемые:
Получаем многочлен стандартного вида 6x + 4xy2 + x + xy2 = 7x + 5xy2.
Отсюда делаем вывод, что многочлен 7x + 5xy2 — многочлен второй степени.
Кроме того, можно сделать вывод, что и исходный многочлен 6x + 4xy2 + x + xy2 — многочлен второй степени, поскольку оба многочлена равны друг другу.
В некоторых случаях необходимо сначала привести к стандартному виду одночлены многочлена, а затем уже и сам многочлен.
Пример:
Получившийся многочлен без труда приводим к стандартному виду. Приводим подобные слагаемые:
Коэффициенты многочлена
Коэффициенты членов многочлена — это числа, которые указаны перед переменными множителями. Если перед переменной нет числа, то коэффициент этого члена = 1.
Иными словами — коэффициенты членов многочлена — это члены многочлена, представленные в виде стандартных одночленов.
Например:
Все одночлены имеют стандартный вид. 2, 5 и 18 — коэффициенты членов данного многочлена.
Кажется, со стандартным видом многочлена все понятно. Чтобы без труда приводить любой многочлен к стандартному виду, нужно потренироваться, ведь в 7 классе только и разговоров, что о многочленах. Давайте разберем несколько примеров. Попробуйте решить их самостоятельно, сверяясь с ответами.
Задание раз. Приведите многочлен к стандартному виду и определите его степень: 4x + 6xy2 + x – xy2.
Как решаем: приведем подобные слагаемые. Для этого найдем все члены с одинаковыми буквенными составляющими:
Получаем многочлен стандартного вида: 4x + 6xy2 + x – xy2 = 5x + 5xy2.
Ответ: стандартный вид многочлена 5x + 5xy2. Данный многочлен — многочлен второй степени.
Многочлен приведен к стандартному виду.
Как решаем: приведем подобные слагаемые. Для этого найдем все члены с одинаковыми буквенными составляющими:
Разобраться в многочленах не так-то просто. В этой теме немало нюансов и подводных камней. Чтобы не запутаться в множестве похожих одно на другое определений, побольше практикуйтесь. Чтобы перейти на следующую ступень и начать выполнение арифметических действий с многочленами, важно научиться приводить многочлен к стандартному виду.
Умножение многочлена на многочлен
Определение многочлена
Прежде чем мы расскажем, как умножить один многочлен на другой многочлен, разберемся в основных понятиях.
Одночлен — это произведение чисел, переменных и степеней.
Многочлен— алгебраическое выражение, которое представляет из себя сумму или разность нескольких одночленов.
Стандартный вид многочлена — представление многочлена в виде суммы одночленов стандартного вида, среди которых нет подобных одночленов.
Как привести многочлен к стандартному виду:
Вспомним, как умножать многочлен на одночлен, двучлен на двучлен, трехчлен на трехчлен:
(a + b) * (c + d) = ac + ad + bc + bd.
(a + b + c) * (x + y) = ax + bx + cx + ay + by + cy.
(a + b + c) 2 = a 2 + b 2 + c 2 + 2ab + 2ac + 2bc.
Эти правила можно описать так: чтобы умножить один многочлен на другой, нужно каждый член первого умножить на каждый член второго многочлена. Затем полученные произведения сложить и привести результат к многочлену стандартного вида, если это возможно.
Правило умножения многочлена на многочлен
Рассмотрим пример, а после решения сформулируем правило умножения многочлена на многочлен:
Правило умножения многочлена на многочлен
Чтобы умножить многочлен на многочлен, надо каждый член первого многочлена умножить на каждый член второго многочлена и все полученные произведения сложить.
Алгоритм умножения многочлена на многочлен:
Рассмотрим пример умножения многочлена на многочлен:
(6x – 2a) * (4 – 3x).
Ответ: (6x – 2a) * (4 – 3x) = 24x – 18x 2 – 8a + 6ax.
Рассмотрим пример умножения трех многочленов:
(x – 2) * (3x + 1) * (4x – 3).
Ответ: (x – 2) * (3x + 1) * (4x – 3) = 12x 3 – 29x 2 + 7x + 6.
Теперь мы знаем все из темы умножения многочлена на многочлен. Осталось отточить на практике новый навык и ловить хорошие и отличные отметки на контрольных.
Примеры умножения многочлена на многочлен
Рассмотрим еще несколько примеров, чтобы закрепить пройденный материал.
Пример 1. Выполнить умножение многочленов:
2 − 3x и x 2 − 7x + 1.
Запишем произведение: (2 − 3x)(x 2 − 7x + 1).
Из полученных выражений составим сумму: 2x 2 + 2(−7x) + 2*1 − 3xx 2 − 3x(−7x) − 3x*1.
Чтобы убедиться, что мы все сделали правильно, посчитаем количество членов в полученной сумме. Их шесть. Так и должно быть, так как исходные многочлены состоят из 2 и 3 членов: 2 * 3 = 6.
Осталось полученную сумму преобразовать в многочлен стандартного вида:
Пример 2. Найти произведение трех многочленов:
x 2 + xy − 1, x + y и 2y − 3.
Запишем их произведение: (x 2 + xy − 1)(x + y)(2y − 3).
Умножим первые два многочлена:
(x 2 + xy − 1)(x + y) = x 2 x + x 2 y + xyx + xyy − 1x − 1y = x 3 + 2x 2 y + xy 2 − x − y.
Таким образом: (x 2 + xy − 1)(x + y)(2y − 3) = (x 3 + 2x 2 y + xy 2 − x − y)(2y − 3).
Снова выполним умножение двух многочленов:
(x 3 + 2x 2 y + xy 2 − x − y)(2y − 3) = x 3 2y + x 3 (−3) + 2x 2 y 2 y + 2x 2 y(−3) + xy 2 2y + xy 2 (−3) − x 2 y − x(−3) − y 2 y − y(−3) = 2x 3 y − 3x 3 + 4x 2 y 2 − 6x 2 y + 2xy 3 − 3xy 2 − 2xy + 3x − 2y 2 + 3y.
Ответ: (x 2 + xy − 1)(x + y)(2y − 3) = 2x 3 y − 3x 3 + 4x 2 y 2 − 6x 2 y + 2xy 3 − 3xy 2 − 2xy + 3x − 2y 2 + 3y.