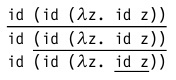E hc лямбда что это за формула

Лямбда-функции и замыкания

Конечно многие из нас знакомы с этим понятием, однако данная статья рассчитана на новичков. В данном посте постараюсь рассмотреть данный феномен и привести примеры использования. Для начала необходимо понять что же такое лямбда-функция. Итак, лямбда-функция, часто ее называют анонимной, т. е. функция при определении которой не нужно указывать ее имя. Возвращаемое значение такой функцией присваивается переменной, через которую в последствие эту функцию можно вызывать.
До выхода PHP 5.3 определять лямбда-функции было возможно, но их нельзя было назвать полноценными. Сейчас я приведу пару примеров и продолжим рассматривать данные понятия.

Конечно динамическое создание функций не решает всех проблем, однако порой написание такой одноразовой функции может быть полезным. Можно расширить наш пример:

Понятие замыкания наверняка знакомо программистам на JavaScript, а так же программистам на многих других языках. Замыкание — это функция, охватывающая или замыкающая текущую область видимости. Что бы понять все это, рассмотрим пример:

Как вы уже могли заметить, функция не имеет имени и результат присваивается переменной. Лямбда-функция, созданная таким образом, возвращает значение в виде объекта типа closure.
В PHP 5.3 стало возможно вызывать объекты как если бы они были функциями. А именно магический метод __invoke() вызывается каждый раз, когда класс вызывается как функция.
Переменные недоступны внутри функции, если они не объявлены глобальными, так же переменные из дочернего контекста недоступны если только не используется зарезервированное слово use. Обычно в PHP переменные передаются в замыкание значением, это поведение можно изменить с помощью ампермсанда перед переменной в выражении use. Рассмотрим пример:

Этот пример уже можно использовать для достаточно гибкого прототипирования. Достаточно объявить методы для всех SQL-операций с объектом.
Автор не призывает всех придерживаться такой практики, равно как и не считает что так лучше, все вышеописанное лишь пример использования, причем возможно не самый техничный и интересный, и не более того.
UPD Говоря о том самом длинном регулярном выражении, я не стал подписывать его в комментариях и решил вынести сюда. Оно лишь ищет строки в одинарных и двойных кавычках, а так же имена таблиц и экранирует их.

Источник

λ-исчисление. Часть первая: история и теория

Идею, короткий план и ссылки на основные источники для этой статьи мне подал хабраюзер z6Dabrata, за что ему огромнейшее спасибо.

UPD: в текст внесены некоторые изменения с целью сделать его более понятным. Смысловая составляющая осталась прежней.

Вступление

Возможно, у этой системы найдутся приложения не только
в роли логического исчисления. (Алонзо Чёрч, 1932)

Вообще говоря, лямбда-исчисление не относится к предметам, которые «должен знать каждый уважающий себя программист». Это такая теоретическая штука, изучение которой необходимо, когда вы собираетесь заняться исследованием систем типов или хотите создать свой функциональный язык программирования. Тем не менее, если у вас есть желание разобраться в том, что лежит в основе Haskell, ML и им подобных, «сдвинуть точку сборки» на написание кода или просто расширить свой кругозор, то прошу под кат.

Начнём мы с традиционного (но краткого) экскурса в историю. В 30-х годах прошлого века перед математиками встала так называемая проблема разрешения (Entscheidungsproblem), сформулированная Давидом Гильбертом. Суть её в том, что вот есть у нас некий формальный язык, на котором можно написать какое-либо утверждение. Существует ли алгоритм, за конечное число шагов определяющий его истинность или ложность? Ответ был найден двумя великими учёными того времени Алонзо Чёрчем и Аланом Тьюрингом. Они показали (первый — с помощью изобретённого им λ-исчисления, а второй — теории машины Тьюринга), что для арифметики такого алгоритма не существует в принципе, т.е. Entscheidungsproblem в общем случае неразрешима.

Так лямбда-исчисление впервые громко заявило о себе, но ещё пару десятков лет продолжало быть достоянием математической логики. Пока в середине 60-х Питер Ландин не отметил, что сложный язык программирования проще изучать, сформулировав его ядро в виде небольшого базового исчисления, выражающего самые существенные механизмы языка и дополненного набором удобных производных форм, поведение которых можно выразить путем перевода на язык базового исчисления. В качестве такой основы Ландин использовал лямбда-исчисление Чёрча. И всё заверте…

λ-исчисление: основные понятия

Синтаксис

В основе лямбда-исчисления лежит понятие, известное ныне каждому программисту, — анонимная функция. В нём нет встроенных констант, элементарных операторов, чисел, арифметических операций, условных выражений, циклов и т. п. — только функции, только хардкор. Потому что лямбда-исчисление — это не язык программирования, а формальный аппарат, способный определить в своих терминах любую языковую конструкцию или алгоритм. В этом смысле оно созвучно машине Тьюринга, только соответствует функциональной парадигме, а не императивной.

Мы с вами рассмотрим его наиболее простую форму: чистое нетипизированное лямбда-исчисление, и вот что конкретно будет в нашем распоряжении.

Процесс вычисления

Рассмотрим следующий терм-применение:

Существует несколько стратегий выбора редекса для очередного шага вычисления. Рассматривать их мы будем на примере следующего терма:

который для простоты можно переписать как

(напомним, что id — это функция тождества вида λx.x )

В этом терме содержится три редекса:

Недостатком стратегии вызова по значению является то, что она может зациклиться и не найти существующее нормальное значение терма. Рассмотрим для примера выражение

(λx.λy. x) z ((λx.x x)(λx.x x))

Этот терм имеет нормальную форму z несмотря на то, что его второй аргумент такой формой не обладает. На её-то вычислении и зависнет стратегия вызова по значению, в то время как стратегия вызова по имени начнёт с самого внешнего терма и там определит, что второй аргумент не нужен в принципе. Вывод: если у редекса есть нормальная форма, то «ленивая» стратегия её обязательно найдёт.

На этом закончим вводную в лямбда-исчисление. В следующей статье мы займёмся тем, ради чего всё и затевалось: программированием на λ-исчислении.

Источник

Лямбда-исчисление

А сегодня немного теории. Я не считаю, что лямбда-исчисление является необходимым знанием для любого программиста. Однако, если вам нравится докапываться до истоков, чтобы понять на чем основаны многие языки программирования, вы любознательны и стремитесь познать все в этом мире или просто хотите сдать экзамен по функциональном программированию (как, например, я), то этот пост для вас.

Что это такое

Но речь сегодня не о SQL, а о функциональных языках. Именно для них лямбда-исчисление является основой. Функциональные языки далеко не столь популярны, как, например, объектно-ориентированные, но тем не менее прочно занимают свою нишу. Кроме того, многие идеи из функционального программирования и лямда-исчисления постепенно прокрадываются в другие языки, под видом новых фич.

Если вы изучали формальные языки, то знаете о таком понятии как Машина Тьюринга. Эта вычислительная абстракция определяет класс вычислимых функций. Этот класс столь важен, так как по тезису Черча он эквивалентен понятию алгоритма. Другими словами, любую программу, которую можно запрограммировать на вычислительном устройстве, можно воспроизвести и на машине Тьюринга. А для нас главное то, что лямбда-исчисление по мощности эквивалентно машине Тьюринга и определяет этот же класс функций. Причем создателем лямбда-исчисления является тот самый Алонзо Черч!

Основные понятия

В нотации лямбда-исчисления есть всего три типа выражений:

Сразу пара примеров:

Соглашения

Несколько соглашений для понимания, в каком порядке правильно читать выражения:

Области видимости переменных

Определим контекст переменной, в котором она может быть использована. Абстракция ` lambda x.E ` связывает переменную ` x `. В результате мы получаем следующие понятия:

Вычисление лямбда-выражений

Вычисление выражений заключается в последовательном применении подстановок. Подстановкой ` E’ ` вместо ` x ` в ` E \ ` (запись: ` [E’//x]E ` ) называется выполнение двух шагов:

Функции нескольких переменных

Как результат мы получили функцию от одного аргумента, которая возвращает еще одну функцию от одного аргумента. Такое преобразование называется каррирование (в честь Хаскелла Карри назвали и язык программирования, и эту операцию), а функция, возвращающая другую, называется функцией высшего порядка.

Порядок вычислений

Бывают ситуации, когда произвести вычисление можно несколькими способами. Например, в выражении ` (lambda y. (lambda x. x) y) E ` сначала можно подставлять ` y ` вместо ` x ` во внутреннее выражение, либо ` E ` вместо ` y ` во внешнее. Теорема Черча-Рассера говорит о том, что в не зависимости от последовательности операций, если вычисление завершится, результат будет одинаков. Тем не менее, эти два подхода принципиально отличаются. Рассмотрим их подробнее:

Кодирование типов

В чистом лямбда-исчислении есть только функции. Однако, программирование трудно представить без различных типов данных. Идея заключается в том, чтобы закодировать поведение конкретных типов в виде функций.

Аналогично, с помощью лямбда-исчисления можно выразить любые конструкции языков программирования, такие как циклы, ветвления, списки и тд.

Заключение

Источник

Лямбда-исчисление

Лямбда-исчисление (англ. lambda calculus) — формальная система, придуманная в 1930-х годах Алонзо Чёрчем. Лямбда-функция является, по сути, анонимной функцией. Эта концепция показала себя удобной и сейчас активно используется во многих языках программирования.

Содержание

Лямбда-исчисление [ править ]

Пробел во втором правиле является терминалом грамматики. Иногда его обозначают как @, чтобы он не сливался с другими символами в выражении.

В первом случае функция является просто переменной. Во втором происходит аппликация (применение) одной функции к другой. Это аналогично вычислению функции-левого операнда на аргументе-правом операнде. В третьем — абстракция по переменной. В данном случае происходит создание функции одного аргумента с заданными именем аргумента и телом функции.

[math] x\\ (x\ z)\\ (\lambda x.(x\ z))\\ (\lambda z.(\lambda w.((\lambda y.((\lambda x.(x\ z))\ y))\ w)))\\ [/math]

Приоритет операций [ править ]

Свободные и связанные переменные [ править ]

Связанными переменными называются все переменные, по которым выше в дереве разбора были абстракции. Все остальные переменные называются свободными.

Связанные переменные — это аргументы функции. То есть для функции они являются локальными.

α-эквивалетность [ править ]

и замкнуто относительно следующих правил:

[math] P=_\alpha P’ \Rightarrow \forall x \in V: \lambda x.P=_\alpha \lambda x.P’\\ P=_\alpha P’ \Rightarrow \forall Z \in \Lambda : P Z =_\alpha P’Z\\ P=_\alpha P’ \Rightarrow \forall Z \in \Lambda : Z P =_\alpha Z P’\\ P=_\alpha P’ \Rightarrow P’=_\alpha P\\ P=_\alpha P’ \ \& \ P’=_\alpha P» \Rightarrow P=_\alpha P»\\[/math]

β-редукция [ править ]

и замкнуто относительно следующих правил

[math]P\to _\beta P’ \Rightarrow \forall x\in V:\lambda x.P\to _\beta \lambda x.P’\\ P\to _\beta P’ \Rightarrow \forall Z\in \Lambda : P\ Z\to _\beta P’\ Z\\ P\to _\beta P’ \Rightarrow \forall Z\in \Lambda : Z\ P\to _\beta Z\ P'[/math]

Каррирование [ править ]

Нотация Де Брауна [ править ]

Грамматику нотации можно задать как:

Примеры выражений в этой нотации:

Переменная называется свободной, если ей соответствует число, которое больше количества абстракций на пути до неё в дереве разбора.

Определение [ править ]

Введём на основе лямбда-исчисления аналог натуральных чисел, основанный на идее, что натуральное число — это или ноль, или увеличенное на единицу натуральное число.

+1 [ править ]

Сложение [ править ]

Сложение двух чисел похоже на прибавление единицы. Но только надо прибавить не единицу, а второе число.

[math]n[/math] раз применить [math]s[/math] к применённому [math]m[/math] раз [math]s[/math] к [math]z[/math]

[math](\operatorname\ \bar 3\ \bar 3)\ (+1)\ 0 \equiv 6[/math]

[math](\operatorname\ ((\operatorname\ 2\ 5)(+1)\ 0)\ 4)(+1)0 \equiv 11[/math]

Умножение [ править ]

[math](\operatorname \bar 3\ \bar 3)\ (+1)\ 0 \equiv 9[/math]

Возведение в степень [ править ]

It’s a kind of magic

[math](\operatorname\ \bar 3\ (\operatorname\ \bar 3))\ (+1)\ 0 \equiv 81[/math]

Логические значения [ править ]

Стандартные функции булевой логики:

Ещё одной важной функцией является функция проверки, является ли число нулём:

Пара [ править ]

Вычитание [ править ]

В отличие от всех предыдущих функций, вычитание для натуральных чисел определено только в случае, если уменьшаемое больше вычитаемого. Положим в противном случае результат равным нулю. Пусть уже есть функция, которая вычитает из числа единицу. Тогда на её основе легко сделать, собственно, вычитание.

Если вы ничего не поняли, не огорчайтесь. Вычитание придумал Клини, когда ему вырывали зуб мудрости. А сейчас наркоз уже не тот.

Сравнение [ править ]

Комбинатор неподвижной точки [ править ]

Попробуем выразить в лямбда-исчислении какую-нибудь функцию, использующую рекурсию. Например, факториал.

Лямбда исчисление обладаем замечательным свойством: у каждой функции есть неподвижная точка!

Рассмотрим следующую функцию.

[math]\operatorname = \operatorname\ \operatorname[/math]

[math]Y\ = \ \lambda f.(\lambda x.f(x\ x))\ (\lambda x.f(x\ x))[/math]

Деление [ править ]

Воспользовавшись идеей о том, что можно делать рекурсивные функции, сделаем функцию, которая будет искать частное двух чисел.

[math]\operatorname