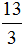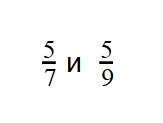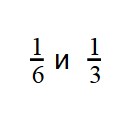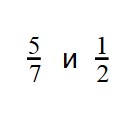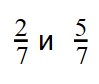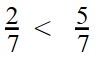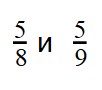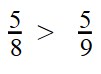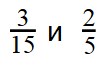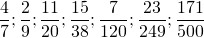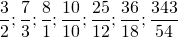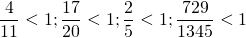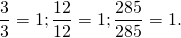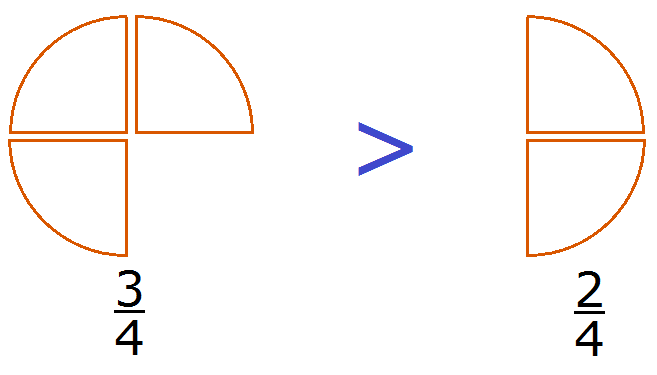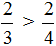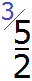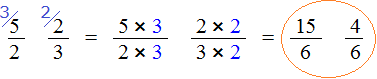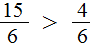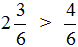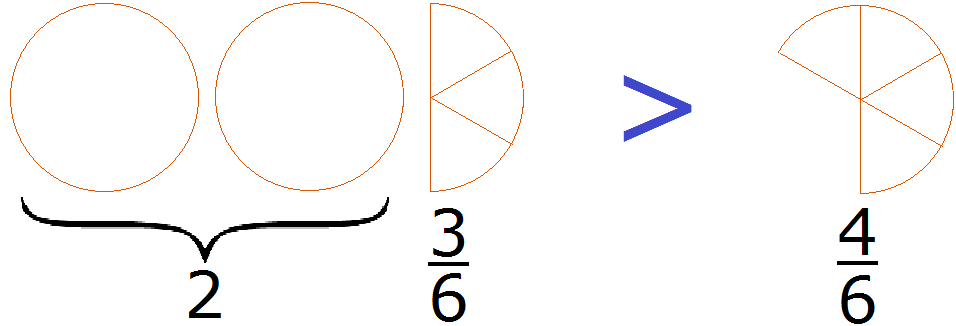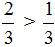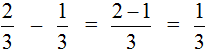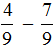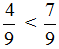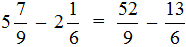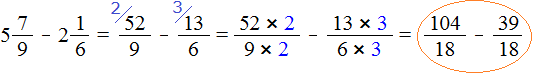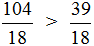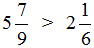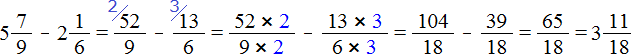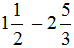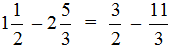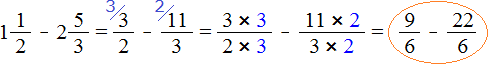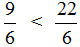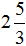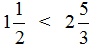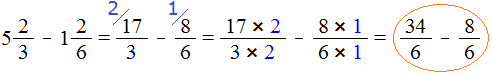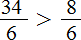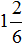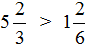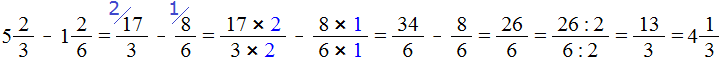Если числитель больше знаменателя что делать с дробью

Сравнение дробей: как правильно

Сравнение дробей с одинаковыми знаменателями

Как и при любом другом сравнении, суть сравнения дробей — в том, чтобы определить меньшую и большую дроби.

Нет ситуации более благоприятной для сравнения, чем дроби с одинаковыми знаменателями. Если вся разница между дробями только в числителях, пользуемся следующим правилом:

Из двух дробей с одинаковыми знаменателями больше дробь с большим числителем. А меньше будет та дробь, числитель которой меньше.

А теперь на примерах.

Пример 1. Сравните дроби:

Пример 3. Сравните дроби:

Как видите, нет ничего сложного в сравнении дробей, если знаменатели равны. Вся задача заключается в том, чтобы определить больший и меньший числитель.

Давайте разберем наглядный пример сравнения дробей. Еще больше наглядных примеров — на курсах по математике в онлайн-школе Skysmart!

Допустим, в торте 6 кусков. Если от целого торта отрезать один кусок — в торте останется 5 кусков.

Понять, что целый торт больше, чем торт без одного куска, можно и без сравнения дробей. Но это же самое правило можно применить и при менее очевидных сравнениях, которые часто встречаются в повседневной жизни.

Сравнение дробей с одинаковыми числителями

Вы уже разобрались со сравнением дробей с одинаковыми знаменателями. Теперь задача чуть усложняется — научимся сравнивать дроби с разными знаменателями, но с одинаковыми числителями.

Если у двух дробей одинаковые числители, то больше будет та дробь, чей знаменатель меньше. А меньше будет дробь с большим знаменателем.

А теперь наши любимые примеры. Погнали!

Пример 1. Сравните дроби:

Пример 3. Сравните дроби:

Сравнение дробей с разными числителями и разными знаменателями

Нет ничего хитрого в сравнении дробей с одинаковыми числителями или знаменателями. Чуть больше усилий потребуется при сравнении дробей, в которых нет ничего одинакового.

Сначала вспомним, как привести дроби к общему знаменателю.
Рассмотрим пример дробей с разными знаменателями.

Давайте потренируемся в сравнении дробей.

Пример 1. Сравните дроби:

При сравнении неправильных дробей с правильными помните, что неправильная дробь всегда больше правильной.

Пример 2: Сравните дроби:

Вычитание смешанных чисел

Вычитание проходит гладко, когда уменьшаемое больше вычитаемого.

В случае, если вычитаемое больше уменьшаемого, разность оказывается отрицательной. В этом нет ничего страшного. Но математика в 5 классе — «положительная», поэтому научимся находить разность смешанных чисел, не скатываясь «в минусы».

При вычитании дробей действует тот же самый принцип: вычитаемое должно быть меньше уменьшаемого. Вот здесь то вам и пригодится навык сравнивать дроби.

Пример 1. Вычислите:

Вычитаемая дробь меньше уменьшаемой

Пример 2.Найдите разность:

Примеры для самопроверки

Теория — это, конечно, хорошо. Но без практики — никуда. Пора потренироваться в решении примеров и закрепить тему сравнения дробей.

Пример 1. Сравните дроби:

Ответ: по правилу сравнения дробей с одинаковыми знаменателями, больше та дробь, у которой числитель больше. Это значит, что

Пример 2. Сравните дроби:

Ответ: по правилу сравнения дробей с разными знаменателями и одинаковыми числителями, больше та дробь, чей знаменатель меньше. Это значит, что

Пример 3. Сравните дроби:

Ответ:.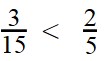

Источник

Неправильная дробь

Что такое неправильная дробь и чем она отличается от правильной?

Дробь, у которой числитель меньше знаменателя, называется правильной.

Дробь, у которой числитель больше или равен знаменателю, называется неправильной.

— правильные, так как у них числитель меньше знаменателя.

— неправильные дроби, так как у них числитель больше знаменателя либо равен ему.

Неправильную дробь можно перевести в правильную, выделив целую часть. Для этого надо разделить числитель на знаменатель с остатком.

Сравнение правильных и неправильных дробей

1) Любая правильная дробь меньше единицы:

2) Любая неправильная дробь больше либо равна единице. Дробь равна единице, если у нее числитель равен знаменателю:

1;\frac<5> <3>> 1;\frac<<49>><<19>> > 1;\frac<<674>><<511>> > 1;\]» title=»Rendered by QuickLaTeX.com»/>

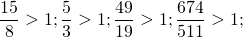
3) Любая неправильная дробь больше любой правильной:

\frac<2><7>;\frac<7><<12>> \frac<<112>><<579>>.\]» title=»Rendered by QuickLaTeX.com»/>

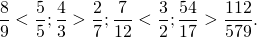
Соответственно, на координатном луче любая неправильная дробь находится правее любой правильной.

Источник

Неправильная дробь

Что такое неправильная дробь

Неправильной называется дробь, числитель которой по своей величине превышает знаменатель либо одинаков с ним.

Основные математические действия с неправильными дробями

Неправильная дробь — полноценный представитель числового множества, поэтому с ней можно производить основные математические действия:

Сравнение

6 / 5 7 / 5 ; 9 / 7 > 8 / 7 ; 5 / 5 = 5 / 5

Однако, бывает необходимо вычислить, насколько значение неправильной дроби больше (либо меньше) значения другой неправильной дроби с иным знаменателем.

Сложение

Определить сумму двух неправильных дробей с одинаковым знаменателем легко: 5/4+7/4=12/4=3

Схематически это можно записать с помощью формулы:

Сложение неправильных дробей с различными знаменателями. Для таких случаев существует два варианта: перевести дроби в смешанные либо использовать правило для перехода к общему знаменателю.

Переход к смешанным дробям осуществляется путем деления числителя на знаменатель (бывает, что с остатком):

Тактика приведения к общему знаменателю при сложении неправильных дробей (и их вычитании) следующая:

Аналогичным образом поступают, когда необходимо провести вычитание с неправильными дробями.

Умножение

При умножении друг на друга двух неправильных дробей получается дробь, числитель которой равен произведению числителей первоначальных дробей, а знаменатель — произведению знаменателей.

Деление

При делении неправильных дробей деление имеет обратное свойство. Делитель необходимо записать наоборот: числитель и знаменатель поменять местами. Когда это проведено, делимое умножают на делитель и получают искомый результат.

Перевод неправильной дроби в смешанную дробь и обратно

Неправильную дробь можно легко перевести в смешанную, произведя следующие действия:

Например, необходимо превратить в смешанную дробь 13/8.

Разделив 13 на 8, получаем 1 и 5/8. Разделив 5 на 8, получаем 0,625. В итоге 1,625.

Бывают случаи, когда нужно произвести обратное действие: превратить смешанную дробь в неправильную. Объяснение изложено в следующей формуле:

Подставим в эту формулу значения. 21 / 3 = ( 1 + 2 * 3 ) / 3 = 7 / 3

Примеры задач

Рассмотрим приведенные выше правила на примерах.

Сложение с одинаковым знаменателем: 8 / 5 + 7 / 5 = 15 / 5 = 3

Объяснение: приводим слагаемые к общему знаменателю. Для этого на знаменатель правой дроби умножаем числитель левой, а знаменатель левой — на числитель правой. В знаменателе дроби-произведения стоит произведение обоих знаменателей. После проведения расчетов получается смешанная дробь 3,625.

Объяснение: приводим вычитаемые к общему знаменателю. Для этого на знаменатель правой дроби умножаем числитель левой, а знаменатель левой — на числитель правой. В знаменателе дроби-частного стоит произведение обоих знаменателей. После проведения расчетов получается смешанная дробь 3,875.

Задача на умножение:

7 / 5 * 9 / 4 = 63 / 20

8 / 6 * 10 / 9 = 80 / 54

Объяснение: умножаем числитель на знаменатель и получаем искомое произведение.

4 / 7 : 2 / 5 = 4 / 7 * 5 / 2 = ( 4 * 5 ) / ( 7 * 2 ) = 20 / 14 = 16 / 14

Поменяв местами числитель и знаменатель в делителе, производим действие умножения двух дробей. После этого в числителе итоговой дроби ставится произведение двух числителей, а в ее знаменателе — произведение двух знаменателей.

Источник

Деление дробей: теория и практика

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие дроби

Дробь — одна из форм представления числа в математике. Это запись, в которой a и b являются числами или выражениями. Существует два формата записи:

Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление. В 5 классе ребята это уже знают.

Дроби бывают двух видов:

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.

Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как пять целых одна четвертая, а записывается — 5 1\4.

Основные свойства дроби

1. Дробь не имеет значения, при условии, если делитель равен нулю.

2. Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.

3. Две дроби a/b и c/d называются равными, если a * d = b * c.

4. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Деление дробных чисел

Деление — арифметическое действие, по которому можно узнать, сколько раз одно число содержится в другом. А еще деление — это обратное действие умножения.

Свойства деления:

1. При делении на единицу получится такое же число:

2. На ноль делить нельзя.

3. Когда делим ноль на любое число, всегда получаем ноль:

4. Когда делим любое число на само себя получаем единичку:

5. Когда делим сумму на какое-либо число, можно разделить на него каждое слагаемое, а потом сложить полученное:

6. Когда делим разность на какое-нибудь число, можно разделить на него уменьшаемое и вычитаемое отдельно и из первого частного вычесть второе:

7. Когда делим произведение двух множителей на число, можно разделить на него любой из множителей и частное умножить на второй множитель:

Записывайся на онлайн обучение по математике, с лучшими учителями! Для учеников с 1 по 11 классы!

Деление обыкновенных дробей

Как делить дробь на дробь? Выполняем следующую последовательность действий:

Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.

Как делить дроби с разными знаменателями? Тут все просто: пользуемся правилами выше, поскольку на практике нам неважно, одинаковые знаменатели или нет.

Деление дроби на натуральное число

Для деления дроби на натуральное число нужно:

Деление натурального числа на дробь

Чтобы поделить натуральное число на обыкновенную дробь нужно:

Деление на смешанное число

Для деления смешанных чисел необходимо:

Если урок в самом разгаре и посчитать нужно быстро — можно воспользоваться онлайн-калькулятором. Вот несколько подходящих:

Источник

Сравнение дробей

Продолжаем изучать дроби. Сегодня мы поговорим об их сравнении. Тема интересная и полезная. Она позволит новичку почувствовать себя учёным в белом халате.

Суть сравнения дробей заключается в том, чтобы узнать какая из двух дробей больше или меньше.

Чтобы ответить на вопрос какая из двух дробей больше или меньше, пользуются операциями отношения, такими как больше (>) или меньше ( )

Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на четыре части. пиццы больше, чем пиццы:

Каждый согласится с тем, что первая пицца больше, чем вторая.

Сравнение дробей с одинаковыми числителями

Следующий случай это когда числители дробей одинаковые, но знаменатели разные. Для таких случаев предусмотрено следующее правило:

Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше. И соответственно меньше та дробь, у которой знаменатель больше.

Например, сравним дроби и . У этих дробей одинаковые числители. У дроби знаменатель меньше, чем у дроби . Значит дробь больше, чем дробь . Так и отвечаем:

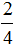
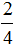
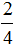
Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на три и четыре части. пиццы больше, чем пиццы:

Каждый согласится с тем, что первая пицца больше, чем вторая.

Сравнение дробей с разными числителями и разными знаменателями

Чтобы ответить на вопрос, какая из этих дробей больше или меньше, нужно привести их к одинаковому (общему) знаменателю. Затем можно будет легко определить какая дробь больше или меньше.

Приведём дроби и к одинаковому (общему) знаменателю. Найдём наименьшее общее кратное (НОК) знаменателей обеих дробей. НОК знаменателей дробей и это число 6.

Теперь находим дополнительные множители для каждой дроби. Разделим НОК на знаменатель первой дроби . НОК это число 6, а знаменатель первой дроби это число 2. Делим 6 на 2, получаем дополнительный множитель 3. Записываем его над первой дробью:

Умножим дроби на свои дополнительные множители:

Мы пришли к тому что дроби, у которых были разные знаменатели, превратились в дроби, у которых одинаковые знаменатели. А как сравнивать такие дроби мы уже знаем. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше:

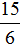
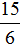
Правило правилом, а мы попробуем разобраться почему больше, чем . Для этого выделим целую часть в неправильной дроби . В дроби ничего выделять не нужно, поскольку эта дробь уже правильная.

После выделения целой части в дроби 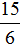, получим следующее выражение:

Теперь можно легко понять, почему 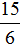больше, чем . Давайте нарисуем эти дроби в виде пицц:

2 целые пиццы и пиццы, больше чем пиццы.

Вычитание смешанных чисел. Сложные случаи.

Вычитая смешанные числа иногда можно обнаружить, что всё идёт не так гладко как хотелось бы.

При вычитании чисел уменьшаемое должно быть больше вычитаемого. Только в этом случае будет получен нормальный ответ.

Уменьшаемое 10 больше вычитаемого 8, поэтому мы получили нормальный ответ 2.

А теперь посмотрим, что будет если уменьшаемое окажется меньше вычитаемого. Пример 5 − 7 = −2

В этом случае мы выходим за пределы привычных для нас чисел и попадаем в мир отрицательных чисел, где нам ходить пока рано, а то и опасно. Чтобы работать с отрицательными числами, нужна соответствующая математическая подготовка, которую мы ещё не получили.

Если при решении примеров на вычитание вы обнаружите, что уменьшаемое меньше вычитаемого, то можете пока пропустить такой пример. Работать с отрицательными числами допустимо только после их изучения.

С дробями ситуация та же самая. Уменьшаемое должно быть больше вычитаемого. Только в этом случае можно будет получить нормальный ответ. А чтобы понять больше ли уменьшаемая дробь, чем вычитаемая, нужно уметь сравнить эти дроби.

Например, решим пример .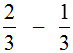

Это пример на вычитание. Чтобы решить его, нужно проверить больше ли уменьшаемая дробь, чем вычитаемая. больше чем

поэтому смело можем вернуться к примеру и решить его:

Теперь решим такой пример

Проверяем больше ли уменьшаемая дробь, чем вычитаемая. Обнаруживаем, что она меньше:

В этом случае разумнее остановиться и не продолжать дальнейшее вычисление. Вернёмся к этому примеру, когда изучим отрицательные числа.

Смешанные числа перед вычитанием тоже желательно проверять. Например, найдём значение выражения .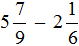

Сначала проверим больше ли уменьшаемое смешанное число, чем вычитаемое. Для этого переведём смешанные числа в неправильные дроби:

Получили дроби с разными числителями и разными знаменателями. Чтобы сравнить такие дроби, нужно привести их к одинаковому (общему) знаменателю. Не будем подробно расписывать как это сделать. Если испытываете затруднения на этом моменте, обязательно изучите действия с дробями.

После приведения дробей к одинаковому знаменателю, получаем следующее выражение:

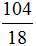
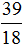
Теперь нужно сравнить дроби и . Это дроби с одинаковыми знаменателями. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.

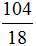
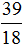
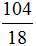
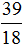
У дроби числитель больше, чем у дроби . Значит дробь больше, чем дробь .

А это значит что уменьшаемое 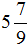больше, чем вычитаемое

А значит мы можем вернуться к нашему примеру и смело решить его:

Пример 3. Найти значение выражения

Проверим больше ли уменьшаемое, чем вычитаемое.

Переведём смешанные числа в неправильные дроби:

Получили дроби с разными числителями и разными знаменателями. Приведем данные дроби к одинаковому (общему) знаменателю:

Теперь сравним дроби и . У дроби числитель меньше, чем у дроби , значит дробь меньше, чем дробь

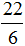
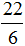
А это значит, что и уменьшаемое 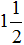меньше, чем вычитаемое

А это гарантировано приведёт нас в мир отрицательных чисел. Поэтому разумнее остановиться на этом месте и не продолжать вычисление. Продолжим его после изучения отрицательных чисел.

Пример 4. Найти значение выражения

Проверим больше ли уменьшаемое, чем вычитаемое.

Переведём смешанные числа в неправильные дроби:

Получили дроби с разными числителями и разными знаменателями. Приведем их к одинаковому (общему) знаменателю:

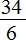
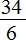
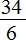
Теперь нужно сравнить дроби и . У дроби числитель больше, чем у дроби . Значит дробь больше, чем дробь .

А это значит, что уменьшаемое 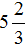больше, чем вычитаемое

Поэтому мы смело можем продолжить вычисление нашего примера:

Сначала мы получили ответ . Эту дробь мы сократили на 2 и получили дробь , но такой ответ нас тоже не устроил и мы выделили целую часть в этом ответе. В итоге получили ответ .

Источник