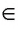Если две прямые имеют общую точку о то говорят что они

Точки, Прямые и Отрезки — Определения и Свойства

Вспомним определения точки и прямой:

Точка — это фигура в геометрии, не имеющая никаких
измеримых характеристик, кроме координат.

Прямая — это фигура в геометрии, которая не
имеет ни начала, ни конца.

Для изображения прямых на чертеже используют линейку, но
при этом можно изобразить только часть прямой, а вся прямая бесконечна.
Принято обозначать прямые малыми латинскими буквами, а точки —
большими латинскими буквами.

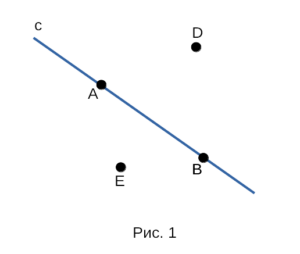
На рисунке 1 изображены прямая c и точки A, B, D, E. Точки А и B
лежат на прямой c, а точки D и E не лежат. Прямая с проходит через
точки A и B, но не проходит через точки С и D. Также заметим, что через
точки A и В нельзя провести другую прямую, не совпадающую с прямой c.

Через любые две точки можно провести прямую,
и притом только одну.

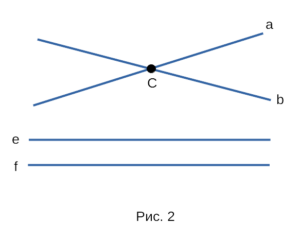
Если две прямые имеют общую точку, то можно сказать,
что они пересекаются. На рисунке 2 прямые a и b
пересекаются в общей точке C, а прямые e и f не
пересекаются, так как не имеют общей точки. Две прямые
не могут иметь двух и более общих точек, так как через две
и более точек проходит только одна прямая.

Две прямые имеют только одну общую точку,
либо не имеют общих точек.

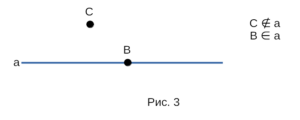
Прямую, на которой отмечены две точки, иногда обозначают двумя
буквами. Для обозначения того, лежит ли точка на прямой или нет,
используют математический символ ∈ или ∉. Пример использования
математического символа ∈ или ∉ на рисунке 3.

Часть прямой ограниченная двумя точками называется отрезком. Точки,
ограничивающие отрезок, называются концами отрезка. Отрезок имеет
начало и конец. Пример отрезка на рисунке 4.

Источник

§ 1. Прямая и отрезок

Точки, прямые, отрезки

В этой главе речь пойдёт о простейших геометрических фигурах-точках, прямых, отрезках, лучах, углах. С ними вы познакомились на уроках математики в 5 и 6 классах. К тому, что вы знаете об этих фигурах, мы добавим новые сведения, и они послужат нам опорой для изучения в следующих главах свойств более сложных фигур. Ещё мы расскажем о практических приложениях геометрии —о том, как геометрия помогает прокладывать прямолинейные дороги и как проводится измерение углов на местности.

Вспомним, что нам известно о точках и прямых. Мы знаем, что для изображения прямых на чертеже пользуются линейкой (рис. 4), но при этом можно изобразить лишь часть прямой, а всю прямую мы представляем себе простирающейся бесконечно в обе стороны.

Обычно прямые обозначают малыми латинскими буквами, а точки — большими латинскими буквами. На рисунке 5 изображены прямая а и точки А, В, С и D. Точки А и В лежат на прямой а, а точки С и D не лежат на этой прямой. Можно сказать, что прямая а проходит через точки А и В, но не проходит через точки С и В. Отметим, что через точки А и В нельзя провести другую прямую, не совпадающую с прямой а.

Рассмотрим теперь две прямые. Если они имеют общую точку, то говорят, что эти прямые пересекаются. На рисунке 6 прямые а и b пересекаются в точке О, а прямые р и q не пересекаются. Две прямые не могут иметь двух и более общих точек. В самом деле, если бы две прямые имели две общие точки, то каждая из прямых проходила бы через эти точки. Но через две точки проходит только одна прямая. Таким образом, можно сделать вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Прямую, на которой отмечены две точки, например А и В, иногда обозначают двумя буквами: АВ или ВА. Для краткости вместо слов «точка А лежит на прямой а» используют запись А ∈ а, а вместо слов «точка В не лежит на прямой а» — запись В ∉ а.

На рисунке 7, а выделена часть прямой, ограниченная двумя точками. Такая часть прямой называется отрезком. Точки, ограничивающие отрезок, называются его концами. На рисунке 7, б изображён отрезок с концами А и В. Такой отрезок обозначается АВ или В А. Отрезок АВ содержит точки А и В и все точки прямой АВ, лежащие между А и В.

Провешивание прямой на местности

Решим такую задачу: с помощью данной линейки построить отрезок более длинный, чем сама линейка. С этой целью приложим к листу бумаги линейку, отметим точки А и В и какую-нибудь точку С, лежащую между А к В (рис. 8, а). Затем передвинем линейку вправо так, чтобы её левый конец оказался около точки С, и отметим точку D около правого конца линейки (рис. 8, б). Точки А, В, С и D лежат на одной прямой. Если мы проведём теперь отрезок АВ, а затем отрезок BD, то получим отрезок AD, более длинный, чем линейка.

Аналогичный приём используется для «проведения» длинных отрезков прямых на местности. Этот приём заключается в следующем. Сначала отмечают какие-нибудь точки А и В. Для этой цели используют две вехи — шесты длиной около 2 м, заострённые на одном конце для того, чтобы их можно было воткнуть в землю. Третью веху ставят так, чтобы вехи, стоящие в точках А и В, закрывали её от наблюдателя, находящегося в точке А (точка С на рисунке 9). Следующую веху ставят так, чтобы её закрывали вехи, стоящие в точках В и С, и т. д.

Описанный приём называется провешиванием прямой (от слова «веха»). Он широко используется на практике, например при рубке лесных просек, при прокладывании шоссейных или железных дорог, линий высоковольтных передач и т. д.

Практические задания

1. Проведите прямую, обозначьте её буквой а и отметьте точки А и В, лежащие на этой прямой, и точки Р, Q и R, не лежащие на ней. Опишите взаимное расположение точек А, В, Р, Q, R и прямой а, используя символы ∉ и ∈.

2. Отметьте три точки А, В и С, не лежащие на одной прямой, и проведите прямые АВ, ВС и СА.

3. Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.

4. Отметьте точки А, В, С, D так, чтобы точки А, В, С лежали на одной прямой, а точка D не лежала на ней. Через каждые две точки проведите прямую. Сколько получилось прямых?

5. Проведите прямую а и отметьте на ней точки А и В. Отметьте: а) точки М и N, лежащие на отрезке АВ; б) точки Р и Q, лежащие на прямой а, но не лежащие на отрезке АВ; в) точки R и S, не лежащие на прямой а.

6. Проведите прямую и отметьте на ней три точки. Сколько отрезков получилось на прямой?

7. На рисунке 10 изображена прямая, на ней отмечены точки А, В, С и D. Назовите все отрезки: а) на которых лежит точка С; б) на которых не лежит точка В.

Источник

Прямая и ее части – что такое в математике, правило

В геометрии любой объект состоит из базовых элементов: точек, прямых и плоскостей. Любая фигура, не важно, плоская она или объемная, будет состоять из этих элементов. Определение точки понятно, но вот как понять, что такое прямая и как она может быть бесконечной – в 5 классе не так просто разобраться.

Определение прямой

Определение прямой начинается с определения линии. Что такое линия? Это множество точек, соединенных между собой. Линия может быть прямой, кривой, ломанной, непрерывной и даже разомкнутой. И именно из-за этого разнообразия линии очень трудно определить в пространстве. Непонятно, как пройдет та или иная кривая, когда выйдет за пределы листа. Поэтому был выделен отдельный вид линий – прямые.

Когда в разговоре вы слышите прямая – люди имеют в виду прямую линию, но последнее слово в словосочетании принято опускать.

Что такое прямая в математике? Прямые это бесконечные непрерывные линии, которые не имеют искривлений. Первое правило линий: через любые две точки можно провести линию. А вот через три точки уже не всегда. Чаще всего через три точки можно провести три прямых.

Если прямая проходит через три точки, то про эти точки говорят, что они лежат на одной прямой. Прямые, как правило, обозначают малой латинской буквой или по названию двух точек на прямой.

Почему двух, а не трех? Очень просто: через две точки может пройти только одна прямая. Тогда как через одну: бесконечное множество. А три точки не имеет смысла использовать: ни к чему усложнять обозначение.

Взаимное расположение прямых

Две прямые в пространстве могут располагаться по-разному. Самый простой и частый случай это пересечение. Если две прямые имеют одну общую точку, про такие прямые говорят, что они пересекаются.

Рис. 2. Взаимное расположение прямых.

А как прямые назвать, если они не пересекаются? Тогда – параллельные, то есть прямые, которые не имеют общих точек.

А что будет, если у двух прямых две и больше общих точек? Тогда прямые совпадут.

При пересечении двух прямых образуется две пар вертикальных углов. Вертикальные углы в каждой паре равны между собой.

Если угол пересечения равен 90 градусов, то прямые перпендикулярны друг другу.

Рис. 3. Пересечение прямых.

Точка на прямой

Точка на прямой это почти магия. Сама по себе прямая это множество точек, но стоит отметить одну из них и геометрическую фигуру можно назвать как прямой, так и двумя лучами с началом в одной точке. Если поставить две точки на прямой, то они будут отделять часть прямой, которую называют отрезком.

Любой отрезок является частью прямой.

Что мы узнали?

Мы дали определении линиям, выделили виды линий, а так же рассмотрели, какая из линий может называться прямой. Поговорили о том, как обозначаются прямые и как они могут располагаться в пространстве относительно друг друга. Выяснили, что точка на прямой может сделать из прямой отрезок или луч.

Источник

Геометрия. 10 класс

Введение в стереометрию

Введение в стереометрию

Необходимо запомнить

Стереометрия – это раздел геометрии, в котором изучаются свойства фигур в пространстве.

Простейшими (основными) фигурами в пространстве являются точки, прямые и плоскости.

Аксиома 1: Через 3 точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

Аксиома 2: Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются.

Аксиома 3: Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Теорема 1: Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

Теорема 2: Через две пересекающиеся прямые проходит плоскость, и, причём только одна.

Введение в стереометрию

Аксиоматический метод – способ построения научной теории, при котором в основу теории кладутся некоторые исходные положения, называемые аксиомами теории, а все остальные предложения теории получаются как логические следствия аксиом.

Определение из математической энциклопедии.

Аксиоматический метод появился в Древней Греции, а сейчас применяется во всех теоретических науках, прежде всего в математике. Аксиоматический метод построения научной теории заключается в следующем: выделяются основные понятия, формулируются аксиомы теории, а все остальные утверждения выводятся логическим путём, опираясь на них.

Основные понятия выделяются следующим образом. Известно, что одно понятие должно разъясняться с помощью других, которые, в свою очередь, тоже определяются с помощью каких-то известных понятий. Таким образом, мы приходим к элементарным понятиям, которые нельзя определить через другие.

Определение (дефиниция) – установление смысла незнакомого термина с помощью терминов знакомых и уже осмысленных или путём включения в контекст знакомых слов (контекстуальное определение), или явного формулирования равенства, в левую часть которого входит определяемый термин, а в правую – определяющее выражение, содержащее только знакомые термины.

Теорема (греч. theorema, от theoreo – рассматриваю), в математике – предложение (утверждение), устанавливаемое при помощи доказательства (в противоположность аксиоме). Теорема обычно состоит из условия и заключения. Например, в теореме: если в треугольнике один из углов прямой, то два других – острые, после слова «если» стоит условие, а после «то» – заключение.

Эти понятия и называются основными. Когда мы доказываем утверждение, теорему, то опираемся на предпосылки, которые считаются уже доказанными. Но эти предпосылки тоже доказывались, их нужно было обосновать. В конце концов, мы приходим к недоказываемым утверждениям и принимаем их без доказательства. Эти утверждения называются аксиомами.

Набор аксиом должен быть таким, чтобы, опираясь на него, можно было доказать дальнейшие утверждения. Выделив основные понятия и сформулировав аксиомы, далее мы выводим теоремы и другие понятия логическим путём.

«Начала» начинаются с изложения 23 определений и 10 аксиом. Первые пять аксиом – «общие понятия», остальные называются «постулатами».

Пять «общих понятий» Евклида являются принципами измерения длин, углов, площадей, объёмов: «равные одному и тому же равны между собой», «если к равным прибавить равные, суммы равны между собой», «если от равных отнять равные, остатки равны между собой», «совмещающиеся друг с другом равны между собой», «целое больше части».

Первые два постулата определяют действия с помощью идеальной линейки, третий – с помощью идеального циркуля. Четвёртый, «все прямые углы равны между собой», является излишним, так как его можно вывести из остальных аксиом. Последний, пятый постулат гласил: «Если прямая падает на две прямые и образует внутренние односторонние углы в сумме меньше двух прямых, то, при неограниченном продолжении этих двух прямых, они пересекутся с той стороны, где углы меньше двух прямых».

В начале XIX века H. И. Лобачевским и Я. Больяй (J. Bolyai) была открыта, так называемая, неевклидова геометрия, что явилось толчком к дальнейшему развитию аксиоматического метода. Они установили, что, заменив привычный и, казалось бы, единственно «объективно истинный» 5 постулат Евклида о параллельных его отрицанием, можно развивать чисто логическим путем геометрическую теорию, столь же стройную и богатую содержанием, как и геометрия Евклида. Этот факт заставил математиков XIX века обратить внимание на дедуктивный способ построения математической теорий, что повлекло за собой возникновение новой проблематики, связанной с самим понятием аксиоматического метода, и формальной (аксиоматической) математической теории.

Источник

На уроках математики в предыдущих классах и в главе 1 вы уже познакомились со свойствами некоторых геометрических фигур. Теперь вы приступаете к систематическому изучению геометрии.

Как уже отмечалось ранее, основными геометрическими фигурами являются точка, прямая, плоскость. Представление об этих фигурах вы уже имеете.

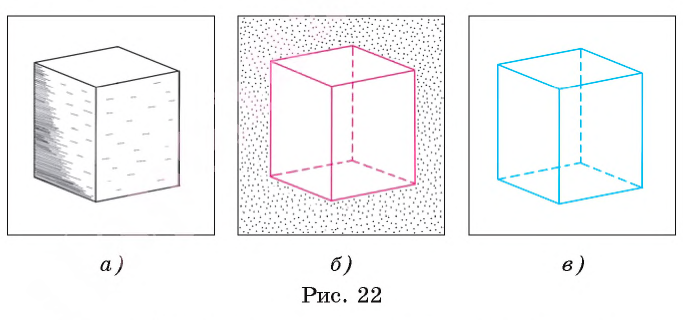
Например, туго натянутая нить дает представление о части прямой, страница книги или грань прямоугольного параллелепипеда — о части плоскости (рис. 22, а, б, в).

Если точка А принадлежит прямой b, то говорят, что прямая b проходит через точку А. Это записывают так: А

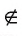
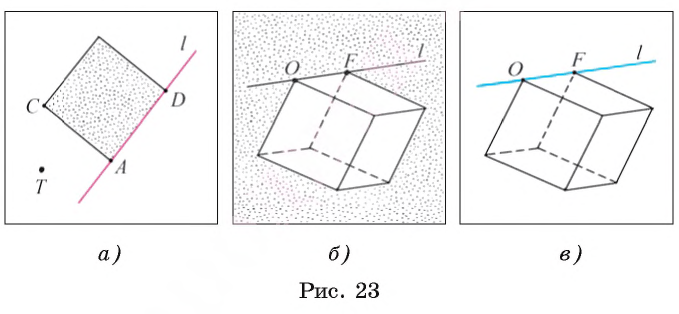
Если точка А не принадлежит прямой b, то говорят, что прямая b не проходит через точку А. В этом случае используется запись А b (читают: «Точка А не принадлежит прямой b», «Точка А не лежит на прямой b» или «Прямая b не проходит через точку А»).

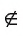
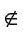
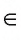
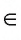
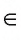
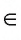
Например, на рисунке 23, а изображены точка С — вершина квадрата и точка Т, не лежащие на прямой l (С l, Т l), проходящей через вершины А и D квадрата (А l, D l). На рисунке 23, б, в изображена прямая l, проходящая через вершины О и F куба (O l, F l).

В курсе геометрии понятия « точка», « прямая» и «плоскость» относятся к основным понятиям и принимаются без определений, другие геометрические понятия определяются через основные. К основным понятиям относятся также понятия «принадлежать» и «лежать между». Свойства геометрических фигур устанавливаются путем логических рассуждений на основе некоторых утверждений (аксиом), которые принимаются без доказательств. Аксиомы выражают основные свойства геометрических фигур, которые соответствуют формам и отношениям, наблюдаемым в окружающем пространстве.

Утверждение, которое обосновывается путем логических рассуждений, называется теоремой, а само обоснование — доказательством. Доказать теорему — это значит путем рассуждений обосновать, что она следует из некоторых аксиом или ранее доказанных теорем.

Взаимное расположение точек и прямых на плоскости характеризуют следующие основные свойства (аксиомы):

Прямая, которая проходит через точки А и В, обозначается АВ или ВА.

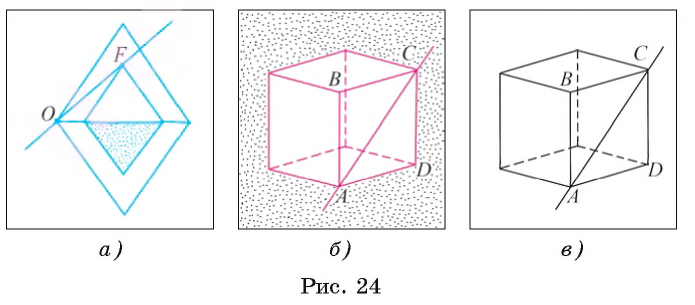
Например, на рисунке 24, а изображена прямая ОF, которая проходит через точки О и F, а на рисунке 24, б, в показана прямая АС, которая проходит через вершины А и С куба и лежит в той же плоскости, что и грань АВСD куба.

1 Здесь и в дальнейшем, говоря «две точки», «две прямые» и т. д., будем считать, что эти точки, прямые и т. д. различны.

Пересекающиеся и параллельные прямые

Рассмотрим понятия пересекающихся и параллельных прямых.

Определение. Две прямые называются пересекающимися, если они имеют одну общую точку.

Если прямые а и b пересекаются в точке О, то это обозначается так: О = а b (читают: «Прямые а и b пересекаются в точке О»).

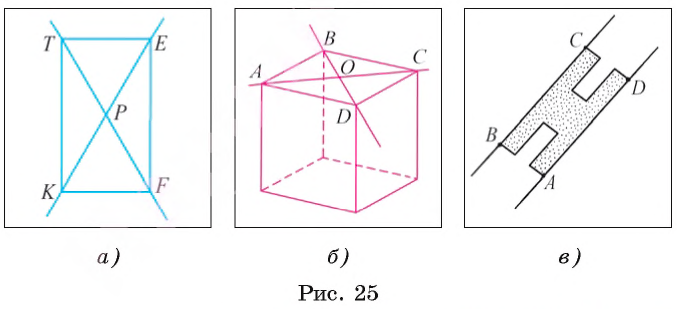
Например, на рисунке 25, а изображены прямые КЕ и TF, которые проходят через вершины прямоугольника и пересекаются в точке Р (Р =TF КЕ).

На рисунке 25, B изображены прямые АС и BD, которые проходят через вершины куба и пересекаются в точке О (О = АС 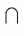ВD).

Определение. Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются.

Параллельные прямые l₁ и l₂ обозначаются так: l₁ 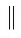l₂ (читают: «Прямая l₁ параллельна прямой l₂ »).

Например, на рисунке 25, в изображены параллельные прямые ВС и АD (ВС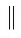АD).

Теорема. Если две прямые плоскости имеют общую точку, то она единственная.

Пусть две прямые а и b имеют общую точку О. Докажем, что других общих точек эти прямые не имеют. Допустим, что прямые а и b имеют еще одну общую точку O₁. Тогда получается, что через точки O и O₁ проходят две прямые а и b. Но этого быть не может, так как по аксиоме А3 через две точки проходит единственная прямая. Таким образом, наше предположение неверно, и прямые а и b имеют единственную общую точку.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник