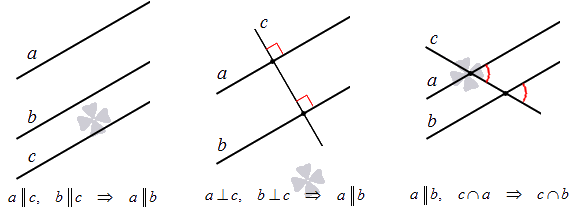Если прямые имеют общую точку то говорят что эти прямые совпадают

Точки, Прямые и Отрезки — Определения и Свойства

Вспомним определения точки и прямой:

Точка — это фигура в геометрии, не имеющая никаких
измеримых характеристик, кроме координат.

Прямая — это фигура в геометрии, которая не
имеет ни начала, ни конца.

Для изображения прямых на чертеже используют линейку, но
при этом можно изобразить только часть прямой, а вся прямая бесконечна.
Принято обозначать прямые малыми латинскими буквами, а точки —
большими латинскими буквами.

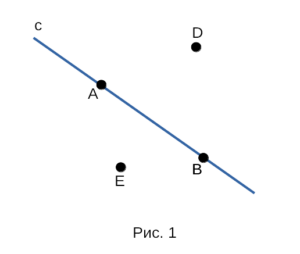
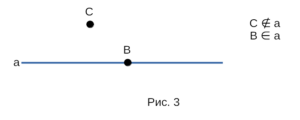
На рисунке 1 изображены прямая c и точки A, B, D, E. Точки А и B
лежат на прямой c, а точки D и E не лежат. Прямая с проходит через
точки A и B, но не проходит через точки С и D. Также заметим, что через
точки A и В нельзя провести другую прямую, не совпадающую с прямой c.

Через любые две точки можно провести прямую,
и притом только одну.

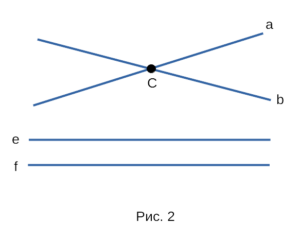
Если две прямые имеют общую точку, то можно сказать,
что они пересекаются. На рисунке 2 прямые a и b
пересекаются в общей точке C, а прямые e и f не
пересекаются, так как не имеют общей точки. Две прямые
не могут иметь двух и более общих точек, так как через две
и более точек проходит только одна прямая.

Две прямые имеют только одну общую точку,
либо не имеют общих точек.

Прямую, на которой отмечены две точки, иногда обозначают двумя
буквами. Для обозначения того, лежит ли точка на прямой или нет,
используют математический символ ∈ или ∉. Пример использования
математического символа ∈ или ∉ на рисунке 3.

Часть прямой ограниченная двумя точками называется отрезком. Точки,
ограничивающие отрезок, называются концами отрезка. Отрезок имеет
начало и конец. Пример отрезка на рисунке 4.

Источник

Лекция по теме: «Основные понятия стереометрии»

Первейшим гарантом непогрешимости математического мышления считается то, что исходным пунктом рассуждений и действий в этой науке служат аксиомы.

выдающийся физиолог, психолог

ОСНОВНЫЕ ПОНЯТИЯ СТЕРЕОМЕТРИИ

1 Структура курса геометрии

2 Определения и обозначения

3 Основные свойства плоскости

4 Взаимное расположение прямых и плоскостей в пространстве

1 Структура курса геометрии

Стереометрия — это раздел геометрии, в котором изучаются фигуры в пространстве. Она является второй составляющей геометрии и строится так же, как и планиметрия.

В стереометрии свойства геометрических фигур устанавливаются с помощью доказательства теорем (из греч. — рассматриваю), которые основываются на аксиомах (из греч. — считаю достойным, настаиваю, требую) — математических предложениях, принимаемых без доказательства

2 Определения и обозначения

Плоскость понимают также как множество точек.

3 Основные свойства плоскости

Основные свойства точек, прямых и плоскостей, касающиеся их взаимного расположения, выражены в аксиомах.

Система аксиом стереометрии состоит из двух групп. Первая из них включает все аксиомы планиметрии. Они выполняются в каждой плоскости пространства. Эти аксиомы вам известны из курса планиметрии. Здесь рассмотрим группу аксиом, выражающую основные свойства плоскостей в пространстве.

1 Через любые три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну

2 Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.

3 Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.

Утверждение, истинность которого доказана и которое используют для доказательства других утверждений, называют теоремой. Простейшими теоремами являются следствия из аксиом стереометрии.

Теорема 1 Через прямую и точку, не принадлежащую ей, можно провести плоскость и притом только одну

Доказательство. Данная точка и две точки прямой составляют три точки, не лежащие на одной прямой. По аксиоме 1 через них проходит единственная плоскость. По аксиоме 3 данная прямая лежит в этой плоскости.

Теорема 2 Через две пересекающиеся прямые можно провести плоскость и притом только одну.

Доказательство. На каждой из прямых можно взять по одной необщей точке. Вместе с точкой пересечения прямых они образуют три точки, не лежащие на одной прямой. По аксиоме 1 через них проходит единственная плоскость. По аксиоме 3 обе прямые лежат в этой плоскости.

Теорема 3 Через две параллельные прямые можно провести плоскость и притом только одну.

Доказательство. По теореме 1 через одну из параллельных прямых и произвольную точку другой прямой можно провести плоскость, и притом только одну.

Если учесть вышеизложенное, то можно сделать вывод, что плоскость однозначно определяют:

1) три точки, не лежащие на одной прямой;

2) прямая и точка, не принадлежащая этой прямой;

3) две пересекающиеся прямые;

4) две параллельные прямые.

4 Взаимное расположение прямых и плоскостей в пространстве

Взаимное расположение прямых в пространстве можно свести к следующим случаям.

1 Прямые пересекаются, тогда они лежат в одной плоскости.

2 Прямые параллельны — тогда они лежат в одной плоскости

3 Прямые не пересекаются и не параллельны — такие прямые называются скрещивающимися.

4 Прямые совпадают, если они имеют по крайней мере две общие точки

Возможны следующие варианты взаимного расположения прямой и плоскости в пространстве:

1) Прямая и плоскость имеют по крайней мере две общие точки. Тогда прямая лежит в плоскости, то есть прямая и плоскость имеют множество общих точек;

2) Прямая и плоскость имеют одну общую точку. Возможность такого размещения прямых и плоскостей обеспечивается тем, что вне плоскости являются точки пространства. Произвольная точка плоскости и точка вне плоскости определяют прямую, которая имеет с плоскостью одну общую точку, то есть пересекает ее.

3) Прямая и плоскость не имеют общих точек, то есть не пересекаются. Прямая и плоскость, которые не имеют общих точек, называются параллельными

Плоскости в пространстве могут принимать следующие положения друг относительно друга:

1 Две плоскости пересекаются по прямой — в этом случае они не имеют других общих точек вне этой прямой

2 Плоскости совпадают

3 Если две разные плоскости не имеют общих точек, то они называются параллельными.

1 Какой раздел геометрии называется стереометрией?

2 Какие предложения называются аксиомами? Теоремами?

3 Сформулируйте аксиомы плоскости и следствия из них.

4 Назовите возможные варианты взаимного расположения прямых в пространстве.

5 Перечислите возможные варианты взаимного расположения прямой и плоскости в пространстве.

6 Приведите возможные варианты взаимного расположения плоскостей в пространстве.

Задачи, задания, вопросы

№3 Выберите для двух различных плоскостей и одинаковые по смыслу утверждения.

1) Плоскости и пересекаются;

2) плоскости и имеют лишь одну общую точку;

3) плоскости и имеют общую точку;

4) плоскости и имеют не больше двух общих точек;

5) плоскости и имеют общую прямую.

№5 Плоскости пересекаются. Определите количество общих прямых, которые они могут иметь.

№7 Выберите четыре утверждения, которые определяют единственность плоскости.

1) Любые две точки пространства;

2) любая прямая пространства и точка на ней;

3) любая прямая пространства и точка вне нее;

4) любые три прямых пространства;

5) любые три точки пространства;

6) любые две параллельные прямые;

7) любые две прямые;

8) любые две пересекающиеся прямые.

№13 Выберите правильное утверждение.

1) Через точку пространства, которая не лежит на прямой, можно провести множество прямых, которые параллельные данной;

2) две прямые, параллельные третьей, пересекаются в одной точке;

3) если две точки прямой принадлежат плоскости, то прямая пересекает плоскость;

4) через прямую и точку вне прямой можно провести две различные плоскости;

5) через точку пространства, не лежащую на плоскости, можно провести множество прямых, которые будут пересекать эту плоскость.

1) — единственная возможная плоскость, параллельная плоскости ;

2) — единственная возможная плоскость, пересекающая плоскость ;

3) — единственная возможная плоскость, параллельная плоскости ;

4) — единственная возможная плоскость, пересекающая плоскость ;

Математика: учебник для ссузов / Н. В. Богомолов, П. И. Самойленко. — 7-е изд., стереотип. — М.: Дрофа, 2010., стр. 320-323

Геометрия. 10-11 классы: учебник для учащихся общеобразоват. учреждений: базовый и профил. уровни / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. — 18-е изд., — М.: Просвещение, 2009, стр. 3-8.

Математика: підручник для 10 кл. загальноосвітніх навчальних закладів: рівень стандарту / О.М. Афанасьєва, Я.С. Бродський, О.Л. Павлов, А.К. Сліпенко. – Тернопіль: Навчальна книга – Богдан, 2010, стор. 127-133, 135-137

Источник

Геометрия 7 класс.
Точка, прямая и отрезок

Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.

Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.

Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.

Точка — элементарная фигура, не имеющая частей.

Прямая состоит из множества точек и простирается бесконечно в обе стороны.

То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:

Как обозначить прямую

Прямую обычно обозначают одной маленькой латинской буквой.

Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.

Задача № 1 из учебника Атанасян 7-9 класс

Решение задачи

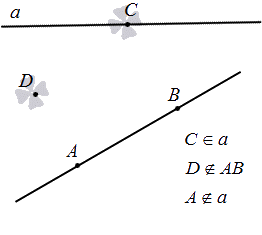
Опишем взаимное расположение точек и прямой.

Как обозначается пересечение прямых

Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).

Прямые e и f не имеют общей точки — т.е. они не пересекаются.

Взаимное расположение прямой и точек

Через одну точку (·)A можно провести сколько угодно прямых.

Через две точки (·)A и (·)B можно провести только одну прямую.

Сколько общих точек имеют две прямые

Две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.

Первый случай расположения прямых

На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.

Второй случай расположения прямых

Третий случай расположения прямых

Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Задача № 3 из учебника Атанасян 7-9 класс

Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.

Решение задачи

Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.

Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.

Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.

Ответ: точек пересечения получается одна или три.

Что такое отрезок

Отрезок — часть прямой, ограниченная двумя точками.

В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.

Источник

Если 2 прямые имеют общую точку, то через них можно провести только?

Если 2 прямые имеют общую точку, то через них можно провести только?

2. одно пространство.

Прямая (а) не имеет общих точек с плоскостью (d)?

Прямая (а) не имеет общих точек с плоскостью (d).

Сколько всего разных прямых, скрещивающихся с прямой (а), можно провести через точку, взятую с плоскости (d)?

1) Ни одной, 2) одну, 3) множество, 4) ни одной либо множество.

1) Любые три различные прямые проходят через одну общую точку?

1) Любые три различные прямые проходят через одну общую точку.

2) Существует точка плоскости, не лежащая на данной прямой, через которую нельзя провести на плоскости ни одной прямой, параллельной данной.

3) Если угол равен 47°.

То смежный с ним угол равен 47°.

4) Через любые две различные точки плоскости можно провести прямую.

5) Существуют две различные прямые, не проходящие через одну общую точку.

Выберите номера верных утверждений.

Если прямая и плоскость имеют только одну общую точку, то прямая а)пересекает плоскость ; б)лежит в плоскости ; в)параллельна плоскости?

Если прямая и плоскость имеют только одну общую точку, то прямая а)пересекает плоскость ; б)лежит в плоскости ; в)параллельна плоскости.

В каком случае 3 точки в пространстве не определяют положение плоскости, проходящей через эти точки?

В каком случае 3 точки в пространстве не определяют положение плоскости, проходящей через эти точки?

Могут ли 2 различные плоскости иметь только одну общую точку?

Точка М не лежит на прямой а.

Лежат ли эти прямые в одной плоскости?

В пространстве даны прямая а и точка А, принадлежащая ей?

В пространстве даны прямая а и точка А, принадлежащая ей.

Сколько можно провести через точку А прямых, перпендикулярных прямой а?

1)одну 2)две 3)ни одной 4)бесконечно много.

Помогите пожалуйста34?

A) Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну.

B) В любом треугольнике каждая сторона больше суммы двух других сторон.

C) Если две различные прямые имеют общую точку, то через них можно провести множество плоскостей.

D) Через четыре точки не лежащие на одной прямой можно провести плоскость и притом только одну.

Прямые в пространстве параллельны если они лежат в одной плоскости и имеют две общие точки

b) Через точку пространства можно провести прямую параллельную данной и при том только одну.

C) Если две параллельные прямые пересекают третью, то все они параллельны

d) Если две прямые не пересекаются и не лежат в одной плоскости, то они скрещивающиеся.

Прямая и плоскость называются параллельными, если они имеют две общие точки.

C) Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей не параллельна данной прямой.

D) Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая пересекает эту плоскость.

B) Если две параллельные плоскости пересечены третьей, то линии пересечения параллельны

c) Отрезки параллельных прямых заключенных между параллельными плоскостями пересекаются.

D) Две плоскости называются параллельными если они имеют общие точки.

38. Если одна из двух параллельных прямых перпендикулярна к третьей, то другая прямая

Перпендикулярна этой прямой

b) Параллельна этой прямой

Скрещивается с этой прямой

d) Не возможно определить.

39. Если две прямые перпендикулярны к плоскости, то они между собой :

Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости

Пересекаются под острым углом

Расстояние между параллельными плоскостями в пространстве измеряют по

b) По проекции наклонной

d) Неважно как измерять.

Геометрия, тест с вариантами ответа?

Геометрия, тест с вариантами ответа.

1) Две прямые в пространстве могут быть : а) перпендикулярными.

Е) продолжением одна другой.

Б) не имеют общих точек.

В) не имеют общих прямых.

Б) имеют одну общую прямую.

В) имеют две общие точки.

4) Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и а) любой прямой этой плоскости.

Б) ее проекцией на эту плоскость.

В) прямой плоскости, проходящей через основание наклонной.

5) Выберите единственно правильный вариант определения расстояния между скрещивающимися прямыми.

Расстоянием между скрещивающимися прямыми называется а) длина отрезка, соединяющего точки прямых.

Б) расстояние между прямой, лежащей в плоскости, и точкой пересечения другой прямой с данной плоскостью.

В) расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой.

Верно или не верно?

Верно или не верно.

1. Через любую точку плоскости можно провести прям?

2. Через любые две различные точки плоскости можно провести прямую?

3. Через любые три различные точки плоскости можно провести прямую?

4. Любые две различные прямые проходят через одну общую точку?

Могут ли прямая и плоскость иметь одну общую точку?

Могут ли прямая и плоскость иметь одну общую точку?

Скольполос костей можно провести через Три точки?

Сколько плоскостей можно провести через прямую и не лежащую на ней точку?

Могут ли прямая и плоскость иметь одну общую точку?

Источник

Прямая на плоскости – необходимые сведения

Статья рассказывает о понятии прямой на плоскости. Рассмотрим основные термины и их обозначения. Поработаем со взаимным расположением прямой и точки и двух прямых на плоскости. Поговорим об аксиомах. В итоге обсудим методы и способы задания прямой на плоскости.

Прямая на плоскости – понятие

Для начала необходимо иметь четкое представление о том, что такое плоскость. Любую поверхность чего-либо можно отнести к плоскости, только от предметов она отличается своей безграничностью. Если представить, что плоскость – это стол, то в нашем случае он не будет иметь границ, а будет бесконечно огромен.

Если карандашом дотронуться до стола, останется отметина, которую можно называть «точкой». Таким образом, получим представление о точке на плоскости.

Рассмотрим понятие прямой линии на плоскости. Если провести прямую на листе, то она отобразится на нем с ограниченной длиной. Мы получили не всю прямую, а только ее часть, так как на самом деле она не имеет конца, как и плоскость. Поэтому изображение прямых и плоскостей в тетради формальное.

Взаимное расположение прямой и точки

На каждой прямой и в каждой плоскости могут быть отмечены точки.

Для точки и прямой известны только два варианта расположения: точка на прямой, иначе говоря, что прямая проходит через нее, или точка не на прямой, то есть прямая не проходит через нее.

Через любые две точки, находящиеся в любых плоскостях, существует единственная прямая, которая проходит через них.

Прямая, расположенная на плоскости, имеет большое количество точек. Отсюда исходит аксиома:

Если две точки прямой лежат в плоскости, то и все остальные точки данной прямой принадлежат плоскости.

Множество точек, находящееся между двумя заданными, называют отрезком прямой. Он имеет начало и конец. Введено обозначение двумя буквами.

Точка делит прямую на две части, называемые лучами. Имеем аксиому:

Взаимное расположение прямых на плоскости

Расположение прямых на плоскости может принимать вид двух состояний.

Две прямые на плоскости могут совпадать.

Такая возможность появляется, когда прямые имеют общие точки. Исходя из аксиомы, написанной выше, имеем, что через две точки проходит прямая и только одна. Значит, что при прохождении 2 прямых через заданные 2 точки, они совпадают.

Две прямые на плоскости могут пересекаться.

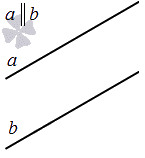
Две прямые на плоскости могут быть параллельны.

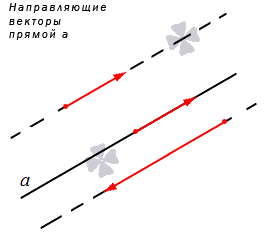
Прямая на плоскости рассматривается вместе с векторами. Особое значение придается нулевым векторам, которые лежат на данной прямой или на любой из параллельных прямых, имеют название направляющие векторы прямой. Рассмотрим рисунок, расположенный ниже.

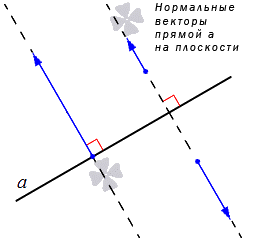
Ненулевые векторы, расположенные на прямых, перпендикулярных данной, иначе называют нормальными векторами прямой. Подробно имеется описание в статье нормальный вектор прямой на плоскости. Рассмотрим рисунок ниже.

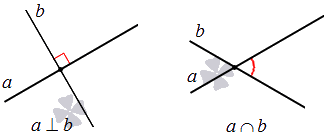
Если на плоскости даны 3 линии, их расположение может быть самое разное. Есть несколько вариантов их расположения: пересечение всех, параллельность или наличие разных точек пересечения. На рисунке показано перпендикулярное пересечение двух прямых относительно одной.

Для этого приводим необходимы факторы, доказывающие их взаимное расположение:

Рассмотрим это на рисунках.

Способы задания прямой на плоскости

Прямая на плоскости может быть задана несколькими способами. Все зависит от условия задачи и на чем будет основано ее решение. Эти знания способны помочь для практического расположения прямых.

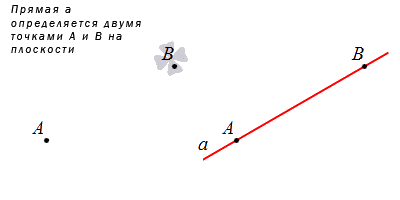
Прямая задается при помощи указанных двух точек, расположенных в плоскости.

Из рассмотренной аксиомы следует, что через две точки можно провести прямую и притом только одну единственную. Когда прямоугольная система координат указывает координаты двух несовпадающих точек, тогда можно зафиксировать уравнение прямой, проходящей через две заданные точки. Рассмотрим рисунок, где имеем прямую, проходящую через две точки.

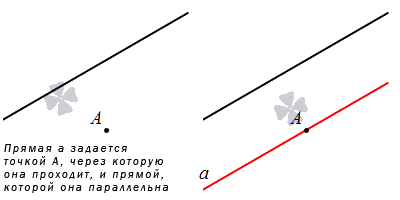
Прямая может быть задана через точку и прямую, которой она параллельна.

Данный способ имеет место на существование, так как через точку можно провести прямую, параллельную заданной, причем, только одну. Доказательство известно еще из школьного курса по геометрии.

Если прямая задана относительно декартовой системы координат, тогда возможно составление уравнения прямой, проходящей через заданную точку параллельно заданной прямой. Рассмотрим принцип задания прямой на плоскости.

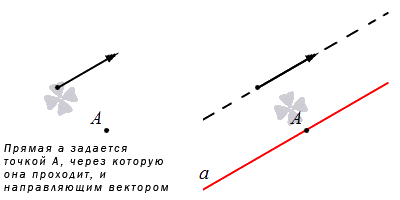
Прямая задается через указанную точку и направляющий вектор.

Когда прямая задается в прямоугольной системе координат, есть возможность составления канонического и параметрического уравнений на плоскости. Рассмотрим на рисунке расположение прямой при наличии направляющего вектора.

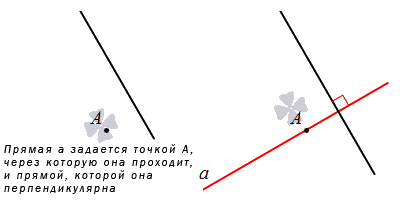
Четвертым пунктом задания прямой имеет смысл, когда указана точка, через которую ее следует начертить, и прямая, перпендикулярная ей. Из аксиомы имеем:

Через заданную точку, расположенную на плоскости, пройдет только одна прямая, перпендикулярная заданной.

И последний пункт, относящийся к заданию прямой на плоскости, это при указанной точке, через которую проходит прямая, и при наличии нормального вектора прямой. При известных координатах точки, которая расположена на заданной прямой, и координатах нормального вектора есть возможность записывания общего уравнения прямой.

Источник