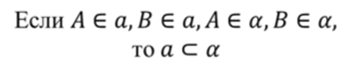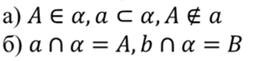Если прямые имеют общую точку то говорят что эти прямые

Пересекающиеся прямые

Если две прямые имеют общую точку, то говорят, что эти прямые пересекаются. Такие прямые называют пересекающимися прямыми:

Точка пересечения — это точка, общая для двух или более геометрических фигур.

Перпендикуляр и наклонная

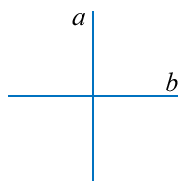
При пересечении вертикальной и горизонтальной прямой линии образуется четыре прямых угла. Такие линии, относительно друг к другу, называются перпендикулярными линиями или просто перпендикулярами:

Даже если прямые не являются вертикальной и горизонтальной линиями, но при пересечении образуют четыре прямых угла, то они всё равно являются перпендикулярными:

Если прямая линия пересекает другую не под прямым углом, то такая линия называется наклонной к прямой, которую она пересекает. При этом образуется четыре угла: два из них будут острыми и два тупыми:

Образованные острые углы равны и относительно друг друга будут называться вертикальными углами. То же самое можно сказать и об образованных тупых углах — они равные и вертикальные.

Источник

Точки, Прямые и Отрезки — Определения и Свойства

Вспомним определения точки и прямой:

Точка — это фигура в геометрии, не имеющая никаких
измеримых характеристик, кроме координат.

Прямая — это фигура в геометрии, которая не
имеет ни начала, ни конца.

Для изображения прямых на чертеже используют линейку, но
при этом можно изобразить только часть прямой, а вся прямая бесконечна.
Принято обозначать прямые малыми латинскими буквами, а точки —
большими латинскими буквами.

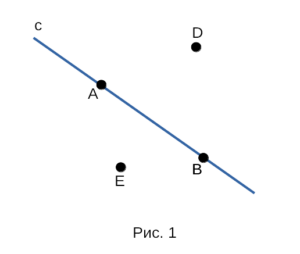
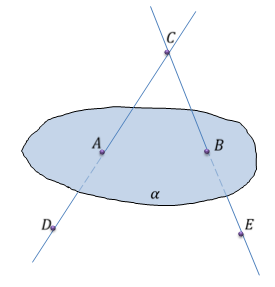
На рисунке 1 изображены прямая c и точки A, B, D, E. Точки А и B
лежат на прямой c, а точки D и E не лежат. Прямая с проходит через
точки A и B, но не проходит через точки С и D. Также заметим, что через
точки A и В нельзя провести другую прямую, не совпадающую с прямой c.

Через любые две точки можно провести прямую,
и притом только одну.

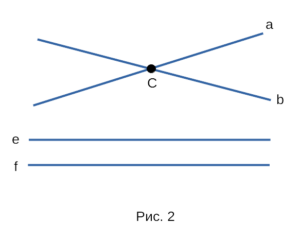
Если две прямые имеют общую точку, то можно сказать,
что они пересекаются. На рисунке 2 прямые a и b
пересекаются в общей точке C, а прямые e и f не
пересекаются, так как не имеют общей точки. Две прямые
не могут иметь двух и более общих точек, так как через две
и более точек проходит только одна прямая.

Две прямые имеют только одну общую точку,
либо не имеют общих точек.

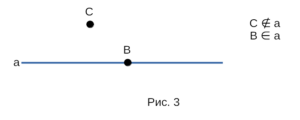
Прямую, на которой отмечены две точки, иногда обозначают двумя
буквами. Для обозначения того, лежит ли точка на прямой или нет,
используют математический символ ∈ или ∉. Пример использования
математического символа ∈ или ∉ на рисунке 3.

Часть прямой ограниченная двумя точками называется отрезком. Точки,
ограничивающие отрезок, называются концами отрезка. Отрезок имеет
начало и конец. Пример отрезка на рисунке 4.

Источник

Если прямые имеют общую точку то говорят что эти прямые

10 класс

Материалы к зачетной работе по теме
«Основные понятия и аксиомы стереометрии. Параллельность прямых и плоскостей»

Стереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве.

Слово «стереометрия» происходит от греческих слов «στερεοσ» — объемный, пространственный и «μετρεο» — измерять.

Простейшие фигуры в пространстве: точка, прямая, плоскость.

Аксиомы стереометрии и их следствия

Аксиома 2.
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. (Прямая лежит на плоскости или плоскость проходит через прямую).

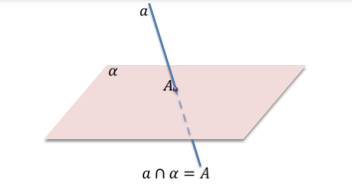
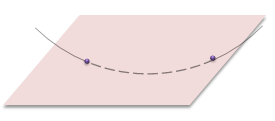
Из аксиомы 2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются.

Аксиома 3.
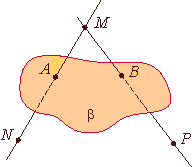
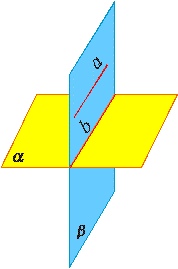
Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

В таком случае говорят, плоскости пересекаются по прямой.

Пример: пересечение двух смежных стен, стены и потолка комнаты.

Некоторые следствия из аксиом

Теорема 2.
Через две пересекающиеся прямые a и b проходит плоскость, и при том только одна.

Параллельные прямые в пространстве

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Теорема о параллельных прямых.

Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

Лемма о пересечении плоскости параллельными прямыми.

Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

Теорема о трех прямых в пространстве.

Если две прямые параллельны третьей прямой, то они параллельны (если a∥c и b∥c, то a∥b).

Параллельность прямой и плоскости

Прямая и плоскость называются параллельными, если они не имеют общих точек.

Признак параллельности прямой и плоскости

Теорема.
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

Теорема.
Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

Теорема.
Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.

Взаимное расположение прямых в пространстве

Пересекающиеся прямые:
лежат в одной плоскости, имеют одну общую точку.

Параллельные прямые:
лежат в одной плоскости, не имеют общих точек (не пересекаются)

Скрещивающиеся прямые:
не лежат в одной плоскости, не имеют общих точек (не пересекаются)

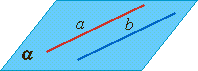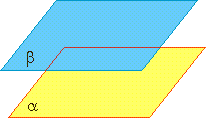Признак параллельности двух плоскостей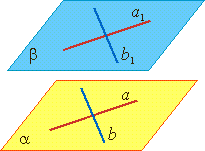

Свойства параллельных плоскостей

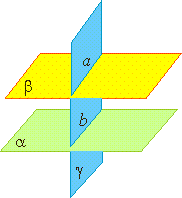
Вели α∥β и они пересекаются с γ, то а∥b.

Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.

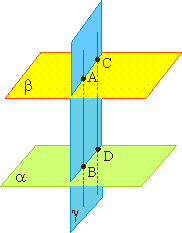
Если α∥β и AB∥CD, то АВ = CD.

Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.

Источник

Аксиомы стереометрии

Урок 2. Геометрия 10 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Аксиомы стереометрии»

На прошлом уроке мы познакомились с разделом геометрии – cтереометрия. Мы сказали, что основными фигурами стереометрии являются точка, прямая и плоскость. Мы вспомнили, как обозначаются точки, прямые, плоскости. Давайте еще раз повторим, что точки обозначаются заглавными буквами латинского алфавита, прямые обозначаются строчными буквами латинского алфавита, плоскости обозначаются строчными буквами греческого алфавита. Плоскость может изображаться разными способами, но чаще всего она изображается параллелограммом. Представление о плоскости дают нам ровные поверхности, например, лист бумаги или школьная доска.

Как правило, такие предметы имеют прямоугольную форму, но если посмотреть на эти предметы под углом и на большом расстоянии, то они покажутся нам параллелограммами. Поэтому чаще всего, плоскости изображают параллелограммами или просто в виде произвольной области.

Сразу оговоримся, что хоть плоскость и изображается параллелограммом, но она понимается неограниченной во все стороны.

Очевидно, что в любой плоскости лежат какие-то точки пространства, но не все точки пространства лежат в одной и той же плоскости.

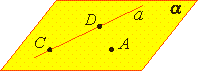
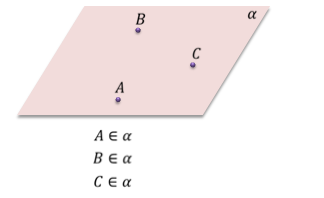
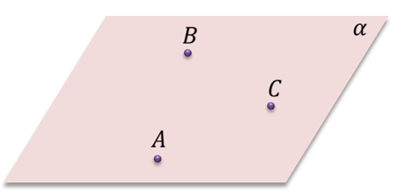
Например, на нашем рисунке изображена плоскость и несколько точек.

Легко заметить, что точки A и B лежат на плоскости α, а точки C, D, E – не лежат на этой плоскости. Математически это можно записать так:

Когда мы с вами начинали изучать планиметрию, мы начинали с аксиом планиметрии. Напомним, что аксиома – утверждение, не требующее доказательства. В аксиомах стереометрии выражаются основные свойства точек, прямых и плоскостей, которые касаются их взаимного расположения.

Прежде всего, давайте определим, сколько точек надо взять, чтобы плоскость задавалась однозначно. Если мы возьмем одну точку, то через нее можно провести не менее двух плоскостей, то есть одна точка не задает однозначно плоскость.

Возьмем две точки. Согласно аксиомам планиметрии, через две точки можно провести прямую и притом только одну, то есть две точки однозначно задают только прямую. Через эту прямую можно провести не менее двух плоскостей, то есть и две точки не задают однозначно плоскость.

Теперь давайте посмотрим на дверь. Она крепится к стене с помощью петель. И относительно петель поворачивается. Если петли обозначить точками и провести через них прямую, а полотно двери обозначить за плоскость, то получим, что плоскость поворачивается относительно прямой. Теперь давайте дверную ручку обозначим за точку, тогда получим, что прямая и одна точка задают плоскость, причем однозначно. То есть плоскость однозначно задается тремя точками. Об этом и говорит первая аксиома.

Итак, сформулируем первую аксиому. Для удобства аксиомы мы будем обозначать большой буквой А с нижним индексом, который будет обозначать номер аксиомы.

A1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

Давайте теперь схематично изобразим эту аксиому. Отметим произвольные точки A, B, C, которые не лежат на одной прямой, и проведем плоскость α.

Тогда можно записать, что каждая из этих точек принадлежит плоскости α. Аксиома утверждает, что такая плоскость единственная.

Примером этой аксиомы может служить детский велосипед с тремя колесами. Если мы обозначим место соприкасания колес с дорожкой точкой, то получим три точки, которые задают плоскость дорожки. Благодаря этому трехколесный велосипед устойчиво стоит на дорожке.

Перейдем ко второй аксиоме.

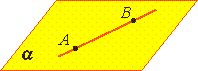
A₂. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. Тогда говорят, что прямая лежит в плоскости или плоскость проходит через прямую.

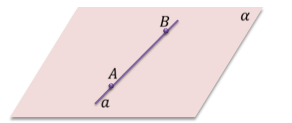
Схематически аксиому можно изобразить так. Изобразим точки Aи B и проведем через них прямую a и плоскость α.

Тогда можно записать, что если точки A и B принадлежат прямой a и плоскости α, то прямая a лежит в плоскости α. Записывается это так:

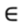
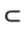
Давайте сразу определимся в каком случае какой символ принадлежности надо писать. Если речь идет о принадлежности точки чему-то, то пишем такой символ. Если мы говорим о принадлежности прямой чему-то, то тогда надо писать такой символ.

Вторую аксиому можно использовать для проверки ровности стола. Для этого надо взять линейку и приложить ее краем к поверхности стола, если поверхность стола ровная, то просветов между линейкой и столом не будет, а если поверхность стола не совсем ровная, то будут зазоры между линейкой и столом.

Из этой аксиомы следует:

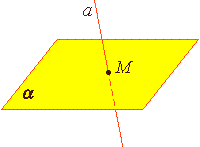
Если прямая не лежит в плоскости, то она может иметь с плоскостью не более одной общей точки.

Покажем это на чертеже. Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются.

Перейдем к следующей аксиоме.

A₃. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. Если плоскости имеют общую точку, то они пересекаются по прямой, содержащей эту точку.

Сделаем схематический рисунок этой аксиомы.

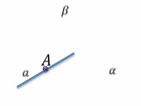
Пусть нам дана точка А и две плоскости, которые проходят через эту точку. Обозначим эти плоскости за α и β. Запишем, что если А принадлежит плоскостям α и β, то плоскости α и β пересекаются по прямой a.

Примеров этой аксиомы очень много. Например, обыкновенная открытка (здесь плоскостями будут части открытки, а линия сгиба – линией их пересечения) или стены в комнате (здесь сами стены будут плоскостями, а линия их соединения – линией их пересечения).

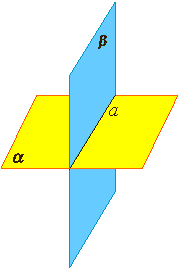
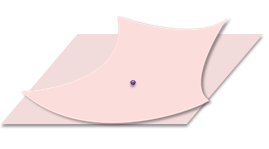
Вторая и третья аксиомы говорят о расположении прямых и плоскостей в пространстве. Кроме того, они выражают свойство не искривлённости прямой и плоскости. Две плоскости не могут располагаться как на рисунке, а прямая не может отклоняться от плоскости.

Отметим, что все аксиомы и утверждения планиметрии справедливы в стереометрии на каждой плоскости пространства.

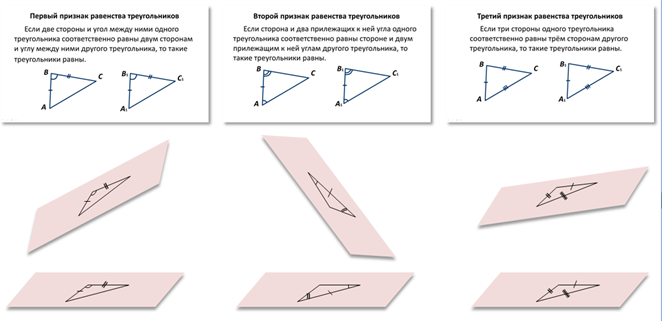
Например, признаки равенства треугольников, которые мы изучали в планиметрии, справедливы и для треугольников, которые расположены в разных плоскостях.

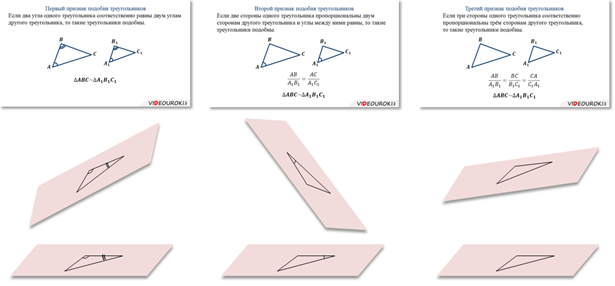
Аналогично для треугольников, которые расположены в разных плоскостях, справедливы признаки подобия

Сейчас давайте рассмотрим обозначения, которые будут использоваться при решении задач и доказательстве теорем.

На чертеже видно, что точка А лежит на прямой a. ЗаписываетсяЧитается так: точка А принадлежит прямой a или другими словами, прямая aпроходит (или проведена) через точку А.

Точка B не принадлежит прямой А. Записывается 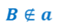Читается: точка B не принадлежит прямой a или, другими словами, прямая a не проходит (или не проведена) через точку B.

Теперь давайте запишем как располагаются точки А и B относительно плоскости α. Записывается это точно так же как и в случае точек и прямой a, но при прочтении слово прямой заменяется словом плоскости.

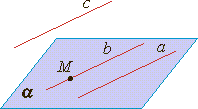
Теперь давайте посмотрим на расположение прямых и плоскости. Прямая a лежит в плоскости α. Записывается это так Читается: прямая aпринадлежит плоскости α или другими словами плоскость α проходит (проведена) через прямую a.

Прямая b не лежит в плоскости α. Записывается это так 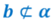Читается: прямая b не принадлежит плоскости α или другими словами плоскость α не проходит (не проведена) через прямую b.

Теперь рассмотрим взаимное расположение прямыхa и b. Эти прямые пересекаются. Записывается это так 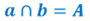Читается: прямая a пересекает прямую b в точке А.

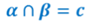
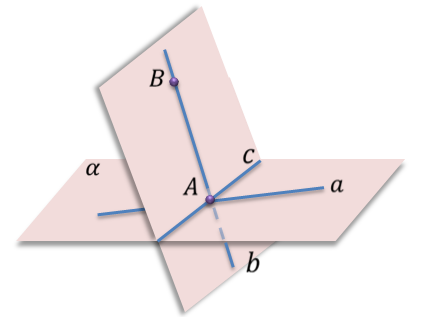
Давайте построим еще одну плоскость β. Очевидно, что α и β пересекаются. Записывается это так Читается: плоскость альфа пересекает плоскость β по прямой c.

Выполним задание. Прочитать записи и сделать схематический рисунок.

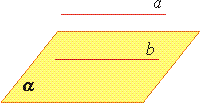
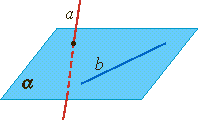
В первом случае прочитать записи можно так: плоскость α проходит через точку А и прямую a, но точка А не принадлежит прямой a.

Сделаем схематичный рисунок. Изобразим плоскость α и отметим на ней прямую a и точку А так, чтобы точка А не лежала на прямой a.

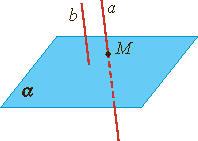
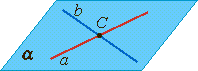
Во втором случае прочитать записи можно так: прямая a пересекает плоскость α в точке А, прямая b пересекает плоскость α в точке В.

Сделаем схематичный рисунок. Изобразим плоскость альфа и проведем прямые a и b так, чтобы они пересекали плоскость α соответственно в точках А и B.

Мы знаем, что помимо строчных букв латинского алфавита прямые могут обозначаться двумя заглавными буквами, которые соответствуют точкам, лежащим на прямой. Аналогично и плоскости могут называться тремя заглавными буквами латинского алфавита, которые соответствуют точкам, которые задают плоскость. Например, плоскость на рисунке можно назвать плоскость альфа или плоскость ABC.

Решим еще одну задачу.

Подведем итоги урока. Сегодня на уроке мы сформулировали основные аксиомы стереометрии. Показали, как записываются и читаются некоторые математические символы.

Источник

§ 1. Прямая и отрезок

Точки, прямые, отрезки

В этой главе речь пойдёт о простейших геометрических фигурах-точках, прямых, отрезках, лучах, углах. С ними вы познакомились на уроках математики в 5 и 6 классах. К тому, что вы знаете об этих фигурах, мы добавим новые сведения, и они послужат нам опорой для изучения в следующих главах свойств более сложных фигур. Ещё мы расскажем о практических приложениях геометрии —о том, как геометрия помогает прокладывать прямолинейные дороги и как проводится измерение углов на местности.

Вспомним, что нам известно о точках и прямых. Мы знаем, что для изображения прямых на чертеже пользуются линейкой (рис. 4), но при этом можно изобразить лишь часть прямой, а всю прямую мы представляем себе простирающейся бесконечно в обе стороны.

Обычно прямые обозначают малыми латинскими буквами, а точки — большими латинскими буквами. На рисунке 5 изображены прямая а и точки А, В, С и D. Точки А и В лежат на прямой а, а точки С и D не лежат на этой прямой. Можно сказать, что прямая а проходит через точки А и В, но не проходит через точки С и В. Отметим, что через точки А и В нельзя провести другую прямую, не совпадающую с прямой а.

Рассмотрим теперь две прямые. Если они имеют общую точку, то говорят, что эти прямые пересекаются. На рисунке 6 прямые а и b пересекаются в точке О, а прямые р и q не пересекаются. Две прямые не могут иметь двух и более общих точек. В самом деле, если бы две прямые имели две общие точки, то каждая из прямых проходила бы через эти точки. Но через две точки проходит только одна прямая. Таким образом, можно сделать вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Прямую, на которой отмечены две точки, например А и В, иногда обозначают двумя буквами: АВ или ВА. Для краткости вместо слов «точка А лежит на прямой а» используют запись А ∈ а, а вместо слов «точка В не лежит на прямой а» — запись В ∉ а.

На рисунке 7, а выделена часть прямой, ограниченная двумя точками. Такая часть прямой называется отрезком. Точки, ограничивающие отрезок, называются его концами. На рисунке 7, б изображён отрезок с концами А и В. Такой отрезок обозначается АВ или В А. Отрезок АВ содержит точки А и В и все точки прямой АВ, лежащие между А и В.

Провешивание прямой на местности

Решим такую задачу: с помощью данной линейки построить отрезок более длинный, чем сама линейка. С этой целью приложим к листу бумаги линейку, отметим точки А и В и какую-нибудь точку С, лежащую между А к В (рис. 8, а). Затем передвинем линейку вправо так, чтобы её левый конец оказался около точки С, и отметим точку D около правого конца линейки (рис. 8, б). Точки А, В, С и D лежат на одной прямой. Если мы проведём теперь отрезок АВ, а затем отрезок BD, то получим отрезок AD, более длинный, чем линейка.

Аналогичный приём используется для «проведения» длинных отрезков прямых на местности. Этот приём заключается в следующем. Сначала отмечают какие-нибудь точки А и В. Для этой цели используют две вехи — шесты длиной около 2 м, заострённые на одном конце для того, чтобы их можно было воткнуть в землю. Третью веху ставят так, чтобы вехи, стоящие в точках А и В, закрывали её от наблюдателя, находящегося в точке А (точка С на рисунке 9). Следующую веху ставят так, чтобы её закрывали вехи, стоящие в точках В и С, и т. д.

Описанный приём называется провешиванием прямой (от слова «веха»). Он широко используется на практике, например при рубке лесных просек, при прокладывании шоссейных или железных дорог, линий высоковольтных передач и т. д.

Практические задания

1. Проведите прямую, обозначьте её буквой а и отметьте точки А и В, лежащие на этой прямой, и точки Р, Q и R, не лежащие на ней. Опишите взаимное расположение точек А, В, Р, Q, R и прямой а, используя символы ∉ и ∈.

2. Отметьте три точки А, В и С, не лежащие на одной прямой, и проведите прямые АВ, ВС и СА.

3. Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.

4. Отметьте точки А, В, С, D так, чтобы точки А, В, С лежали на одной прямой, а точка D не лежала на ней. Через каждые две точки проведите прямую. Сколько получилось прямых?

5. Проведите прямую а и отметьте на ней точки А и В. Отметьте: а) точки М и N, лежащие на отрезке АВ; б) точки Р и Q, лежащие на прямой а, но не лежащие на отрезке АВ; в) точки R и S, не лежащие на прямой а.

6. Проведите прямую и отметьте на ней три точки. Сколько отрезков получилось на прямой?

7. На рисунке 10 изображена прямая, на ней отмечены точки А, В, С и D. Назовите все отрезки: а) на которых лежит точка С; б) на которых не лежит точка В.

Источник