Если тогда чему равно выражение n

Числовая последовательность

Определение 1. Числовой последовательностью называется функция, аргументом которой является множество всех натуральных чисел, или множество первых n натуральных чисел.

Обозначается числовая последовательность так:

где −i-ый член последовательности.

При словестном задании последовательности, описывается из каких элементов она состоит.

Последовательность нечетных чисел:

Последовательность простых чисел :

Последовательности (1) и (2) мы задали словестно.

Последовательность нечетных чисел аналитически задается формулой

Отметим, что последовательность простых чисел невозможно задать аналитически.

Пример задания рекуррентной последовательности:

В этой последовательности

Пример стационарной последовательности:

Возрастающие и убывающие последовательности

Определение 3. Последовательность, в которой каждый последующий член (кроме первого) больше предыдующего, называется возрастающей :

Определение 4. Последовательность, в которой каждый последующий член (кроме первого) меньше предыдующего, называется убывающей :

Пример 1. Выяснить, монотонна ли последовательность

Решение. Запишем n+1 член последовательности (подставим вместо n, n+1):

Найдем разность членов и :

.

(3)

Так как n=1,2,3. то правая часть уравнения (3) положительна. Тогда:

Таким образом, каждый последующий член последовательности больше предыдующего. Следовательно последовательность является возрастающим (и монотонным).

Пример 2. Выяснить, при каких значениях a последовательность (b_n) является возрастающей и при каких, убывающей:

Решение. Запишем n+1 член последовательности (вместо n подставим n+1):

Найдем разность членов и :

(4)

Посмотрим на правую часть выражения (4). Если a 10, то . Тогда последовательность является убывающей. При a=10 . Последовательность имеет одинаковые члены:

т.е. имеем дело с последовательностью

Очевидно, что последовательность (5) не является монотонной. Она является стационарной последовательностью.

Ограниченные и неограниченные последовательности

Определение 5. Последовательность (y_n) называется ограниченной сверху, если существует такое число k, что y_n Определение 6. Последовательность (y_n) называется ограниченной снизу, если существует такое число k, что y_n>k при любом n.

Определение 7. Последовательность (y_n) называется ограниченной, если она ограничена и сверху, и снизу.

Пример 3. Показать, что последовательность (a_n) является монотоннной и ограниченной:

Решение. Запишем n+1 член последовательности (вместо n подставим n+1):

Найдем разность членов и :

(6)

Правая часть равенства (6) положительна при любых натуральных чисел n. Следовательно последовательно (a_n) возрастающая (и монотонная).

Далее, сделаем эквивалентное преобразование для проследовательности (5):

Из выражения (7) видно, что при любых n a_n≤1. Т.е. хотя последовательность возрастает, то остается меньше числа 1 (ограничена сверху). Запишем несколько членов данной последовательности, задав n=1,2,3.

Так как последовательность возрастающая, то все члены последовательности не меньше . Тогда последовательность ограничена также и снизу. Таким образом последовательность ограничена и всерху, и снизу, т.е. является ограниченной последовательностью.

Сходящиеся и расходящиеся последовательности

Рассмотрим две числовые последовательности:

На координатной прямой изобразим члены этих последовательностей:

Предел числовой последовательности

Точка, к которой приближаются члены последовательности при увеличении n, называется пределом последовательности. Для последовательности (10) пределом является число 0. Более строго предел последовательности определяется так:

Определение 8. Число k называют пределом последовательности (y_n), если для любой заранее выбранной окресности точки k, можно выбрать такой номер n₀, чтобы все члены последовательности, начиная с номера n₀ содержались в указанной окрестности.

Если k является пределом последовательности (y_n), то пишут ( стремится к k или сходится к k).

Обозначают это так:

Выраженние (11) читается так: предел проследовательности , при стремлении n к бесконечности равен k.

Изложим некоторые пояснения к определению 8.

Пусть выполнено (11). Возьмем окрестность точки k, т.е. интервал , где радиус этой окрестности ( >0). По определению, существует номер n₀, начиная с которого вся последовательность содержится в указанной окресности, т.е.

.

Если же взять другую окресность (пусть ), то найдется другой номер n₁, начиная с которого, вся последовательность содержится в указанной окрестности, но этот номер будет больше n₁ > n₀.

Пример 4. Дана полследовательность (y_n):

Доказать, что .

Решение. Найдем любую окрестность точки 0. Пусть ее радиус равен r. Тогда всегда можно выбирать n₀ так, чтобы .

Пусть, например, r=0.001. Вычислим n‘ из уравнения

.

В качестве n₀ берем 501. Имеем:

.

Запишем члены последовательности (12) начиная с номера 501:

.

Далее, учитывая (13), имеем:

.

Следовательно, все члены последовательности (12) начиная с номера 501 попадают в окресность . А по определению 8, это означает:

Пример 5. Дана полследовательность (y_n):

Доказать, что .

Решение. Найдем любую окрестность точки 2. Пусть ее радиус равен r. Тогда всегда можно выбирать n₀ так, чтобы

.

.

Неравенство в (17) всегда выполняется так как n₀ натуральное число, а правая часть неравенства отрицательно (это означает, что для любого n₀). Из неравенства (16) можно найти номер n₀, начиная с которого члены последовательности попадают в окресность (2−r; 2+r). Например, пусть r=0.001, тогда . Тогда нужно брать n₀=2000. И тогда все члены последовательности, начиная с номера 2000 попадают в окрестность (2−r; 2+r).

Запишем члены последовательности, начиная с номера 2000:

.

Легко проверить, что . Тогда, учитывая, что данная последовательность возрастающая (см. пример 1), получим:

.

Пример 6. Найти предел последовательности

Решение. Выполним некоторые преобразования выражения (18):

Тогда последовательность (18) можно переписать так:

(19)

Как видно из (19), пройдя по членам последовательности слева направо, из числа 1 вычитается все меньшее и меньшее положительное число. Т.е. последовательность приближается к числу 1. Тогда 1 является пределом последовательности (19) и (18):

Свойства сходящихся последовательностей

Сходящиеся последовательности обладают рядом свойств.

Свойство 1. Если последовательность сходится, то только к одному пределу.

Свойство 2. Если последовательность сходится, то она ограничена.

Свойство 3. Если последовательность монотонна и ограничена, то она сходится (теорема Вейерштрасса).

Предел стационарной последовательности равен значению любого члена последовательности:.

Теорема. Если , то

1. Предел суммы равен сумме пределов:

2. Предел произведения равен произведению пределов:

3. Предел частного равен частному пределов:

4. Постоянный множитель можно вывести за знак предела:

Пример 7. Найти предел последовательности:

Решение. Так как , то

.

Пример 8. Найти предел последовательности:

Решение. Применив правило «предел суммы» теоремы, получим

.

Пример 9. Вычислить:

Решение. Делим числитель и знаменатель дроби на наивысшую из имеющихся степень переменного n. Далее используем правило «предел суммы» для числителя и знаменателя и правило «предел частного»:

Источник

ЕСЛИ (функция ЕСЛИ)

Функция ЕСЛИ — одна из самых популярных функций в Excel. Она позволяет выполнять логические сравнения значений и ожидаемых результатов.

Поэтому у функции ЕСЛИ возможны два результата. Первый результат возвращается в случае, если сравнение истинно, второй — если сравнение ложно.

Например, функция =ЕСЛИ(C2=»Да»;1;2) означает следующее: ЕСЛИ(С2=»Да», то вернуть 1, в противном случае вернуть 2).

Функция ЕСЛИ, одна из логических функций, служит для возвращения разных значений в зависимости от того, соблюдается ли условие.

ЕСЛИ(лог_выражение; значение_если_истина; [значение_если_ложь])

Условие, которое нужно проверить.

Значение, которое должно возвращаться, если лог_выражение имеет значение ИСТИНА.

Значение, которое должно возвращаться, если лог_выражение имеет значение ЛОЖЬ.

Простые примеры функции ЕСЛИ

В примере выше ячейка D2 содержит формулу: ЕСЛИ(C2 = Да, то вернуть 1, в противном случае вернуть 2)

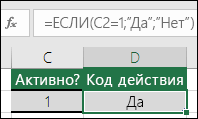
В этом примере ячейка D2 содержит формулу: ЕСЛИ(C2 = 1, то вернуть текст «Да», в противном случае вернуть текст «Нет»). Как видите, функцию ЕСЛИ можно использовать для сравнения и текста, и значений. А еще с ее помощью можно оценивать ошибки. Вы можете не только проверять, равно ли одно значение другому, возвращая один результат, но и использовать математические операторы и выполнять дополнительные вычисления в зависимости от условий. Для выполнения нескольких сравнений можно использовать несколько вложенных функций ЕСЛИ.

B2;»Превышение бюджета»,»В пределах бюджета»)» loading=»lazy»>

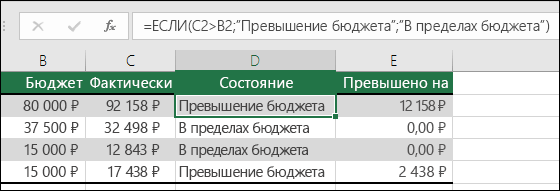
=ЕСЛИ(C2>B2;»Превышение бюджета»;»В пределах бюджета»)

В примере выше функция ЕСЛИ в ячейке D2 означает: ЕСЛИ(C2 больше B2, то вернуть текст «Превышение бюджета», в противном случае вернуть текст «В пределах бюджета»)

B2;C2-B2;»»)» loading=»lazy»>

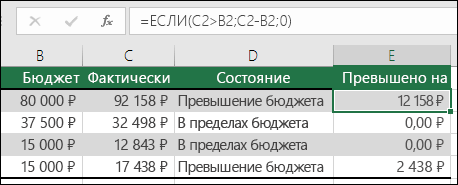
На рисунке выше мы возвращаем не текст, а результат математического вычисления. Формула в ячейке E2 означает: ЕСЛИ(значение «Фактические» больше значения «Плановые», то вычесть сумму «Плановые» из суммы «Фактические», в противном случае ничего не возвращать).

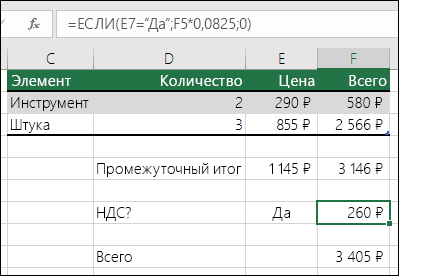
В этом примере формула в ячейке F7 означает: ЕСЛИ(E7 = «Да», то вычислить общую сумму в ячейке F5 и умножить на 8,25 %, в противном случае налога с продажи нет, поэтому вернуть 0)

Примечание: Если вы используете текст в формулах, заключайте его в кавычки (пример: «Текст»). Единственное исключение — слова ИСТИНА и ЛОЖЬ, которые Excel распознает автоматически.

Распространенные неполадки

Не указан аргумент значение_если_истина или значение_если_ложь. Чтобы возвращать правильное значение, добавьте текст двух аргументов или значение ИСТИНА/ЛОЖЬ.

Как правило, это указывает на ошибку в формуле.

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

Источник

Excel-plus

Пошаговые инструкции, как использовать функции, формулы и другие инструменты табличного редактора Microsoft Excel

Функция ЕСЛИ в MS Excel. Описание и примеры использования.

Функция ЕСЛИ в MS Excel. Описание и примеры использования.

В данной статье рассмотрим функцию MS Excel, которая называется ЕСЛИ. Данная функция позволяет проверить, соответствует ли содержащиеся в указанной ячейки данные заданному критерию или нет. В зависимости от результата проверки функция выводит заданное значение. Чтобы понять суть и возможности функции ЕСЛИ, рассмотрим примеры с ее использованием.

Функция ЕСЛИ в MS Excel с одним условием.

Функцией ЕСЛИ в Excel, первый пример.

Рассмотрим простой пример применения функции ЕСЛИ в MS Excel. У нас есть столбец №1, в котором содержаться числа от 1 до 10.

Необходимо проверить, соответствует ли числа находящиеся в столбце №1 нашему критерию. Критерий: является ли числа находящиеся в столбце №1 числами, значения которых больше числа 4.

Взываем функцию ЕСЛИ в ячейку С3.

В диалоговом окне Аргументы функции видим три поля для заполнения:

логическое_выражение — B3>4, здесь указан наш критерий проверки. В данном случае проверяем ячейку В3. Функция определяет, является ли число, которое содержится в этой ячейки, числом больше числа 4.

значение_если_истина — «правда», это слово появиться в ячейки С3, если число содержащиеся в ячейки В3 больше числа 4. То есть выполняется условие заданное в логическом_выражении.

значение_если_ложь — «неправда», это слово появиться в ячейки С3, если число содержащиеся в ячейки В3 меньше числа 4. То есть не выполниться условие заданное в логическом_выражении.

Важно: текст указанный в полях «значение_если_истина» и «значение_если_ложь», должны быть заключены в кавычки. Иначе функция выдаст ошибку.

Нажимаем ОК в диалоговом окне Аргументы функции.

Как видим, число содержащиеся в ячейки В3 не является числом, которое больше числа 4. Функция ЕСЛИ вернула значение_если_ложь (неправда). Протянем функцию ЕСЛИ вниз по столбцу, чтобы проверить значения находящиеся в остальных ячейках столбца №1, на соответствие нашему критерию (логическое_выражение).

Как видно из результата, ячейки в диапазоне В7:В12 содержат в себе числа, которые больше числа 4. Функция ЕСЛИ вернула значение_если_истина (правда).

Функция ЕСЛИ в Excel, второй пример.

Рассмотрим еще один пример. Предположим, что у нас есть таблица. В ней фамилии студентов, которые сдавали зачет. Часть студентов сдали зачет, а часть не сдали.

Теперь добавим в нашу таблицу столбец: Допуск к экзамену. Используем функцию ЕСЛИ для того, чтобы определить допущен студент к экзамену или нет. Диалоговое окно Аргументы функции будет выглядеть вот так:

Важно: текстовый критерий в поле логическое_выражение должен быть заключен в кавычки. Иначе функция выдаст ошибку.

Если студен сдал зачет, он допущен к экзамену, если нет, то не допущен. Нажимаем ОК в диалоговом окне Аргументы функции и протягиваем функцию ЕСЛИ вниз, по всему столбцу Допуск к экзамену. Получаем:

Видим, что в зависимости от результатов сдачи зачета, студент допущен к экзамену, либо не допущен.

Обращаю внимание, что при работе с функцией ЕСЛИ, можно использовать разные варианты равенств: больше (>), меньше( =), меньше или равно ( ).

Функция ЕСЛИ в MS Excel с несколькими условиями.

Предположим, что у нас есть таблица с результатами сдачи контрольной работы студентами ВУЗа. Результаты контрольной работы оцениваются в баллах. От 0 до 100. Где все, что выше 90 баллов, отлично. Выше 80 баллов, это хорошо. Выше 70 баллов, это удовлетворительно. Ниже 70 баллов, это плохо.

Формула функции ЕСЛИ будет выглядеть вот так:

Где ячейка С3, первая из проверяемых ячеек в столбце Оценка. Далее функция протянута вниз по столбцу Результат, до конца таблицы.

Внимание: в данном случае формула функции ЕСЛИ прописана в ручную, прямо в строе формулы.

Таблица выглядит вот так:

В столбце Результат, в зависимости от количества баллов, функция ЕСЛИ вернула значение, согласно заданному критерию в формуле функции.

Использование операторов «И» и «ИЛИ» в функции ЕСЛИ в MS Excel.

Пример функции ЕСЛИ с оператором «И».

У нас есть таблица, в которой три столбца с числами. Проверим, равны ли эти числа между собой, в пределах одной строки. Если числа будут равны между собой, функция ЕСЛИ вернет значение «правда». Если не равны, функция ЕСЛИ вернет значение «неправда».

Формула функции ЕСЛИ выглядит вот так:

Внимание: в данном случае формула функции ЕСЛИ прописана в ручную, прямо в строе формулы.

Сравниваются ячейки В2 с С2, С2 с ячейкой D2 и D2 с ячейкой В2. Только, если все числа в этих ячейках равны между собой, функция возвращает значение «правда». Как видно на примере, только в нижней строке таблицы (строка №4), функция ЕСЛИ вернула значение «правда», так как в этой строке все числа между собой равны.

Пример функции ЕСЛИ с оператором «ИЛИ».

Возьмем туже самую таблицу, но используем оператор «ИЛИ».

Формула функции ЕСЛИ выглядит вот так:

Внимание: в данном случае формула функции ЕСЛИ прописана в ручную, прямо в строе формулы.

Как видно из этого примера, функция ЕСЛИ вернула значение «правда» два раза. В верхней строке таблицы (строка №2) и в нижней строке таблицы (строка №4). Как и в прошлом примере сравнивались ячейки В2 с С2, С2 с ячейкой D2 и D2 с ячейкой В2. Но в данном случае функция ЕСЛИ вернула значение «правда» и в том случае, когда нашла частичное равенство числе в верхней строке таблицы (строка №2). Число в ячейки В2 равно числу в ячейки D2.

Источник