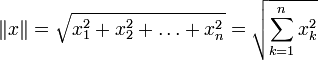Евклидова плоскость что это

18.04.202224.04.2022 admin 0 Comments

Что такое Евклидово пространство?

Если заглянуть в справочники или энциклопедии, то можно найти следующий ответ на сформулированный выше вопрос: «Евклидово пространство – в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии» [1].

Действительно, в АКСИОМЕ 9 Евклид упоминает вскользь слово «пространство» [2]: «И две прямые не содержат пространства».

Фактически же, здесь, как и в во всех прочих аксиомах, речь идёт не о пространстве, а о плоскости, которая является лишь слоем пространства, толщиной в одну точку. Туманную формулировку 9-й аксиомы можно интерпретировать следующим образом [3]: «два отрезка не могут сходиться в двух различных точках – то есть ограничивать некоторую фигуру конечной площади» (см. рисунок слева).

Примечательно, что это единственное (!) упоминание слова «пространство» Евклидом. Больше мы не встретим даже намёка на пространство ни среди других аксиом, ни среди постулатов, ни среди определений его 15-томного труда.

Таким образом, согласно энциклопедиям, ЕВКЛИДОВО ПРОСТРАНСТВО (в изначальном смысле) – это плоскость, которую не содержат две прямые. 🙂

P.S. Из правого рисунка видно, что так называемые «пространства» Евклида, Лобачевского или Римана на самом деле являются лишь поверхностями с разными геометрическими свойствами.

1. Евклидово пространство: Материал из Википедии. – https://ru.wikipedia.org/wiki/Евклидово_пространство

2. Начала Евклида. Книги I-XV. Перевод с греческого и комментарии Д. Д. Мордухай-Болтовского при участии М. Я. Выгодского и И. Н. Веселовского. – Гос. изд-во технико-теоретич. лит-ры, М.-Л.: 1950. – 1299 с.

Источник

Евклидова плоскость

В математике термин евкли́дово простра́нство может обозначать один из сходных и тесно связанных объектов:

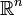
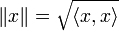
1. Конечномерное вещественное векторное пространство с введённым на нём (положительно определенным) скалярным произведением, порождающим норму:

в простейшем случае (евклидова норма):

где 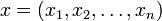(в евклидовом пространстве всегда можно выбрать базис, в котором верен именно этот простейший вариант).

Иначе говоря евклидово пространство — конечномерное гильбертово пространство.

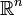
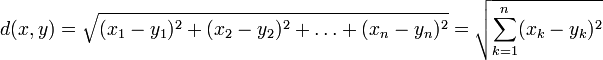
2. Метрическое пространство, которое является конечномерным векторным пространством над полем вещественных чисел с евклидовой метрикой, введённой по формуле:

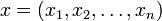
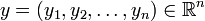
где и , то есть с функцией расстояния, порождаемой описанной выше нормой.

Содержание

Связанные определения

Примеры

Наглядными примерами евклидовых пространств могут служить пространства:

Можно привести и несколько более абстрактные примеры:

Не считается обычно евклидовым физическое 4-мерное пространство-время, т.к. основная метрика на нём, в соответствии с обычным в современной физике взглядом, псевдоевклидова. Хотя при желании евклидовская метрика может быть формально введена на нём тем или иным образом (если не пренебрегать гравитацией — то локально), что бывает иногда полезно, однако она не лоренц-инвариантна, что здесь очень сильно снижает её ценность с точки зрения современной физики.

См. также

Ссылки

Полезное

Смотреть что такое «Евклидова плоскость» в других словарях:

Плоскость Лобачевского — Геометрия Лобачевского (гиперболическая геометрия) одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на… … Википедия

Плоскость (геометрия) — У этого термина существуют и другие значения, см. Плоскость. Сюда перенаправляется запрос «Плоскостность». На эту тему нужна отдельная статья … Википедия

Евклидова геометрия — геометрия, систематическое построение которой было впервые дано в 3 в. до н. э. Евклидом. Система аксиом Е. г. опирается на следующие основные понятия: точка, прямая, плоскость, движение и следующие отношения: «точка лежит на прямой на… … Большая советская энциклопедия

ПЛОСКОСТЬ — одно из основных понятий геометрии; обычно косвенным образом определяется аксиомами геометрии. П. может рассматриваться как совокупность двух непересекающихся множеств множества точек и множества прямых с симметричным отношением инцидентности,… … Математическая энциклопедия

Круговая плоскость — Круговая плоскость евклидова плоскость, дополненная одной идеальной точкой ( ). Ссылки E.F. Assmus Jr and J.D. Key, Designs and their codes, Cambridge University Press, ISBN 0 521 45839 0. с. 309 312. P. Dembowski, Finite geometries,… … Википедия

Проективная плоскость — в первоначальном смысле евклидова плоскость, дополненная бесконечно удаленными точкамии бесконечно удаленной прямой (см. Проективная геометрия). С топологической точки зрения П. п. является замкнутой неориентируемой поверхностью, эйлерова … Большая советская энциклопедия

N-мерная евклидова геометрия — N мерная евклидова геометрия обобщение евклидовой геометрии на пространство большего числа измерений. Хотя физическое пространство является трёхмерным[1], и человеческие органы чувств рассчитаны на восприятие трёх измерений[2], N мерная… … Википедия

Горизонтальная плоскость — Горизонтальная плоскость плоскость, которая в декартовой системе координат перпендикулярна вертикальной оси и параллельна плоскости … Википедия

Проективная геометрия — раздел геометрии, изучающий проективные плоскости и пространства. Главная особенность проективной геометрии состоит в принципе двойственности, который прибавляет изящную симметрию во многие конструкции. Проективная геометрия может изучаться как с … Википедия

Пучёк — Проективная геометрия раздел геометрии, изучающий проективные плоскости и пространства. Главная особенность проективной геометрии состоит в принципе двойственности, который прибавляет изящную симметрию во многие конструкции. Проективная геометрия … Википедия

Источник

Евклидовы пространства

Определение евклидова пространства

0\quad \forall \mathbf\ne \mathbf

\forall \lambda\in \mathbb\,;\\[5pt] &\bold<4.>\quad \langle\mathbf,\mathbf\rangle>0\quad \forall \mathbf\ne \mathbf

Линейные операции над векторами евклидова пространства удовлетворяют аксиомам 1–8 линейного пространства, а операция скалярного умножения векторов удовлетворяет аксиомам 1–4 скалярного произведения. Можно сказать, что евклидово пространство — это вещественное линейное пространство со скалярным произведением. Поскольку евклидово пространство является линейным пространством, на него переносятся все понятия, определенные для линейного пространства, в частности, понятия размерности и базиса.

Простейшие следствия из аксиом скалярного произведения

1. Аксиомы 2 и 3 скалярного произведения можно заменить одним условием линейности скалярного произведения по первому сомножителю:

\forall \alpha,\beta\in \mathbb.[/math]

2. Условие линейности скалярного произведения по первому сомножителю в силу симметричности (аксиома 1) справедливо и для второго сомножителя, т.е. скалярное произведение линейно по любому сомножителю.

3. Линейность скалярного произведения по любому сомножителю распространяется на линейные комбинации векторов:

для любых векторов [math]\mathbf_i,\,\mathbf_j[/math] и действительных чисел [math]\alpha_i,\,\beta_j,

4. Если хотя бы один сомножитель — нулевой вектор, то скалярное про изведение равно нулю:

Неравенство Коши-Буняковского

Для любых векторов [math]\mathbf[/math] и [math]\mathbf[/math] евклидова пространства [math]\mathbb[/math] выполняется неравенство Коши-Буняковского :

В самом деле, для любого действительного числа [math]\lambda[/math] и любых векторов [math]\mathbf[/math] и [math]\mathbf[/math] справедливо неравенство:

Примеры евклидовых пространств

Определяя для элементов линейного пространства операцию скалярного произведения, получаем евклидово пространство. Если скалярное произведение можно ввести разными способами в одном и том же линейном пространстве, то и получаемые евклидовы пространства будут разными. Приведем примеры евклидовых пространств, соответствующих рассмотренным ранее примерам линейных пространств.

3. В пространстве [math]\mathbb^n[/math] скалярное произведение столбцов [math]x= \beginx_1&\cdots&x_n\end^T[/math] и [math]y=\begin y_1&\cdots&y_n\end^T[/math] можно задать формулой:

Значит, выполняются аксиомы 2 и 3. Аксиома 4 также выполняется, так как квадратичная форма [math]\langle x,x\rangle= x^TAx[/math] положительно определенная. Таким образом, пространство [math]\mathbb^n[/math] со скалярным произведением (8.26) является евклидовым пространством. В частности, если в качестве матрицы [math]A[/math] взять единичную матрицу, формула (8.26) примет вид:

Приведем примеры формул, которые не задают скалярного произведения в [math]\mathbb^2:[/math]

1) [math]\langle x,y\rangle= |x_1|\cdot|y_1|+|x_2|\cdot|y_2|[/math] — аксиомы 1, 4 выполняются, а аксиомы 2, 3 — нет;

2) [math]\langle x,y\rangle=x_2\cdot y_2[/math] — аксиомы 1, 2, 3 выполняются, а аксиома 4 — нет.

4. Пространство [math]\[/math] решений однородной системы [math]Ax=o[/math] линейных уравнений со скалярным произведением (8.27) является евклидовым пространством.

6. В пространстве [math]P(\mathbb)[/math] многочленов с действительными коэффициентами скалярное произведение можно задать формулой (8.28), так как многочлены являются непрерывными функциями.

В пространстве [math]P_3(\mathbb)[/math] определим произведение формулой:

В силу симметричности и линейности правой части (8.30) по значениям многочленов, заключаем, что аксиомы 1-3 выполняются. Проверим выполнение аксиомы 4. Приравняв скалярный квадрат нулю, получаем

Длина вектора и угол между векторами в евклидовом пространстве

Углом между ненулевыми векторами [math]\mathbf[/math] и [math]\mathbf[/math] евклидова пространства [math]\mathbb[/math] называется число

Из неравенства Коши-Буняковского (8.25) следует неравенство треугольника :

Пример 8.17. Даны векторы евклидовых пространств:

y=\begin0\\1\end[/math] — элементы пространства [math]\mathbb^2[/math] со скалярным произведением (8.27): [math]\langle x,y\rangle=x_1y_1+x_2y_2[/math] ;

y=\begin0\\1\end[/math] — элементы пространства [math]\mathbb^2[/math] со скалярным произведением (8.26):

q(x)=x+2[/math] — элементы пространства [math]P_2(\mathbb)[/math] со скалярным произведением (8.29): [math]\langle p,q\rangle= a_2b_2+a_1b_1+a_0b_0[/math] ;

q(x)=x+2[/math] — элементы пространства [math]P_2(\mathbb)[/math] со скалярным произведением (8.30):

В каждом пространстве найти длины двух данных векторов и угол между ними.

Решение. а) Находим скалярные произведения:

б) Находим скалярные произведения:

в) Находим скалярные произведения:

г) Находим скалярные произведения:

\langle p,q\rangle= 1\!\cdot\!0+(-2)\!\cdot\!1+1\!\cdot\!2=0;

\langle q,q\rangle= 0\!\cdot\!0+1\!\cdot\!1+2\!\cdot\!2=5.[/math]

д) Находим скалярные произведения:

\langle p,q\rangle= 0\!\cdot\!3+1\!\cdot\!4+4\!\cdot\!5=24;

\langle q,q\rangle= 3\!\cdot\!3+4\!\cdot\!4+5\!\cdot\!5=50.[/math]

Источник

Евклидова плоскость

Евкли́дово простра́нство (также эвкли́дово пространство) в изначальном смысле — это пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность, равную 3, то есть является трёхмерным.

Содержание

Формальное определение

Длины и углы

Замечание

Алгебраические свойства

Ортонормированные базисы

Ортогональные проекции

Сопряжённые пространства и операторы

Движения евклидова пространства

Примеры

Наглядными примерами евклидовых пространств могут служить пространства:

Более абстрактный пример:

Примеры геометрических фигур в многомерном евклидовом пространстве:

Связанные определения

Под евклидовой метрикой может пониматься метрика, описанная выше, а также соответствующая риманова метрика.

Под локальной евклидовостью обычно имеют в виду то, что каждое касательное пространство риманова многообразия есть евклидово пространство со всеми вытекающими свойствами, например, возможностью (по гладкости метрики) ввести в малой окрестности точки координаты, в которых расстояние выражается (с точностью до какого-то порядка) в соответствии с описанным выше.

Метрическое пространство называют локально евклидовым также если возможно ввести на нём координаты, в которых метрика будет евклидовой (в смысле второго определения) всюду (или хотя бы на конечной области) — каковым, например, является риманово многообразие нулевой кривизны.

Вариации и обобщения

Если в качестве основного поля использовать не поле вещественных чисел, а поле комплексных, то это даст определение унитарного (или эрмитова) пространства.

Отказ от требования конечномерности даёт определение предгильбертова пространства. Отказ от требования положительной определённости скалярного произведения приводит к определению псевдоевклидова пространства. Требование того, чтобы предгильбертово пространство было полным по метрике, ведёт к определению гильбертова пространства; пространство квадратично-суммируемых последовательностей — гильбертово пространство, которое может рассматриваться как пространство векторов с бесконечным числом координат.

Источник

Евклидово пространство

Евкли́дово простра́нство (также Эвкли́дово простра́нство) — в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность 3.

В современном понимании, в более общем смысле, может обозначать один из сходных и тесно связанных объектов, определённых ниже. Обычно -мерное евклидово пространство обозначается , хотя часто используется не вполне приемлемое обозначение .

1. Конечномерное гильбертово пространство, то есть конечномерное вещественное векторное пространство с введённым на нём (положительно определенным) скалярным произведением, порождающим норму:

в простейшем случае (евклидова норма):

где (в евклидовом пространстве всегда можно выбрать базис, в котором верен именно этот простейший вариант).

2. Метрическое пространство, соответствующее пространству описанному выше. То есть с метрикой, введённой по формуле:

где и .

Содержание

Связанные определения

Примеры

Наглядными примерами евклидовых пространств могут служить пространства:

Более абстрактный пример:

Вариации и обобщения

См. также