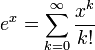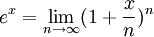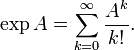Exp что это в физике

Что такое Экспонента

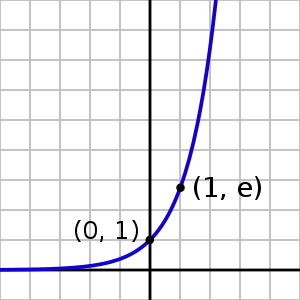
Экспонента (экспоненциальная функция) — это математическая функция вида y = e×, или у = exp(x), или у = Exp(x) (где основанием степени является число е).

е — это число Эйлера, у него бесконечное количество цифр после запятой, оно трансцендентное и иррациональное. Оно равно округлённо 2,72 (а полностью — 2,718281828459045. ).

Трансцендентным число называется, если оно не удовлетворяет ни одному алгебраическому уравнению. Иррациональным — если его нельзя представить в виде дроби m/n, где n не равно 0.

Несмотря на свою бесконечность, число е является константой. То есть значением, которое никогда не изменяется.

Показательная функция — это математическая функция вида y = a×.

График экспоненты выглядит следующим образом:

Для чего используется экспонента?

Экспонента применяется и в физике, и в технике, и в экономике, особенно при решении задач, связанных с процентами.

Экспоненциальный рост

Мы используем термин экспоненциальный рост, чтобы сказать о стремительном росте чего-либо. Словосочетание чаще всего употребляется по отношению к росту популяции людей или животных/птиц.

Что такое второй замечательный предел

Швейцарский математик Якоб Бернулли (1655–1705 гг.) вывел число е, когда пытался решить финансовый вопрос. В частности, он пытался понять, как должны начисляться проценты на сумму вклада в банке, чтобы это было наиболее прибыльно для владельца денег.

Он также пытался понять, есть ли лимит у дохода, получаемого в процентах, или он будет увеличиваться бесконечно.

Решая эту задачу, он использовал предел последовательности, а именно второй замечательный предел. Формулу для вычисления числа е можно записать следующим образом (где n — это число, стремящееся к бесконечности):

То есть числу е равняется предел, где n стремится к бесконечности, от 1, плюс 1, разделённый на n, и всё возвести в степень n.

Если подставить в данную формулу вместо n какую-нибудь очень большую цифру, можно получить очень хорошее приближение к е.
Например, подставим 1.000.000 и посчитаем на калькуляторе:

(1 + 1/1000000) ^ 1000000 = 2.7182804691

Как видите, с n = 1.000.000 мы получили достаточно хорошее приближение, с правильными 5 знаками после запятой.

Как определить число е?

Помимо второго замечательного предела, существуют и другие способы для определения числа е:

Сумма ряда

Существует мнение, что этот метод использовал сам Эйлер, когда высчитывал е.

Можно получить приближение е, рассчитав первые 7 частей этой суммы:

И эти вычисления дали нам следующий результат:

Этот метод дал нам точных 4 знака после запятой, и его достаточно легко запомнить.

Формула Муавра — Стирлинга

Также называется просто формула Стирлинга:

И в этом случае чем больше n, тем точнее будет результат.

Как запомнить число е

Можно легко запомнить 9 знаков после запятой, если заметить удивительную закономерность: после «2,7» число «1828» появляется дважды (2,7 1828 1828). В 1828 году родились Лев Толстой и Жюль Верн, а Франц Шуберт умер.

Хотите дальше? Можно и дальше! 15 знаков после запятой! Последующие цифры — это градусы углов в равнобедренном прямоугольном треугольнике ( 45°, 90°, 45°): 2,7 1828 1828 45 90 45.

Интересные факты

Экспоненциальную функцию также называют экспонента.

Показательная функция — это функция вида y=a×, где a — заданное число (основание), x — это переменная.

А если основание = е, с переменной x, то математически логарифм записывается как ln, а не как log. И его называют натуральный логарифм (логарифм с основанием е):

Логарифмическая функция, что обратная к показательной функции y = a×, a > 0, a≠1, пишется как .

Производная и первообразная экспоненциальной функции равны ей самой, т. е. (e×)’ = e×, но (a×)’ = (a×)*ln(a).

Якобу Бернулли в расчётах помогал его брат Иоганн. Один из кратеров на Луне носит их имя.

Число Непера и число Эйлера

Число Непера или Неперово число, число Эйлера — это названия для одного и того же числа е.

Шотландский математик Джон Непер придумал логарифмы. Так как число е является основанием натурального логарифма (ln x), то этому числу присвоили имя математика из Шотландии. Хотя Непер и не вычислял его.

Сам символ e был придуман в 1731 году швейцарским математиком Леонардом Эйлером. Эйлер занимался вычислениями алгоритмов и вывел его основание. А точнее основание натурального логарифма, которым и является число е.

Изобретение логарифмов в XVII веке (1614 год) шотландским математиком Джоном Непером стало одним из важнейших событий в истории математики.

Источник

Экспонента в математике – это функция «y=ex», которая отражает непрерывный рост с коэффициентом. В этой функции «е»‎ ‎– это число Эйлера, которое представляет собой постоянную (

2,72). Говоря иначе, рост любой величины прямо пропорционален ее значению.

Допустим, мы слепили снежный ком и спустили его с горы. Он начинает катиться, одновременно наращивая объем. При этом чем больше он становится, тем выше скорость его движения. И наоборот: чем быстрее он катится, тем быстрее увеличивается в размерах. Получается, что масса и скорость снежного кома (y) экспоненциально возрастают со временем (x).

Экспонента в жизни. Экспоненциальный рост

Рассмотрим примеры экспоненты и экспоненциального роста в реальной жизни.

Вклад в банке под процент. У всех процессов, идущих по экспоненте, есть одна особенность: за одно и то же количество времени их параметры меняются одинаковое количество раз.

Например, вклад в банке каждый год увеличивается на определенное количество процентов. Если положить 1000 рублей в банк под 10% годовых, то через год вклад будет составлять 1100 рублей. А в следующем году 10% будут начисляться уже исходя из суммы в 1100 рублей. То есть, вклад вырастет сильнее, и так размер прироста будет увеличиваться из года в год.

Численность животных. Чем больше популяция животных, тем больше они размножаются. Соответственно, рост численности популяции прямо пропорционален количеству особей в ней.

Чем экспоненциальный рост отличается от линейного?

Линейный рост характеризуется стабильным прибавлением постоянной, а экспоненциальный рост – это следствие многократного умножения на постоянную. То есть если линейный рост на графике представляет собой стабильную линию, то экспоненциальный рост характеризуется быстрым взлетом.

В качестве примера можно привести обычную ходьбу. Если длина одного шага составляет 1 метр, то через 6 шагов человек преодолевает расстояние в 6 метров. Это и называется линейным ростом.

При экспоненциальном росте длина каждого шага в нашем примере увеличивается в 2 раза. То есть сначала человек шагает на 1 метр, потом на 2 метра, потом на 4 метра и так далее. В таком случае за 6 шагов можно пройти 32 метра, что гораздо больше, чем в предыдущем примере.

Источник

Экспоненциальная функция

Содержание

Определение

Экспоненциальная функция может быть определена различными эквивалентными способами. Например через ряд Тейлора:

Свойства

Экспонента от комплексного аргумента

От комплексного аргумента z = x + iy экспонента определяется следующим образом:

Вариации и обобщения

Аналогично экспонента может быть определена для элемента произвольной ассоциативной алгебры. В конкретном случае требуется также доказательство того, что указанные пределы существуют.

Матричная экспонента

Экспоненту от квадратной матрицы (или линейного оператора) можно формально определить, подставив матрицу в соответствующий ряд:

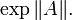
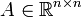
Определённый таким образом ряд сходится для любого оператора A с ограниченной нормой, поскольку мажорируется рядом для экспоненты нормы A: Следовательно, экспонента от матрицы всегда определена и сама является матрицей.

С помощью матричной экспоненты легко задать вид решения линейного дифференциального уравнения с постоянными коэффициентами: уравнение 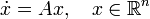с начальным условием x(0) = x₀ имеет своим решением x(t) = exp(At)x₀.

Обратная функция

Обратной функцией к экспоненциальной функции является натуральный логарифм.
Обозначается ln(x) :

См. также

Полезное

Смотреть что такое «Экспоненциальная функция» в других словарях:

ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ — то же, что показательная функция … Большой Энциклопедический словарь

экспоненциальная функция — экспонента — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия Синонимы экспонента EN exponential function … Справочник технического переводчика

экспоненциальная функция — то же, что показательная функция. * * * ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ, то же, что показательная функция (см. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ) … Энциклопедический словарь

экспоненциальная функция — eksponentinė funkcija statusas T sritis fizika atitikmenys: angl. exponential function vok. exponentielle Funktion, f rus. экспоненциальная функция, f pranc. fonction exponentielle, f … Fizikos terminų žodynas

Экспоненциальная функция — функция у = ex, то есть Показательная функция. Обозначается также y = exp х. Иногда Э. ф. называют и функцию у = ax при любом основании а > 0 … Большая советская энциклопедия

ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ — показа тельная функция, функция у=е х;обозначается также y = ехр х. Иногда Э. ф. наз. и функцию у = а х при любом основании а>0. БСЭ 3 … Математическая энциклопедия

ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ — то же, что показательная функция … Естествознание. Энциклопедический словарь

экспоненциальная — функция [ Словарь иностранных слов русского языка

Источник

Экспонента и число е: просто и понятно.

Число e всегда волновало меня — не как буква, а как математическая константа. Что число е означает на самом деле?

Разные математические книги и даже моя горячо любимая Википедия описывает эту величественную константу совершенно бестолковым научным жаргоном:

Математическая константа е является основанием натурального логарифма.

Если заинтересуетесь, что такое натуральный логарифм, найдете такое определение:

Натуральный логарифм, ранее известный как гиперболический логарифм, является логарифмом с основанием е, где е – иррациональная константа, приблизительно равная 2.718281828459.

Определения, конечно, правильные. Но понять их крайне сложно. Конечно, Википедия в этом не виновата: обычно математические пояснения сухи и формальны, составляются по всей строгости науки. Из-за этого новичкам сложно осваивать предмет (а когда-то каждый был новичком).

С меня хватит! Сегодня я делюсь своими высокоинтеллектуальными соображениями о том, что такое число е, и чем оно так круто! Отложите свои толстые, наводящие страх математические книжки в сторону!

Число е – это не просто число

Описывать е как «константу, приблизительно равную 2,71828…» — это все равно, что называть число пи «иррациональным числом, приблизительно равным 3,1415…». Несомненно, так и есть, но суть по-прежнему ускользает от нас.

Число пи — это соотношение длины окружности к диаметру, одинаковое для всех окружностей. Это фундаментальная пропорция, свойственная всем окружностям, а следовательно, она участвует в вычислении длины окружности, площади, объема и площади поверхности для кругов, сфер, цилиндров и т.д. Пи показывает, что все окружности связаны, не говоря уже о тригонометрических функциях, выводимых из окружностей (синус, косинус, тангенс).

Число е является базовым соотношением роста для всех непрерывно растущих процессов. Число е позволяет взять простой темп прироста (где разница видна только в конце года) и вычислить составляющие этого показателя, нормальный рост, при котором с каждой наносекундой (или даже быстрее) всё вырастает еще на немного.

Число е участвует как в системах с экспоненциальным, так и постоянным ростом: население, радиоактивный распад, подсчет процентов, и много-много других. Даже ступенчатые системы, которые не растут равномерно, можно аппроксимировать с помощью числа е.

Также, как любое число можно рассматривать в виде «масштабированной» версии 1 (базовой единицы), любую окружность можно рассматривать в виде «масштабированной» версии единичной окружности (с радиусом 1). И любой коэффициент роста может быть рассмотрен в виде «масштабированной» версии е («единичного» коэффициента роста).

Так что число е – это не случайное, взятое наугад число. Число е воплощает в себе идею, что все непрерывно растущие системы являются масштабированными версиями одного и того же показателя.

Понятие экспоненциального роста

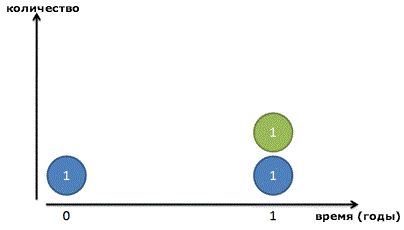
Давайте начнем с рассмотрения базовой системы, которая удваивается за определенный период времени. Например:

И выглядит это примерно так:

Деление на два или удваивание – это очень простая прогрессия. Конечно, мы можем утроить или учетверить, но удваивание более удобно для пояснения.

Математически, если у нас есть х разделений, мы получаем в 2^x раз больше добра, чем было вначале. Если сделано только 1 разбиение, получаем в 2^1 раза больше. Если разбиений 4, у нас получится 2^4=16 частей. Общая формула выглядит так:

Другими словами, удвоение – это 100% рост. Мы можем переписать эту формулу так:

Это то же равенство, мы только разделили «2» на составные части, которыми в сущности и является это число: начальное значение (1) плюс 100%. Умно, да?

Конечно, мы можем подставить и любое другое число (50%, 25%, 200%) вместо 100% и получить формулу роста для этого нового коэффициента. Общая формула для х периодов временного ряда будет иметь вид:

Это просто означает, что мы используем норму возврата, (1 + прирост), «х» раз подряд.

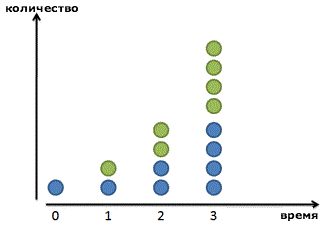
Наша формула предполагает, что прирост происходит дискретными шагами. Наши бактерии ждут, ждут, а потом бац!, и в последнюю минуту они удваиваются в количестве. Наша прибыль по процентам от депозита магическим образом появляется ровно через 1 год. На основе формулы, написанной выше, прибыль растет ступенчато. Зеленые точки появляются внезапно.

Но мир не всегда таков. Если мы увеличим картинку, мы увидим, что наши друзья-бактерии делятся постоянно:

Зеленый малый не возникает из ничего: он медленно вырастает из синего родителя. После 1 периода времени (24 часа в нашем случае), зеленый друг уже полностью созрел. Повзрослев, он стает полноценным синим членом стада и может создавать новые зеленые клеточки сам.

Эта информация как-то изменит наше уравнение?

Не-а. В случае с бактериями, полусформированные зеленые клетки все же не могут ничего делать, пока не вырастут и совсем не отделятся от своих синих родителей. Так что уравнение справедливо.

Но деньги меняют все

С деньгами дела обстоят по-другому. Как только мы зарабатываем пару монет прибыли, эти монетки начинают приносить свои микро-прибыли. Нет необходимости ждать, пока набежит целый рубль — свежим денежкам совсем не нужно дозревать, чтобы начать плодоносить.

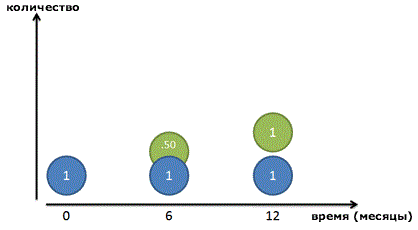
Основываясь на нашей старой формуле, прирост процента выглядит примерно так:

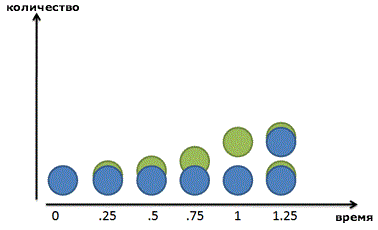
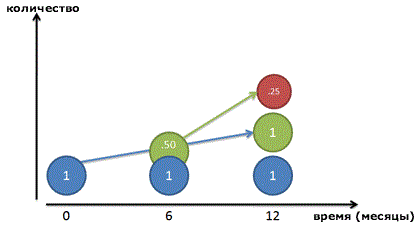
Но опять же, это не совсем правильно: вся сумма процента появляется в последний день. Давайте посмотрим поближе и разделим год на два промежутка. Мы зарабатываем 100% прибыль каждый год, или по 50% каждые 6 месяцев. Таким образом, мы заработаем 50 копеек в первые полгода, и другие 50 копеек во вторую половину года:

И все равно, это неверно! Конечно, наш рубль-родитель (Синий кружок) зарабатывает рубль в течение года. Но после 6 месяцев мы получим 50-копеечный кусочек прибыли – готовые деньги, которыми мы пренебрегаем! Эти 50 копеек уже могли бы зарабатывать свои собственные деньги:

Поскольку наш коэффициент равен 50% каждые полгода, эти 50 копеек могли бы заработать еще 25 копеек (50% от 50 копеек). В конце года мы бы получили:

Если все сложить, получится 2,25 рублей. Мы заработали 1,25 рубля всего на одном исходном рубле, и это даже лучше, чем удвоение!

Вернемся к формуле. Рост за два полу-периода по 50% составит:

Переходим на составной рост

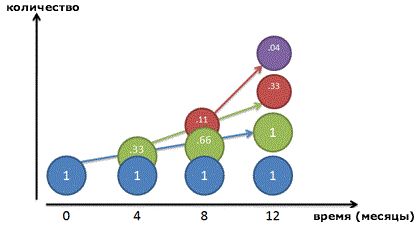
Идем дальше. Давайте поделим рост не на два периода по 50%, а на 3 сегмента по 33% каждый. Кто сказал, что надо ждать целых 6 месяцев до начала получения прибыли? Давайте детализируем наши вычисления.

Вот так выглядит наш рост, расписанный на 3 составных периода:

Фуух! Спустя 12 месяцев у нас получается: 1 + 1 + 0.33 + 0.04 или примерно 2.37 рубля.

Потратим еще чуть времени, чтобы понять, что на самом деле происходит с таким ростом:

Теперь понятнее? Поначалу это сложно — я и сам запутался, пока рисовал все эти графики. Главное понять, что каждый «рубль» создает маленьких помощников, а те, в свою очередь, создают помощников себе, и так далее.

Если рассматривать год как 3 равных периода, формула роста будет такой:

рост = (1 + 100%/3) 3 = 2.37037.

Мы заработали 1.37 рубля, а это даже лучше, чем те 1.25, что получились у нас в предыдущий раз!

Можно ли преумножать деньги бесконечно?

А почему бы не разбить год на более короткие периоды? Как насчет месяца, дня, часа или даже наносекунды? Наша прибыль взлетит до небес?

Прибыль увеличится, но уже не намного. Попробуем подставить в нашу волшебную формулу разные значения n, и получим следующее:

Источник

Exp что это в физике

Смотреть что такое «exp» в других словарях:

Exp — EXP, Exp, exp, or ExP can mean:* Exponential function in mathematics, written exp(x) or ex. * Expiration date of organic compounds like food or medicines. * Experience points in role playing games. * EXPTIME, a complexity class in computing. *… … Wikipedia

EXP — oder EXP ist die Abkürzung für: Exponentialfunktion, eine mathematische Funktion Erfahrungspunkte (engl. experience points) in Rollenspielen EXPTIME, eine Komplexitätsklasse der Komplexitätstheorie Exponentialverteilung, eine stetige… … Deutsch Wikipedia

Exp — oder EXP ist die Abkürzung für: Exponentialfunktion, eine mathematische Funktion Exponentialverteilung, eine stetige Wahrscheinlichkeitsverteilung Erfahrungspunkte (englisch experience points) in Rollenspielen EXPTIME, eine… … Deutsch Wikipedia

exp — abbrev. 1. expenses 2. experience 3. experiment 4. expiration 5. expires 6. export 7. express * * * exp abbr … Universalium

exp. — exp. exp. abbrexpense, export, express Merriam Webster’s Dictionary of Law. Merriam Webster. 1996 … Law dictionary

exp — exp, Funktionszeichen für die e Funktion (Exponentialfunktion) … Universal-Lexikon

EXP — sigla espresso … Dizionario italiano

exp — abbrev. 1. expenses 2. experience 3. experiment 4. expiration 5. expires 6. export 7. express … English World dictionary

exp. — 1. expenses. 2. expired. 3. exponential. 4. export. 5. exported. 6. exporter. 7. express. * * * abbrev 1. Experiment or experimental 2. Expired 3. Expiry … Useful english dictionary

Exp — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Exp est en mathématique l abréviation de fonction exponentielle ; Exp est un groupe de dance. exp est une firme qui fournit des services conseils… … Wikipédia en Français

Источник