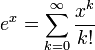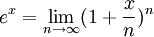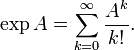Exp в формуле что означает

Экспонента в математике – это функция «y=ex», которая отражает непрерывный рост с коэффициентом. В этой функции «е»‎ ‎– это число Эйлера, которое представляет собой постоянную (

2,72). Говоря иначе, рост любой величины прямо пропорционален ее значению.

Допустим, мы слепили снежный ком и спустили его с горы. Он начинает катиться, одновременно наращивая объем. При этом чем больше он становится, тем выше скорость его движения. И наоборот: чем быстрее он катится, тем быстрее увеличивается в размерах. Получается, что масса и скорость снежного кома (y) экспоненциально возрастают со временем (x).

Экспонента в жизни. Экспоненциальный рост

Рассмотрим примеры экспоненты и экспоненциального роста в реальной жизни.

Вклад в банке под процент. У всех процессов, идущих по экспоненте, есть одна особенность: за одно и то же количество времени их параметры меняются одинаковое количество раз.

Например, вклад в банке каждый год увеличивается на определенное количество процентов. Если положить 1000 рублей в банк под 10% годовых, то через год вклад будет составлять 1100 рублей. А в следующем году 10% будут начисляться уже исходя из суммы в 1100 рублей. То есть, вклад вырастет сильнее, и так размер прироста будет увеличиваться из года в год.

Численность животных. Чем больше популяция животных, тем больше они размножаются. Соответственно, рост численности популяции прямо пропорционален количеству особей в ней.

Чем экспоненциальный рост отличается от линейного?

Линейный рост характеризуется стабильным прибавлением постоянной, а экспоненциальный рост – это следствие многократного умножения на постоянную. То есть если линейный рост на графике представляет собой стабильную линию, то экспоненциальный рост характеризуется быстрым взлетом.

В качестве примера можно привести обычную ходьбу. Если длина одного шага составляет 1 метр, то через 6 шагов человек преодолевает расстояние в 6 метров. Это и называется линейным ростом.

При экспоненциальном росте длина каждого шага в нашем примере увеличивается в 2 раза. То есть сначала человек шагает на 1 метр, потом на 2 метра, потом на 4 метра и так далее. В таком случае за 6 шагов можно пройти 32 метра, что гораздо больше, чем в предыдущем примере.

Источник

Что такое Экспонента

Экспонента (экспоненциальная функция) — это математическая функция вида y = e×, или у = exp(x), или у = Exp(x) (где основанием степени является число е).

е — это число Эйлера, у него бесконечное количество цифр после запятой, оно трансцендентное и иррациональное. Оно равно округлённо 2,72 (а полностью — 2,718281828459045. ).

Трансцендентным число называется, если оно не удовлетворяет ни одному алгебраическому уравнению. Иррациональным — если его нельзя представить в виде дроби m/n, где n не равно 0.

Несмотря на свою бесконечность, число е является константой. То есть значением, которое никогда не изменяется.

Показательная функция — это математическая функция вида y = a×.

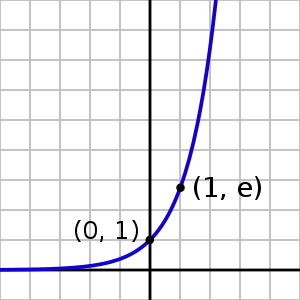
График экспоненты выглядит следующим образом:

Для чего используется экспонента?

Экспонента применяется и в физике, и в технике, и в экономике, особенно при решении задач, связанных с процентами.

Экспоненциальный рост

Мы используем термин экспоненциальный рост, чтобы сказать о стремительном росте чего-либо. Словосочетание чаще всего употребляется по отношению к росту популяции людей или животных/птиц.

Что такое второй замечательный предел

Швейцарский математик Якоб Бернулли (1655–1705 гг.) вывел число е, когда пытался решить финансовый вопрос. В частности, он пытался понять, как должны начисляться проценты на сумму вклада в банке, чтобы это было наиболее прибыльно для владельца денег.

Он также пытался понять, есть ли лимит у дохода, получаемого в процентах, или он будет увеличиваться бесконечно.

Решая эту задачу, он использовал предел последовательности, а именно второй замечательный предел. Формулу для вычисления числа е можно записать следующим образом (где n — это число, стремящееся к бесконечности):

То есть числу е равняется предел, где n стремится к бесконечности, от 1, плюс 1, разделённый на n, и всё возвести в степень n.

Если подставить в данную формулу вместо n какую-нибудь очень большую цифру, можно получить очень хорошее приближение к е.
Например, подставим 1.000.000 и посчитаем на калькуляторе:

(1 + 1/1000000) ^ 1000000 = 2.7182804691

Как видите, с n = 1.000.000 мы получили достаточно хорошее приближение, с правильными 5 знаками после запятой.

Как определить число е?

Помимо второго замечательного предела, существуют и другие способы для определения числа е:

Сумма ряда

Существует мнение, что этот метод использовал сам Эйлер, когда высчитывал е.

Можно получить приближение е, рассчитав первые 7 частей этой суммы:

И эти вычисления дали нам следующий результат:

Этот метод дал нам точных 4 знака после запятой, и его достаточно легко запомнить.

Формула Муавра — Стирлинга

Также называется просто формула Стирлинга:

И в этом случае чем больше n, тем точнее будет результат.

Как запомнить число е

Можно легко запомнить 9 знаков после запятой, если заметить удивительную закономерность: после «2,7» число «1828» появляется дважды (2,7 1828 1828). В 1828 году родились Лев Толстой и Жюль Верн, а Франц Шуберт умер.

Хотите дальше? Можно и дальше! 15 знаков после запятой! Последующие цифры — это градусы углов в равнобедренном прямоугольном треугольнике ( 45°, 90°, 45°): 2,7 1828 1828 45 90 45.

Интересные факты

Экспоненциальную функцию также называют экспонента.

Показательная функция — это функция вида y=a×, где a — заданное число (основание), x — это переменная.

А если основание = е, с переменной x, то математически логарифм записывается как ln, а не как log. И его называют натуральный логарифм (логарифм с основанием е):

Логарифмическая функция, что обратная к показательной функции y = a×, a > 0, a≠1, пишется как .

Производная и первообразная экспоненциальной функции равны ей самой, т. е. (e×)’ = e×, но (a×)’ = (a×)*ln(a).

Якобу Бернулли в расчётах помогал его брат Иоганн. Один из кратеров на Луне носит их имя.

Число Непера и число Эйлера

Число Непера или Неперово число, число Эйлера — это названия для одного и того же числа е.

Шотландский математик Джон Непер придумал логарифмы. Так как число е является основанием натурального логарифма (ln x), то этому числу присвоили имя математика из Шотландии. Хотя Непер и не вычислял его.

Сам символ e был придуман в 1731 году швейцарским математиком Леонардом Эйлером. Эйлер занимался вычислениями алгоритмов и вывел его основание. А точнее основание натурального логарифма, которым и является число е.

Изобретение логарифмов в XVII веке (1614 год) шотландским математиком Джоном Непером стало одним из важнейших событий в истории математики.

Источник

Для действительных чисел c и d функция формы также является экспоненциальной функцией, поскольку ее можно переписать как ж ( Икс ) знак равно а б c Икс + d <\ Displaystyle е (х) = ab ^ >

Экспоненциальную функцию иногда называют естественной экспоненциальной функцией, чтобы отличить ее от других экспоненциальных функций. Изучение любой экспоненциальной функции легко сводится к изучению естественной экспоненциальной функции, поскольку ж ( Икс ) знак равно е Икс <\ Displaystyle е (х) = е ^ <х>>

Как функции действительной переменной экспоненциальные функции однозначно характеризуются тем фактом, что скорость роста такой функции (то есть ее производной ) прямо пропорциональна значению функции. Константа пропорциональности этого отношения является натуральным логарифмом основания b :

Показательная функция удовлетворяет фундаментальному мультипликативному тождеству (которое также может быть расширено на комплексные показатели):

Аргументом экспоненциальной функции может быть любое действительное или комплексное число или даже математический объект совершенно другого типа (например, квадратная матрица ).

СОДЕРЖАНИЕ

Формальное определение

Посредством биномиальной теоремы и определения степенного ряда экспоненциальная функция также может быть определена как следующий предел:

Обзор

Производные и дифференциальные уравнения

Кроме того, для любой дифференцируемой функции f ( x ) по цепному правилу находим :

Непрерывные дроби для e x

или, применив замену z = Икс / у :

со специальным случаем для z = 2 :

Сложная плоскость

Как и в реальном случае, экспоненциальная функция может быть определена на комплексной плоскости в нескольких эквивалентных формах. Наиболее распространенное определение комплексной экспоненциальной функции аналогично определению степенного ряда для вещественных аргументов, где действительная переменная заменяется комплексной:

В качестве альтернативы, комплексная экспоненциальная функция может быть определена путем моделирования определения предела для реальных аргументов, но с заменой реальной переменной на сложную:

Определение комплексной экспоненциальной функции, в свою очередь, приводит к соответствующим определениям, расширяющим тригонометрические функции до сложных аргументов.

В частности, когда z = it ( t real), определение ряда дает разложение

В этом разложении преобразование членов в действительную и мнимую части оправдано абсолютной сходимостью ряда. Действительная и мнимая части приведенного выше выражения фактически соответствуют разложениям в ряды cos t и sin t соответственно.

Эти определения экспоненциальной и тригонометрической функций тривиально приводят к формуле Эйлера :

exp ⁡ ( я z ) знак равно потому что ⁡ z + я грех ⁡ z для всех z ∈ C <\ Displaystyle \ ехр (iz) = \ соз z + я \ грех Z <\ текст <для всех>> z \ in \ mathbb > .

Когда ее область определения расширяется от вещественной линии до комплексной плоскости, экспоненциальная функция сохраняет следующие свойства:

Затем мы можем определить более общее возведение в степень:

См. Отказ от тождества мощности и логарифма для получения дополнительной информации о проблемах с объединением степеней.

Источник

Экспоненциальная функция

Содержание

Определение

Экспоненциальная функция может быть определена различными эквивалентными способами. Например через ряд Тейлора:

Свойства

Экспонента от комплексного аргумента

От комплексного аргумента z = x + iy экспонента определяется следующим образом:

Вариации и обобщения

Аналогично экспонента может быть определена для элемента произвольной ассоциативной алгебры. В конкретном случае требуется также доказательство того, что указанные пределы существуют.

Матричная экспонента

Экспоненту от квадратной матрицы (или линейного оператора) можно формально определить, подставив матрицу в соответствующий ряд:

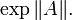
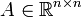
Определённый таким образом ряд сходится для любого оператора A с ограниченной нормой, поскольку мажорируется рядом для экспоненты нормы A: Следовательно, экспонента от матрицы всегда определена и сама является матрицей.

С помощью матричной экспоненты легко задать вид решения линейного дифференциального уравнения с постоянными коэффициентами: уравнение 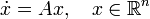с начальным условием x(0) = x₀ имеет своим решением x(t) = exp(At)x₀.

Обратная функция

Обратной функцией к экспоненциальной функции является натуральный логарифм.
Обозначается ln(x) :

См. также

Полезное

Смотреть что такое «Экспоненциальная функция» в других словарях:

ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ — то же, что показательная функция … Большой Энциклопедический словарь

экспоненциальная функция — экспонента — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия Синонимы экспонента EN exponential function … Справочник технического переводчика

экспоненциальная функция — то же, что показательная функция. * * * ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ, то же, что показательная функция (см. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ) … Энциклопедический словарь

экспоненциальная функция — eksponentinė funkcija statusas T sritis fizika atitikmenys: angl. exponential function vok. exponentielle Funktion, f rus. экспоненциальная функция, f pranc. fonction exponentielle, f … Fizikos terminų žodynas

Экспоненциальная функция — функция у = ex, то есть Показательная функция. Обозначается также y = exp х. Иногда Э. ф. называют и функцию у = ax при любом основании а > 0 … Большая советская энциклопедия

ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ — показа тельная функция, функция у=е х;обозначается также y = ехр х. Иногда Э. ф. наз. и функцию у = а х при любом основании а>0. БСЭ 3 … Математическая энциклопедия

ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ — то же, что показательная функция … Естествознание. Энциклопедический словарь

экспоненциальная — функция [ Словарь иностранных слов русского языка

Источник

Формула Эйлера и приближенные методы

Илья Бирман в заметке о числах π и e написал об их связи со мнимой единицей:

Числа π и e входят в мою любимую формулу — формулу Эйлера, которая связывает 5 самых главных констант — ноль, единицу, мнимую единицу i и, собственно, числа π и е:

Почему число 2,7182818284590 в комплексной степени 3,1415926535i вдруг равно минус единице? Ответ на этот вопрос выходит за рамки заметки и мог бы составить содержание небольшой книги, которая потребует некоторого начального понимания тригонометрии, пределов и рядов.

Экспоненциальная функция

$$\begin[scale=1.0544]\small \begin[axis line style=gray, samples=120, width=11.3cm,height=7.158cm, xmin=-2.1, xmax=2.1, ymin=0, ymax=1.8, restrict y to domain=-0.2:2, ytick=<1>, xtick=<-1,1>, axis equal, axis x line=center, axis y line=center, xlabel=$x$,ylabel=$y$] \addplot[red,domain=-2:1,semithick]; \addplot[black]; \addplot[] coordinates <(1,1.5)>node<$y=x+1$>; \addplot[red] coordinates <(-1,0.6)>node<$y=e^x$>; \path (axis cs:0,0) node [anchor=north west,yshift=-0.07cm] <0>; \end \end$$

Чем больше n, тем меньше аргумент экспоненты x/n и тем точнее работает эта формула.

Комплексные числа

$$\begin[semithick,scale=1.0545]\small \tikzset<>=stealth> \def\r <2.3>\def\l <4>\def\ll <\l*0.8>\def\h <0.6>\def\a <2.4>\def\b <1.8>\def\t <0.07>\def\p <0.5>\draw[->,thin,gray](-\h,0)—(\l,0); \draw[->,thin,gray](0,-\h)—(0,\ll); \draw[red!50!black](0,0)—(\a,0) node[midway,below] <$a$>; \draw[black!50!green](\a,0)—(\a,\b) node[midway,right] <$b$>; \draw[->,black!40!blue](0,0)—(\a,\b) node[midway,above] <$r$>node[p=1,above,black] <$(a,b)$>; \draw[thin](\p,0) arc (0:atan2(\b,\a):\p) node[midway,right,yshift=0.06cm] <$\alpha$>; \path(0,0) node [anchor=north west,yshift=-0.07cm] <0>; \draw[line width=0.21mm,opacity=0] (-\h,-\h) rectangle (\l,\ll); \end$$

Представление в виде вектора удобно, когда речь идет о сумме комплексных чисел. Тогда вектор, соответствующий сумме комплексных чисел, равен сумме векторов, соответствующих каждому слагаемому. К сожалению, у произведения комплексных чисел нет такой наглядной картины. Тем не менее, чтобы сформулировать относительно простое правило для представления произведения в виде вектора, перейдем от декартовых координат к полярным координатам r и α. Первое число задает длину вектора и называется модулем комплексного числа, а второе есть угол между вектором и осью абсцисс и называется аргументом. Ясно, что каждая пара этих чисел, r и α, тоже однозначно задает свой вектор и свое комплексное число.

Теперь можно сформулировать правило умножения в терминах длины вектора и его направления (оно выведено в дополнении к заметке). Длина вектора произведения равна произведению длин векторов сомножителей, а аргумент (угол между вектором и осью абсцисс) равен сумме аргументов. Я изобразил это правило на рисунке. Здесь синий вектор равен произведению зеленого и красного.

Возведение в комплексную степень

Чтобы всё же определить возведение в комплексную степень, нужно привлечь дополнительные принципы или соображения по отношению к правилам арифметики. В качестве такого принципа я предлагаю считать разложение e x ≈ 1 + x около нуля справедливым не только для действительных x, но и для комплексных.

(1 + iπ/10) 1 = 1 + 0,3142i
(1 + iπ/10) 2 = 1 + 2·0,3142i − 0,3142 2 = 0,9013 + 0,6283i
(1 + iπ/10) 3 = 0,7039 + 0,9115i
(1 + iπ/10) 4 = 0,4176 + 1,1326i
(1 + iπ/10) 5 = 0,0617 + 1,2638i
(1 + iπ/10) 6 = −0,3352 + 1,2832i
(1 + iπ/10) 7 = −0,7384 + 1,1779i
(1 + iπ/10) 8 = −1,1085 + 0,9459i
(1 + iπ/10) 9 = −1,4056 + 0,5976i
(1 + iπ/10) 10 = −1,5934 + 0,1561i

Вот эти числа на рисунке:

В соответствии с правилом умножения, аргумент растет как арифметическая прогрессия, а модуль — как геометрическая. К сожалению, из-за небольшого n наша формула слишком неточная, и мы пришли к числу вместо ожидаемого −1. Но зато мы понимаем процедуру, которая при неограниченном росте n даст нужное значение.

Действительно, чем меньше число iπ/n, тем с большей точностью отрезок касательной iπ/n приближает дугу окружности, тем ближе к π/n угол между соседними векторами и тем меньше отклонение длины векторов от 1. В пределе мы получим точки окружности единичного радиуса, а само число попадет в −1. Прямые вычисления это подтверждают:

(1 + iπ/100) 100 = −1,0506 + 0,001085i,
(1 + iπ/1000) 1000 = −1,004946 + 0,00001039i,
(1 + iπ/10000) 10000 = −1,0004936 + 1,03·10 −7 i.

Дополнение 1. Привлечение математической строгости

Я на простых примерах рассказал о том, как ведут себя числа и функции. Математики обычно не используют изложенный выше способ рассуждений, хотя его можно сделать вполне строгим с помощью понятий предела и «о малого».

В более продвинутом курсе теории функций комплексной переменной вводится понятие аналитической функции. Это такая функция f, которая раскладывается в ряд Тейлора, который сходится к самой функции f. (Для того чтобы комплексная функция была аналитической в какой-то области, достаточно, чтобы она была дифференцируемой в этой области. Требование дифференцируемости в комплексном случае гораздо сильнее, чем в действительном. Комплексная дифференцируемая функция в области бесконечно дифференцируема и аналитична на ней.) Оказывается, что аналитическую функцию, определенную для действительных чисел, можно единственным образом продолжить в область комплексных чисел, чтобы функция осталась аналитической. В этом и состоит обоснование выбора определения комплексной экспоненты через ряды: мы специально выбираем экспоненту в виде ряда, чтобы получилась аналитическая функция.

Дополнение 2. Тригонометрическая форма и умножение комплексных чисел

$$\begin[semithick,scale=1.0545]\small \tikzset<>=stealth> \def\r <2.3>\def\l <4>\def\ll <\l*0.8>\def\h <0.6>\def\a <2.4>\def\b <1.8>\def\t <0.07>\def\p <0.5>\draw[->,thin,gray](-\h,0)—(\l,0); \draw[->,thin,gray](0,-\h)—(0,\ll); \draw[red!50!black](0,0)—(\a,0) node[midway,below] <$a$>; \draw[black!50!green](\a,0)—(\a,\b) node[midway,right] <$b$>; \draw[->,black!40!blue](0,0)—(\a,\b) node[midway,above] <$r$>node[p=1,above,black] <$(a,b)$>; \draw[thin](\p,0) arc (0:atan2(\b,\a):\p) node[midway,right,yshift=0.06cm] <$\alpha$>; \path(0,0) node [anchor=north west,yshift=-0.07cm] <0>; \draw[line width=0.21mm,opacity=0] (-\h,-\h) rectangle (\l,\ll); \end$$

Перемножим два комплексных числа в тригонометрической форме:

Вспоминая тригонометрические формулы, видим, что в круглых скобках получились выражения для косинуса и синуса суммы углов. Окончательный ответ имеет вид

Таким образом, модуль произведения комплексных чисел равен произведению модулей сомножителей, а аргумент произведения есть сумма произведений сомножителей.

Дополнение 3. О приближенных методах вычислений

В физике постоянно используются приближенные методы, особенно разложение в ряд Тейлора до первого (изредка до второго) слагаемого. Дело в том, что аналитическое решение в виде формулы можно получить разве что в простейших задачах. Численно, на компьютере, тоже не всякая задача решается. Поэтому часто в ходе преобразований приходится что-нибудь раскладывать и чем-нибудь пренебрегать.

Иногда приближенные методы удается использовать и в арифметических задачах. Прекрасный пример встречается в книге «Вы, конечно, шутите, мистер Фейнман»:

Тут в ресторан вошел японец. Я уже раньше видел его: он бродил по городу, пытаясь продать счеты. Он начал разговаривать с официантами и бросил им вызов, заявив, что может складывать числа быстрее, чем любой из них.

Официанты не хотели потерять лицо, поэтому сказали: «Да, да, конечно. А почему бы Вам не пойти к тому посетителю и не устроить соревнование с ним?»

Этот человек подошел ко мне. Я попытался сопротивляться: «Я плохо говорю на португальском!»

Официанты засмеялись. «С числами это не имеет значения», — сказали они.

Они принесли мне карандаш и бумагу.

Человек попросил официанта назвать несколько чисел, которые нужно сложить. Он разбил меня наголову, потому что пока я писал числа, он уже складывал их.

Тогда я предложил, чтобы официант написал два одинаковых списка чисел и отдал их нам одновременно. Разница оказалась небольшой. Он опять выиграл у меня приличное время.

Однако японец вошел в раж: он хотел показать, какой он умный. «Multiplicao!» — сказал он.

Кто-то написал задачу. Он снова выиграл у меня, хотя и не так много, потому что я довольно прилично умею умножать.

А потом этот человек сделал ошибку: он предложил деление. Он не понимал одного: чем сложнее задача, тем у меня больше шансов победить.

Нам дали длинную задачу на деление. Ничья.

Это весьма обеспокоило японца, потому что он явно прекрасно умел выполнять арифметические операции с помощью счет, а тут его почти победил какой-то посетитель ресторана.

«Raios cubicos!» — мстительно говорит он. Кубические корни! Он хочет брать кубические корни с помощью арифметики! Трудно найти более сложную фундаментальную задачу в арифметике. Должно быть, это был его конек в упражнениях со счетами.

Он пишет на бумаге число — любое большое число — я до сих пор его помню: 1729,03. Он начинает работать с этим числом и при этом что-то бормочет и ворчит: «Бу-бу-бу-хм-гм-бу-бу», — он трудится как демон! Он просто погружается в этот кубический корень!

Я же тем временем просто сижу на своем месте.

Один из официантов говорит: «Что Вы делаете?»

Я указываю на голову. «Думаю!» — говорю я. Затем пишу на бумаге 12. Еще через какое-то время — 12,002.

Человек со счетами вытирает со лба пот и говорит: «Двенадцать!»

«О, нет! — возражаю я. — Больше цифр! Больше цифр!» Я знаю, что, когда с помощью арифметики берешь кубический корень, то каждая последующая цифра требует большего труда, чем предыдущая. Это работа не из легких.

Он опять уходит в работу и при этом бормочет: «Уф-фыр-хм-уф-хм-гм. ». Я же добавляю еще две цифры. Наконец, он поднимает голову и говорит: «12,0!»

Официанты просто светятся от счастья. Они говорят японцу: «Смотрите! Он делает это в уме, а Вам нужны счеты! И цифр у него больше!»

Он был абсолютно измотан и ушел, побежденный и униженный. Официанты поздравили друг друга.

Каким же образом посетитель выиграл у счетов? Число было 1729,03. Я случайно знал, что в кубическом футе 1728 кубических дюймов, так что было ясно, что ответ немногим больше 12. Излишек же, равный 1,03, — это всего лишь одна часть из почти 2000, а во время курса исчисления я запомнил, что для маленьких дробей излишек кубического корня равен одной трети излишка числа. Так что мне пришлось лишь найти дробь 1/1728, затем умножить полученный результат на 4 (разделить на 3 и умножить на 12). Вот так мне удалось получить целую кучу цифр.

Несколько недель спустя этот человек вошел в бар того отеля, в котором я остановился. Он узнал меня и подошел. «Скажите мне, — спросил он, — как Вам удалось так быстро решить задачу с кубическим корнем?»

Я начал объяснять, что использовал приближенный метод, и мне достаточно было определить процент ошибки. «Допустим, Вы дали мне число 28. Кубический корень из 27 равен 3. »

Он берет счеты: жжжжжжжжжжжжжжжж — «Да», — соглашается он.

И тут до меня доходит: он не знает чисел. Когда у тебя есть счеты, не нужно запоминать множество арифметических комбинаций; нужно просто научится щелкать костяшками вверх-вниз. Нет необходимости запоминать, что 9 + 7 = 16; ты просто знаешь, что когда прибавляешь 9, то нужно передвинуть десятичную костяшку вверх, а единичную — вниз. Поэтому основные арифметические действия мы выполняем медленнее, зато мы знаем числа.

Более того, сама идея о приближенном методе вычисления была за пределами его понимания, несмотря на то, что зачастую невозможно найти метод точного вычисления кубического корня. Поэтому мне так и не удалось научить его брать кубический корень или объяснить, как мне повезло, что он выбрал число 1729,03.

В этом приближенном ответе благодаря малости числа 1,03/1728 по сравнению с единицей все цифры точные, расхождение с правильным ответом начинается в шестом знаке после запятой. Самая сложная операция в приведенной цепочке — вычисление дроби 1,03/432.

Источник