Fplot matlab что это

Иллюстрированный самоучитель по MatLab

Графическая функция fplot

Разумеется, MATLAB имеет средства для построения графиков и таких функций, как sin(x)/x, которые имеют устранимые неопределенности. Не обсуждая эти средства подробно, просто покажем, как это делается, с помощью другой графической команды:

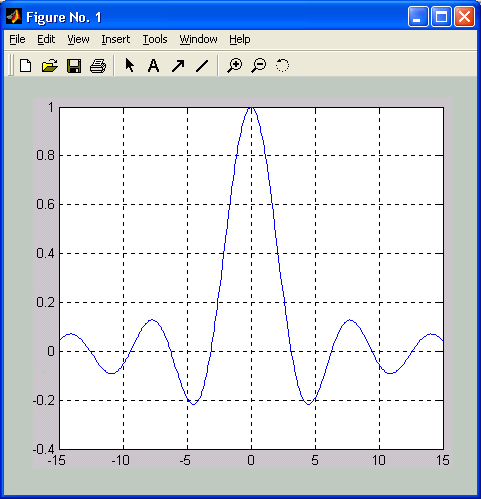
Она позволяет строить функцию, заданную в символьном виде, в интервале изменения аргумента х от xmin до xmax без фиксированного шага изменения х. Один из вариантов ее применения демонстрирует рис. 3.3. Хотя в процессе вычислений предупреждение об ошибке (деление на 0) выводится, но график строится правильно, при х=0 sinx/x=1. Обратите также внимание на две используемые команды: clear (очистить) – очистка графического окна и grid on (сетка) – включение отображения сетки, которая строится пунктирными линиями.

Рис. 3.3. Построение графика sin(x)/x функцией fplot

На рис. 3.3 представлено также меню File (Файл) окна графики. Нетрудно заметить, что оно содержит типовые файловые операции. Однако они относятся не к файлам документов, а к файлам графиков. В частности, можно присваивать имя записываемым на диск рисункам с графиками.

Позже мы более подробно рассмотрим возможности различных графических команд. В частности, покажем, как можно задавать определенный цвет и стиль линий, как менять вывод координатных осей, наносить на графики различные текстовые надписи и выполнять множество иных операций форматирования графиков для придания им более наглядного вида, соответствующего требованиям пользователя. Мы также обсудим множество новых форм применения графических команд, резко расширяющих их возможности построения графиков всех мыслимых типов.

Источник

5. Графическая функция fplot

Графическая функция fplot

Разумеется, MATLAB имеет средства для построения графиков и таких функций, как sin(x)/x, которые имеют устранимые неопределенности. Не обсуждая эти средства подробно, просто покажем, как это делается, с помощью другой графической команды —

fplot: fplott’f(x)’. [xmin xmax])

Она позволяет строить функцию, заданную в символьном виде, в интервале изменения аргумента х от xmin до xmax без фиксированного шага изменения х. Один из вариантов ее применения демонстрирует рис. 3.3. Хотя в процессе вычислений предупреждение об ошибке (деление на 0) выводится, но график строится правильно, при х=0 sinx/x=l. Обратите также внимание на две используемые команды: clear (очистить)— очистка графического окна и grid on (сетка)— включение отображения сетки, которая строится пунктирными линиями.

Рис. 3.3. Построение графика sin(x)/x функцией fplot

На рис. 3.3 представлено также меню File (Файл) окна графики. Нетрудно заметить, что оно содержит типовые файловые операции. Однако они относятся не к файлам документов, а к файлам графиков. В частности, можно присваивать имя записываемым на диск рисункам с графиками.

Позже мы более подробно рассмотрим возможности различных графических команд. В частности, покажем, как можно задавать определенный цвет и стиль линий, как менять вывод координатных осей, наносить на графики различные текстовые надписи и выполнять множество иных операций форматирования графиков для придания им более наглядного вида, соответствующего требованиям пользователя. Мы также обсудим множество новых форм применения графических команд, резко расширяющих их возможности построения графиков всех мыслимых типов.

Источник

2. Графика matlab

График даёт самую полную общую информацию о функции, поэтому в системах компьютерной математики большое внимание уделяется средствам построения графиков функций.

Функция plot() строит графики кривых с массивами значений абсцисс и ординат и имеет следующий формат:

Строка s используется для задания параметров графика: типа, толщины и цвета рисуемой линии, а также формы и размера меток на графике. Строка s может отсутствовать, тогда MATLAB устанавливает параметры, действующие по умолчанию: все кривые выводятся сплошными линиями, окрашенными циклически в шесть различных цветов.

Переменная s представляет собой строку символов, и эту строку можно подготовить в отдельной команде или записать непосредственно в команде построения графика, например

Таблица кодировки типов линий при выводе графика функции

Таблица кодировки цвета линии графика функции

Таблица кодировки меток на графике

^ v > > x=0:0.01:3; y=exp(x).*sin(9*x); plot(x, y,’r-‘)

Для построения графиков используется специальный графический редактор, который строит на экране графическое окно и в нём рисует график. Вызывается графический редактор автоматически при выполнении графических функций. По умолчанию производится разметка осей координат и иногда выводится заголовок сверху графика. Графический редактор имеет свои средства модификации графика и нанесения на график различных надписей и символов. Например, заголовок создаёт функция titke(‘text’), причём в качестве параметра text можно использовать и формулу.

Пример. Построить график функции с заголовком.

Текст можно вывести в заданное координатами место графика функцией .

>> text(0.5, 15, ‘grafik y=exp(x)sin(9x)’)

Координаты вывода текста можно указать на графике мышью, если использовать функцию . Тогда после вывода графика и выполнения команды

нужно указать мышью место на графике и щёлкнуть.

На одном чертеже можно построить графики нескольких функций, для этого нужно попарно перечислить векторы, задающие абсциссы и ординаты. Для идентификации графиков можно использовать команду legend(), позволяющую связать с каждой кривой некоторую текстовую информацию.

Пример. Построить на одном чертеже графики функций и

>> x=0:0.02:pi; y=exp(x);z=sin(9*x);plot(x, y,x, z), legend(‘exp(x)’, ‘sin(9x)’)

Имеется другой способ размещения на одном чертеже графиков нескольких функций: сформировать матрицу, столбцы которой должны содержать нужные ординаты. Ординаты обычно удобно задавать строками, тогда для построения графиков строки необходимо транспонировать.

Пример. Построить на одном чертеже графики функций .

а) Построить график функции на промежутке с шагом . График рисовать сплошной линией красного цвета.

6) Построить график функции на промежутке с шагом . График рисовать пунктирной линией чёрного цвета с маркерами в виде пятиконечной звезды размера 5.

в) Построить на одном чертеже графики функций .

г) Построить на одном чертеже графики функций . Использовать функцию для идентификации графиков.

д) Построить на одном чертеже графики функций . Использовать функцию .

Функция ezplot() применяется для рисования графиков неявно заданных функции двух переменных и параметрически заданных функций. Эта функция рисует также графики функций одной переменной, причём, в огтличие от функции plot(), шаг и нужные массивы значений абсцисс и ординат соэдаются автоматически. Функция ezplot() автоматически выводит над графиками наименование функций.

Пример. Построить на промежутке график функции . Нанести на график сетку.

Пример. Построить на промежутке график неявной функции, заданной уравнением .

Функция ezplot() особенно удобна для определения начального приближения решения системы двух уравнений графическом методом Нужно построить на одном чертеже графики двух неявных функций и . Эту задачу решают две последовательно выполненные команды

В первой команде используется функция hold, чтобы сохранить рисунок для последующего наложения на него второго рисунка.

Пример. Найти начальное приближение решения системы

Рисунок показывает, что система имеет четыре решения, приближённые значения которых есть , , , .

2.3. Построение нескольких рисунков в одном графическом окне

В одном графическом окне можно разместить несколько рисунков, используя функцию subplot(N,M,K). Эта функция создаёт массив графиков, состоящий из N рисунков по вертикали и M рисунков по горизонтали. В результате выполнения функции subplot(N,M,K) активным становится рисунок с номером K. Нумерация ведётся слева направо и сверху вниз. Крайний слева рисунок из верхнего ряда считается первым, а крайний справа из нижнего ряда имеет номер N*M.

Пример. В одном графическом окне построить графики четырёх функций: на промежутке , на промежутке , на промежутке и на промежутке .

Решение. Выполним следующие команды, не закрывая графического окна:

>> subplot(2,2,1), ezplot(‘x^2’,[-5,5]), xlabel(»),grid

>> subplot(2,2,2), ezplot(‘exp(x)’,[-2,2]), xlabel(»),grid

>> subplot(2,2,3), ezplot(‘log(x)’,[0,5]), xlabel(»),grid

>> subplot(2,2,4), ezplot(‘sqrt(x)’,[0,10]), xlabel(»),grid

В командах вывода графиков использована функция xlabel(‘’) с аргументом в виде пустой строки, которая отменяет вывод обозначения горизонтальной оси. Если этого не сделать, то символ обозначения оси наложится на наименование функций нижних графиков.

Функция fplot(‘f(x)’, [xmin, xmax]), аналогично функции plot(), строит график функции f(x), однако при использовании функции fplot() не требуется задавать массив значений аргумента и вычислять массив

значений функции, всё это делается автоматически. График строится на промежутке изменения аргумента x от xmin до xmax.

Пример. Построить график функции на промежутке .

Решение. Используем функцию fplot():

2.5. Трёхмерная графика

Чтобы построить поверхность , нужно иметь массив значений функции , вычисленный на некоторой сетке. Для формирования двумерной прямоугольной сетки используется функция meshgrid(x,y), где x,y−одномерные массивы точек, задающие абсциссы и ординаты двумерной функции.

Пример. Построить поверхность .

>> x=0:0.2:8; y=0:0.2:4; [X, Y]=meshgrid(x, y); Z=2*cos(X+Y)+Y.*cos(X-Y); mesh(X, Y,Z)

Функция mesh() строит расцвеченную сетчатую поверхность, используя различную окраску вершин и рёбер.

Кроме функции mesh(), для изображения поверхности имеются и другие функции:

meshc()−строится сетчатая поверхность с линиями уровня;

meshz()−строится сетчатая поверхность и отсчётная плоскость;

surf()−строится расцвеченная поверхность;

surfc()−строится расцвеченная поверхность с линиями уровня;

surfl()−строится расцвеченная поверхность с подсветкой;

waterfall−строится поверхность без прорисовки ребер.

Пример. Построим поверхность этими функциями.

После построения рисунков для каждого рисунка можно выполнить масштабирование функцией axis([-Inf Inf —Inf Inf —Inf Inf]). Например, второй рисунок промасштабирует команда

При масштабировании определяются действительные интервалы изменения величин по всем координатам и рисунки становятся выразительнее.

1) Построить поверхность функцией на сетке x=0:0.2:8;y=0:0.2:4. Использовать режим вращения изображения для изменения ракурса. Режим вращения задаётся нажатием соответствующего значка на панели инструментов графического окна.

2) Эту же поверхность построить на более мелкой сетке x=0:0.05:8; y=0:0.05:4.

3) Эту же поверхность построить на сетке x=0:0.02:8;y=0:0.01:6

4) Построить поверхность функцией на сетке x=0:0.2:8; y=0:0.1:6

5) Выбрать сетку и построить поверхность функцией

6) Построить в одном графическом окне три поверхности : одну на сетке x=0:0.1:8;y=0:0.1:4, вторую на сетке x=0:0.05:8;y=0:0.05 и третью на сетке x=0:0.01:8;y=0:0.01:4.

7) Выбрать сетку и построить в одном графическом окне четыре поверхности при следующих значениях параметров и :

8) Построить в одном окне поверхность функциями и на сетке x=-pi:0.1:pi; y=-pi:0.1:pi. Выполнить масштабирование рисунков.

9) Построить поверхность функцией на сетке x=-pi:0.1:pi; y=-pi:0.1:pi. Установить единый масштаб по осям абсцисс и ординат, выбрать и установить ракурс, удалить сетку.

Источник

Некоторые полезные средства настройки графиков (plot) в MATLAB

Недавно, в очередной раз проверяя домашние работы своих студентов, я загорелся желанием автоматизировать этот процесс. Задание состояло в составлении рабочей таблицы девиации магнитного компаса и построения кривой девиации.

Входными данными служили показания магнитного компаса (МК), синхронно наблюдаемые показания гирокомпаса (ГК), поправка ГК и значение магнитного склонения для района, в котором проходили измерения.

Все данные были занесены в таблицу и разделены из 10 столбцов с входными данными и 25 строк – значений входных данных для каждого из вариантов. Для удобства считывания данных в MATLAB они были записаны в виде текстового файла и импортировались в рабочее пространство с помощью функции importdata.

По методике расчетов необходимо было обработать данные с помощью нескольких эмпирических формул для заполнения рабочей таблицы девиации МК. Однако, основным и наиболее наглядным результатом работы является построение кривой девиации МК.

Для построения графика была выбрана функция plot, имеющая большое количество параметров настройки, которые позволяют получить результат в нужном виде. Был составлен код:

И получен следующий график:

Разберем код построчно, рассмотрим какие параметры можно указывать для настройки отображения графиков.

Здесь задаются входные данные для построения графика. Количество значений по оси абсцисс и по оси ординат должно совпадать. По эти данные являются векторами с 36 значениями.

Собственно, функция построения графика, в которую передаются данные и параметры. Помимо очевидных входных данных параметром функции является тип отображаемой линии, закодированный трехсимвольным сочетанием. В данном случае “b” – blue, цвет линии; “o” – вид маркера, которым обозначаются точки графика и “-” – тип линии, в данном случае – сплошная.

Ниже привожу список параметров для настройки отображаемой линии.

Маркер Цвет линии
c голубой
m фиолетовый
y желтый
r красный
g зеленый
b синий
w белый
k черный

Маркер Тип линии
— непрерывная
— — штриховая
: пунктирная
-. штрих-пунктирная

Маркер Тип маркера
. точка
+ знак «плюс»
* знак «звездочка»
о круг
х знак «крест»

Команда, которой включается сетка на графике.

Подписи для графика и соответствующих осей. Здесь “\circ” кодировка символа градуса.

Команда управления осями. В данном случае выставлен параметр “auto” – автоматическая расстановка осей. Здесь-то меня и не устроила работа MATLAB, т.к. автоматически оси не пристыковывались к крайним значениям графика, а «добавляли» лишнее пространство по оси “X”.

С помощью команды “help axis” я нашел еще несколько вариантов параметра для осей, в частности попробовал параметр “tight”, который должен был пристыковывать границы графика к крайним значениям кривой. Однако результат и этого параметра меня не удовлетворил т.к. результат выглядел следующим образом:

График выглядит «зажатым», к тому же «теряются» части кривой находящиеся между максимальными значениями.

Для получения наглядного результата пришлось настроить ось “X” отдельно с помощью следующих команд:

Последняя функция задает граничные значения отдельно для оси “X”, что позволило мне ограничить график максимальными значениями по данной оси.

И последняя команда:

Позволила настроить подписи и шаг для оси “X”. Функция “set” является достаточно общей, ее работа зависит от передаваемых параметров. В данном случае “gca” – означает, что параметры будут устанавливаться для сетки графика, “ XTick ” – означает, что будет управляться подпись оси “X”, а параметр “0:45:360” – задает минимальное значение, шаг и максимальное значение.

В результате получился достаточно наглядный график кривой девиации, по сравнению формы которого с формой графика полученного студентом можно было быстро оценить правильность выполнения работы. Так же, благодаря загрузке данных из файла по всем вариантам, с дальнейшим выбором последнего, изменять приходилось только номер варианта, чтобы получить результат.

Надеюсь, что эта статья будет полезной не только для начинающих MATLAB, но и для опытных пользователей.

В окончании хотел бы отметить полезность команды “help” – она не только позволяет получить необходимую информацию по функции или команде из командной строки, но и сделать это значительно быстрее, чем через поиск в справке MATLAB.

Источник