Десятичная запись натуральных чисел что это
Понятие о натуральном числе
Натуральные числа и десятичная запись числа
Чтобы сосчитать некоторое количество предметов, используются числа, которые называют натуральными.
С помощью десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 можно записать любое натуральное число. (подобным образом мы используем буквы алфавита, чтобы записать слова)
Такую запись числа называют десятичной ‒ десять единиц каждого разряда составляют одну единицу следующего старшего разряда.
Натуральный ряд
Если натуральные числа записать в порядке возрастания, то получится ряд натуральных чисел ‒ натуральный ряд.
Каждое число в этом ряду меньше последующего на единицу. Наименьшее число среди натуральных чисел — это 1, а наибольшего числа нет.
Многозначные числа
Натуральное число называют однозначным, если его запись состоит из одного знака — одной цифры.
Например, числа 3, 7, 9 — однозначные.
Если запись числа состоит из двух знаков — двух цифр, то его называют двузначным.
Например, числа 25, 44, 65, 80 — двузначные.
Числа 100, 543, 888 — трёхзначные:
Числа 2000, 6791, 1060 — четырёхзначные и т. д.
Двузначные, трехзначные, четырёхзначные, пятизначные и т. д. — это многозначные числа.
Классы и разряды
Прочитать записи однозначных, двузначных и трехзначных чисел (например: 7, 54, 976) затруднений не вызывает.
Чтобы прочесть многозначное натуральное число, его необходимо разбить справа налево на группы по три цифры в каждой. Крайняя левая группа может состоять из одной или двух цифр.
Эти группы называют классами.
Три первые цифры справа ‒ это класс единиц, три следующие — класс тысяч, затем класс миллионов, класс миллиардов и т. д.
Место, занимаемое цифрой в записи числа, называют разрядом.
Если считать справа налево, то первое место в записи числа называют разрядом единиц, второе — разрядом десятков, третье — разрядом сотен и т. д.
Например, в числе 5034 имеем 4 единицы разряда единиц, 3 единицы разряда десятков, 0 единиц разряда сотен и 5 единиц разряда тысяч.
Можно также сказать, что в классе единиц 34 единицы.
Названия некоторых больших чисел
1 тысяча (1 тыс.) – 1 000 (тысяча)
1 миллион (1 млн) – 1 000 000 (тысяча тысяч)
1 миллиард (1 млрд) – 1 000 000 000 (тысяча миллионов)
1 триллион (1 трлн) – 1 000 000 000 000 (тысяча миллиардов)
Рассмотрим число 6 000 126 754.
Его читают: 6 миллиардов 126 тысяч семьсот пятьдесят четыре.
В классе миллионов во всех разрядах стоят нули. Поэтому при чтении числа 6 000 126 754 не произносят название этого класса.
Примеры прочтения чисел:
а) Число 200 700 читается так: двести тысяч семьсот;
б) Число 6 000 008 читается так: шесть миллионов восемь;
в) Число 14 000 002 000 читается так: четырнадцать миллиардов две тысячи.
Значение цифры в записи числа
Значение цифры зависит от её позиции (места) в записи числа.
Например, в записи числа 56 978 цифра 8 означает 8 единиц, так как она стоит на последнем месте в записи числа (в разряде единиц);
В записи числа 42 389 цифра 8 означает 8 десятков, так как она стоит на предпоследнем месте в записи числа (в разряде десятков);
В записи числа 5 300 847 цифра 8 означает 8 сотен, так как она стоит на третьем месте от конца в записи числа (в разряде сотен).
Число 0 и цифра 0
Число 0 натуральным не является.
Цифра 0 означает отсутствие единиц данного разряда в десятичной записи числа. Она служит и для обозначения числа «нуль» (что означает ‒ «ни одного»).
(Например, счёт 1 : 0 хоккейного матча говорит о том, что вторая команда не забила ни одной шайбы в ворота противника.)
Поделись с друзьями в социальных сетях:
Десятичная запись натуральных чисел что это
*Заочная математическая школа
Составитель преподаватель КубГУ Соколова И.В.
Тема 1. Десятичная запись натурального числа.
Первые представления о числе приобретены людьми с незапамятной древности. Они возникли изсчета людей, животных, плодов, различных изделий человека и других предметов. Результатом счета являются числа 1, 2, 3, 4, 5,… Этот ряд продолжается без конца; он называется натуральным рядом, а числа–натуральными.
Способы записи чисел называют системами счисления. Нашу систему счисления называют позиционной, т.к. каждая из цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) имеет различное значение в зависимости от позиции цифры в записи числа. Например, каждая цифра 3 в записи числа 333 имеет различное числовое значение: первая слева обозначает 3 сотни, вторая – 3 десятка, третья – 3 единицы. За основание нашей системы счисления взято число 10, поэтому она называется десятичной.
Любое натуральное число в десятичной системе счисления можно записать в виде суммы числа единиц, десятков, сотен и т.д. Например, запись 27 354 выражает, что в составе числа имеются 4 единицы, 5 десятков, 3 сотни, 7 тысяч и 2 десятка тысяч. В виде суммы оно запишется так:
27 354=2 · 10 000 + 7 · 1 000 + 3 · 100 + 5 · 10 + 4.

Двузначное число разделили на его первую цифру. В результате получили 14. Найти все такие двузначные числа.
У трехзначного числа поменяли местами последние 2 цифры. В результате число уменьшилось на 18. Найдите это число.
Тема 2. Деление с остатком.
Известно, что всякое натуральное число a можно разделить на другое натуральное число b с остатком, т.е. единственным образом представить a в виде:
В страну Арифметику прибыла “делегация” чисел, при делении которых на 11 получались частные равные остаткам. Какой вид имели эти числа и сколько их было?
Тема 3. Правила нахождения остатков.
Рассмотрим правила нахождения остатков при делении натуральных чисел на 2, 3, 4, 5, 10, 25:
1. Число делится на 2 (на 5, на 10), если его последняя цифра делится на 2 (на 5, на 10);
2. Число делится на 4 (на 25), если число, записанное двумя его последними цифрами, делится на 4 (на 25);
3. Число делится на 3 (на 9), если сумма его цифр делится на 3 (на 9).
Упражнение 2. Получить указанные правила на примере делимости трехзначных чисел.
Решение. Воспользуемся свойством: если 


1. 

2. 


3.



Сформулируйте признаки делимости чисел на 2, 3, 4, 5, 10, 25.
Упражнение 3. Докажите, что если в трехзначном числе средняя цифра равна сумме крайних, то число делится на 11.
Решение. Если цифры числа (слева направо) a, a+b, b, то само число: 
Получили, что в разложении числа на множители есть 11, следовательно, число делится на 11.
Из трех различных цифр, отличных от нуля составили всевозможные двузначные числа так, что цифры в записи числа не повторялись. Докажите, что сумма всех полученных чисел делится на 22 независимо от исходного выбора цифр.
Докажите, что число 
Если натуральные числа a и b делятся на некоторое натуральное число d, то d называется их общим делителем. Наибольший из общих делителей называется их наибольшим общим делителем и обозначается НОД(a, b). Если НОД(a, b)=1, то числа a и b называют взаимно простыми.
Упражнение 4. Найти все пятизначные числа вида 34x5y, каждое из которых делится на 36.
Решение. Число 36 можно представить в виде произведения взаимно простых чисел 9 и 4, следовательно, искомые числа делятся на 4 и 9. Число 5y должно делиться на 4, значит y=2 или y=6. 3+4+x+5+y=12+x+y должно делится на 9. При y=2 находим такую цифру x, чтобы 

Чтобы получить доступ к секретной информации компьютера, необходимо набрать код – четырехзначное число. Известно, что 1-я и 3-я цифра кода – единицы, а все число делится на 15, но не делится на 2. Найдите минимальное количество кодов, которые нужно перебрать, чтобы обнаружить искомый код.
Тема 4. Алгоритм Евклида.
Для разыскания НОД чисел применяется и другой метод. Он называется алгоритмом Евклида. Познакомимся с алгоритмом Евклида на примерах.
а) НОД(6621,111); б) НОД(40,5).
а) Делим 6621 на 111 с остатком:
Теперь делим делитель 111 на остаток 72:
Снова делим делитель на остаток и т.д.
Процесс закончен, если на некотором шаге получаем остаток, равный нулю. НОД данных чисел равен последнему отличному от нуля остатку в алгоритме Евклида. В нашем случае это 3, т.е. НОД(6621,111)=3. Процесс, описанный в алгоритме Евклида не бесконечен, так как остатки убывают, оставаясь неотрицательными, а самый маленький из них ноль: 72>39>33>6>3>0=0.
б) Разделим 40 на 5: 40=5·8+0. На первом шаге получили остаток 0. В этом случае НОД(40,5) равен меньшему из чисел, т.е. 5.
Если натуральное число k делится на числа a и b, то оно называется общим кратным чисел a и b. Наименьшее из таких общих кратных называется наименьшим общим кратным чисел a и b и обозначается НОК(a, b).
НОК двух чисел равно их произведению, деленному на их НОД, т.е.

Пользуясь алгоритмом Евклида, найдите НОД и НОК номера вашего дома и почтового индекса.
Из победителей математической олимпиады был сформирован отряд, в котором больше 100, но меньше 150 детей. Для отправки в летнюю математическую школу их разместили вначале в 8, а затем в 10 автобусах. При этом в обоих случаях детей в автобусах оказалось поровну. Сколько в отряде было девочек и мальчиков, если девочек было на 40 человек меньше, чем мальчиков?
Для учеников трех шестых классов школа к новогоднему вечеру закупила шоколадные конфеты: 390, 405 и 420 штук. Сколько подарков получил каждый класс, если в каждом подарке одинаковое количество конфет и число их – наибольшее из всех возможных.
а) 


Даны две равные дроби. Одна из них 
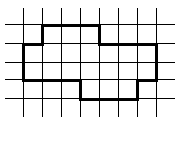
Укажите различные способы разрезания данной фигуры на 4 равные части, чтобы линия разреза шла по сторонам клеток. (Способы считаются различными, если части, получаемые при одном способе разрезания не равны частям, полученным при другом способе).
Натуральные числа
Определение натурального числа
Натуральные числа — это числа, которые мы используем для подсчета чего-то конкретного, осязаемого.
Вот какие числа называют натуральными: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, …
Натуральный ряд — последовательность всех натуральных чисел, расположенных в порядке возрастания. Первые сто можно посмотреть в таблице.
Какие операции возможны над натуральными числами
Записывайтесь на курсы обучения математике для учеников с 1 по 11 классы!
Десятичная запись натурального числа
В школе мы проходим тему натуральных чисел в 5 классе, но на самом деле многое нам может быть интуитивно понятно и раньше. Проговорим важные правила.
Мы регулярно используем цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. При записи любого натурального числа можно использовать только эти цифры без каких-либо других символов. Записываем цифры одну за другой в строчку слева направо, используем одну высоту.
Примеры правильной записи натуральных чисел: 208, 567, 24, 1 467, 899 112. Эти примеры показывают нам, что последовательность цифр может быть разной и некоторые даже могут повторяться.
077, 0, 004, 0931 — это неправильные примеры натуральных чисел, потому что ноль расположен слева. По правилам так нельзя. Это и есть десятичная запись натурального числа.
Количественный смысл натуральных чисел
Натуральные числа несут в себе количественный смысл, то есть выступают в качестве инструмента для нумерации.
Представим, что перед нами банан 🍌. Мы можем записать, что видим 1 банан. При этом натуральное число 1 читается как «один» или «единица».
Но термин «единица» имеет еще одно значение: то, что можно рассмотреть, как единое целое. Элемент множества можно обозначить единицей. Например, любое дерево из множества деревьев — единица, любой листок из множества листков — единица.
Представим, что перед нами 2 банана 🍌🍌. Натуральное число 2 читается как «два». Далее, по аналогии:
| 🍌🍌🍌 | 3 предмета («три») |
| 🍌🍌🍌🍌 | 4 предмета («четыре») |
| 🍌🍌🍌🍌🍌 | 5 предметов («пять») |
| 🍌🍌🍌🍌🍌🍌 | 6 предметов («шесть») |
| 🍌🍌🍌🍌🍌🍌🍌 | 7 предметов («семь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌 | 8 предметов («восемь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌🍌 | 9 предметов («девять») |
Основная функция натурального числа — указать количество предметов.
Если запись числа совпадает с цифрой 0, то его называют «ноль». Напомним, что ноль — не натуральное число, но он может обозначать отсутствие. Ноль предметов значит — ни одного.
Однозначные, двузначные и трехзначные натуральные числа
Однозначное натуральное число — это такое число, в составе которого один знак, одна цифра. Девять однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Двузначные натуральные числа — те, в составе которых два знака, две цифры. Цифры могут повторяться или быть различными. Например: 88, 53, 70.
Если множество предметов состоит из девяти и еще одного, значит, речь идет об 1 десятке («один десяток») предметов. Если один десяток и еще один, значит, перед нами 2 десятка («два десятка») и так далее.
По сути, двузначное число — это набор однозначных чисел, где одно записывается справа, а другое слева. Число слева показывает количество десятков в составе натурального числа, а число справа — количество единиц. Всего двузначных натуральных чисел — 90.
Трехзначные натуральные числа — числа, в составе которых три знака, три цифры. Например: 666, 389, 702.
Одна сотня — это множество, состоящее из десяти десятков. Сотня и еще одна сотня — 2 сотни. Прибавим еще одну сотню — 3 сотни.
Вот как происходит запись трехзначного числа: натуральные числа записываются одно за другим слева направо.
Крайнее правое однозначное число указывает на количество единиц, следующее — на количество десятков, крайнее левое — на количество сотен. Цифра 0 показывает отсутствие единиц или десятков. Поэтому 506 — это 5 сотен, 0 десятков и 6 единиц.
Точно так же определяются четырехзначные, пятизначные, шестизначные и другие натуральные числа.
Многозначные натуральные числа
Многозначные натуральные числа состоят из двух и более знаков.
1 000 — это множество с десятью сотнями, 1 000 000 состоит из тысячи тысяч, а один миллиард — это тысяча миллионов. Тысяча миллионов, только представьте! То есть мы можем рассмотреть любое многозначное натуральное число как набор однозначных натуральных чисел.
Например, 2 873 206 содержит в себе: 6 единиц, 0 десятков, 2 сотни, 3 тысячи, 7 десятков тысяч, 8 сотен тысяч и 2 миллиона.
Сколько всего натуральных чисел?
Однозначных 9, двухзначных 90, трехзначных 900 и т.д.
Свойства натуральных чисел
Об особенностях натуральных чисел мы уже знаем. А теперь подробно расскажем про их свойства:
| множество натуральных чисел | бесконечно и начинается с единицы (1) |
| за каждым натуральным числом следует другое | оно больше предыдущего на 1 |
| результат деления натурального числа на единицу (1) | само натуральное число: 5 : 1 = 5 |
| результат деления натурального числа на него самого | единица (1): 6 : 6 = 1 |
| переместительный закон сложения | от перестановки мест слагаемых сумма не меняется: 4 + 3 = 3 + 4 |
| сочетательный закон сложения | результат сложения нескольких слагаемых не зависит от порядка действий: (2 + 3) + 4 = 2 + (3 + 4) |
| переместительный закон умножения | от перестановки мест множителей произведение не изменится: 4 × 5 = 5 × 4 |
| сочетательный закон умножения | результат произведения множителей не зависит от порядка действий; можно хоть так, хоть эдак: (6 × 7) × 8 = 6 × (7 × 8) |
| распределительный закон умножения относительно сложения | чтобы умножить сумму на число, нужно каждое слагаемое умножить на это число и полученные результаты сложить: 4 × (5 + 6) = 4 × 5 + 4 × 6 |
| распределительный закон умножения относительно вычитания | чтобы умножить разность на число, можно умножить на это число отдельно уменьшаемое и вычитаемое, а затем из первого произведения вычесть второе: 3 × (4 − 5) = 3 × 4 − 3 × 5 |
| распределительный закон деления относительно сложения | чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные результаты: (9 + 8) : 3 = 9 : 3 + 8 : 3 |
| распределительный закон деления относительно вычитания | чтобы разделить разность на число, можно разделить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе: (5 − 3) : 2 = 5 : 2 − 3 : 2 |
Разряды натурального числа и значение разряда
Напомним, что от позиции, на которой стоит цифра в записи числа, зависит ее значение. Так, например, 1 123 содержит в себе: 3 единицы, 2 десятка, 1 сотню, 1 тысячу. При этом можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен и 1 служит значением разряда тысяч.
Разряд — это позиция, место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще — чтобы визуально разделить разные классы чисел.
Класс — это группа разрядов, которая содержит в себе три разряда: единицы, десятки и сотни.
Десятичная система счисления
Люди в разные времена использовали разные методы записи чисел. И каждая система счисления имеет свои правила и особенности.
Десятичная система счисления — самая распространенная система счисления, в которой для записи чисел используют десять знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
В десятичной системе значение одной и той же цифры зависит от ее позиции в записи числа. Например, число 555 состоит из трех одинаковых цифр. В этом числе первая слева цифра означает пять сотен, вторая — пять десятков, а третья — пять единиц. Так как значение цифры зависит от ее позиции, десятичную систему счисления называют позиционной.
Вопрос для самопроверки
Сколько натуральных чисел можно отметить на координатном луче между точками с координатами: