Действия второй ступени в математике что это
Порядок действий в математике
Основные операции в математике
Порядок вычисления простых выражений
Есть однозначное правило, которое определяет порядок выполнения действий в выражениях без скобок:
Из этого правила становится яснее, какое действие выполняется первым. Универсального ответа нет, нужно анализировать каждый пример и подбирать ход решения самостоятельно.
Что первое, умножение или деление? — По порядку слева направо.
Сначала умножение или сложение? — Умножаем, потом складываем.
Порядок выполнения действий в математике (слева направо) можно объяснить тем, что в нашей культуре принято вести записи слева направо. А необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Рассмотрим порядок арифметических действий в примерах.
Пример 1. Выполнить вычисление: 11- 2 + 5.
В нашем выражении нет скобок, умножение и деление отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычтем два из одиннадцати, затем прибавим к остатку пять и в итоге получим четырнадцать.
Вот запись всего решения: 11- 2 + 5 = 9 + 5 = 14.
Пример 2. В каком порядке выполнить вычисления в выражении: 10 : 2 * 7 : 5?
Чтобы не ошибиться, перечитаем правило для выражений без скобок. У нас есть только умножение и деление — значит сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Сначала выполняем деление десяти на два, результат умножаем на семь и получившееся в число делим на пять.
Запись всего решения выглядит так: 10 : 2 * 7 : 5 = 5 * 7 : 5 = 35 : 5 = 7.
Пока новые знания не стали привычными, чтобы не перепутать последовательность действий при вычислении значения выражения, удобно над знаками арифметический действий расставить цифры, которые соответствуют порядку их выполнения.
Например, в такой последовательности можно решить пример по действиям:
Действия первой и второй ступени
В некоторых учебниках по математике можно встретить разделение арифметических действий на действия первой и второй ступени.
С этими терминами правило определения порядка выполнения действий звучит так:
Если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем — действия первой ступени (сложение и вычитание).
Порядок вычислений в выражениях со скобками
Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:
Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.
Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.
Рассмотрим порядок выполнения действий на примерах со скобками.
Как правильно решить пример:
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.
Подставляем полученные значения в исходное выражение:
Порядок действий: умножение, деление, и только потом — сложение. Получится:
10 + 2 * 8 : 2 = 10 + 16 : 2 = 10 + 8 = 18.
На этом все действия выполнены.
Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.
Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).
Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:
Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:
5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.
Исходное значение, после подстановки примет вид 9 + 26, и остается лишь выполнить сложение: 9 + 26 = 35.
Ответ: 9 + (5 + 1 + 4 * (2 + 3)) = 35.
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции — их значения нужно вычислить до выполнения остальных действий. При этом важно учитывать правила из предыдущих пунктов, которые задают очередность действий в математике.
Другими словами, перечисленные функции по степени важности можно приравнивать к выражению в скобках.
И, как всегда, рассмотрим, как это работает на примере.
В этом выражении есть степень 62. И нам нужно найти ее значение до выполнения остальных действий. Выполним возведение в степень: 62 = 36.
Подставляем полученное значение в исходное выражение:
Дальше нам уже все знакомо: выполняем действия в скобках, далее по порядку слева направо выполняем сначала умножение, деление, а затем — сложение и вычитание. Ход решения выглядит так:
Закрепить на практике тему «Порядок действий» можно на курсах по математике в Skysmart!
Порядок выполнения действий, правила, примеры
Когда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий. Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.
В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.
Порядок вычисления простых выражений
В случае выражений без скобок порядок действий определяется однозначно:
Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.
Решение
В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:
Решение
Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.
Решение
17 − 5 · 6 : 3 − 2 + 4 : 2 = 17 − 10 − 2 + 2
Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:
17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7
Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:
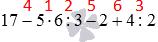
Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.
Что такое действия первой и второй ступени
Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.
К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.
Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:
В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).
Порядок вычислений в выражениях со скобками
Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:
Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.
Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.
Решение
Теперь нам нужно подставить получившиеся значения в первоначальное выражение:
5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 5 + 1 · 2 : 2
Начнем с умножения и деления, потом выполним вычитание и получим:
5 + 1 · 2 : 2 = 5 + 2 : 2 = 5 + 1 = 6
На этом вычисления можно закончить.
Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.
Решение
Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.
Разберем пример такого вычисления.
Решение
Дальше действуем по знакомому алгоритму: считаем, сколько у нас получится в скобках, потом в оставшемся выражении выполняем умножение и деление, а следом – сложение и вычитание.
( 3 + 1 ) · 2 + 36 : 3 − 7 = 4 · 2 + 36 : 3 − 7 = 8 + 12 − 7 = 13
В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.
Действия первой и второй ступени
Арифметические действия делятся на действия первой и второй ступени.
Порядок действий
Если выражение содержит действия только одной ступени и в нём нет скобок, то действия выполняются в порядке их следования слева направо.
Пример 1. Вычислить значение выражения:
Решение: Данное выражение содержит действия только одной ступени — первой (сложение и вычитание). Надо определить порядок действий и выполнить их.
| 1 | 2 | 3 | 4 | |||||
|---|---|---|---|---|---|---|---|---|
| 15 | + | 17 | — | 20 | + | 8 | — | 12 |
Пример 2. Вычислить значение выражения:
Решение: Данное выражение содержит действия только одной ступени — второй (умножение и деление). Надо определить порядок действий и выполнить их.
| 1 | 2 | 3 | 4 | |||||
|---|---|---|---|---|---|---|---|---|
| 60 | : | 15 | · | 7 | : | 2 | · | 3 |
Если выражение содержит действия обеих ступеней, то первыми выполняются действия второй ступени, в порядке их следования (слева направо), а затем действия первой ступени.
Пример. Вычислить значение выражения:
Решение: Данное выражение содержит четыре действия: два первой ступени и два второй. Определим порядок их выполнения: согласно правилу первым действием будет деление, вторым — умножение, третьим — сложение, а четвёртым — вычитание.
Математика. 5 класс
Настройка зачисления на курс
Математика. 5 класс
Навигация
Детский технопарк «Кванториум»
История и обществознание
Основы безопасности жизнедеятельности
МОУ «Лицей прикладных наук»
МУДО «Центр дополнительного образования»
МОУ «Прогимназия № 237 «Семицветик»
МУ ДО «Центр детского творчества»
Олимпиада_Информатика и ИКТ
МАУ ДО «Центр дополнительного образования для детей»
МАДОУ «ДС № 236 Лукоморье»
МУДО «Детско-юношеский центр»
МУДО «Центр детского творчества»
ОУ городского подчинения и ГБУ
Ассоциация попечителей образования
МАОУ «Физико-технический лицей № 1»
МУДО «Центр туризма, краеведения и морской подгото.
МАУ ДО «Дворец творчества детей и молодежи»
МБОУ СОШ с. Новоалександровка им. Героя Советско.
МБОУ СОШ№ 1 с.Александров-Гай Саратовской области
МБОУ ДО «ЦДТ» с. Александров-Гай Александрово-Гайс.
МОУ-СОШ села Марфино Аткарского района
МАОУ Гимназия №2 г.Балаково
МАОУ «ООШ № 10» г. Балаково
МАОУ СОШ №13 г. Балаково
МАУДО ЦДО г. Балаково
МБУДО Центр «Созвездие» г. Балашов
МОУ «СОШ с. Черкасское»
МОУ «СОШ №11» г. Вольск
ГАПОУ СО «Вольский педагогический колледж им. Ф.И.
МУДО ВМР «ЦДО «Радуга»
МОУ «СОШ с. Воскресенское»
МОУ «СОШ с. Синодское»
МОУ «ООШ с. Верхазовка»
МОУ «СОШ п. Первомайский»
МУДО «Дом детского творчества»
МОУ «СОШ им. Г.И. Марчука р.п. Духовницкое»
МОУ «СОШ имени Н.В. Грибанова с. Брыковка»
МОУ СОШ с. Андреевка
МБОУ «Дом детского творчества»
МОУ «СОШ с. Ивантеевка»
МУ ДО «Дом детского творчества»
МБУ ДО «Детско-юношеская спортивная школа г. Калин.
МБОУ «СОШ с.Симоновка Калининского района Саратовс.
МБУ ДО «Дом детского творчества г. Калининска Сара.
МБОУ «СОШ с. Колокольцовка»
МБОУ «СОШ с.Симоновка»
МБОУ «СОШ № 11 с. Золотое»
МБУДО «ЦТОТД и М г.Красноармейска»
МОУ «СОШ с.Логиновка»
МУ ДО «Районный Дом детского творчества р.п. Горный «
МБОУ «СОШ № 2 р.п. Лысые Горы»
МОУ «СОШ № 1 р.п. Лысые Горы»
МБОУ «СОШ с. Широкий Карамыш»
МБОУ «СОШ с. Большая Рельня»
МБУ ДО «ЦДОД» р.п. Лысые Горы
МБОУ «ООШ с. Юнгеровка»
МБОУ «СОШ с. Двоенки»
МБОУ «СОШ с. Атаевка»
МБОУ «СОШ с. Бутырки»
МБОУ «СОШ п. Яблочный»
МБОУ «СОШ п. Октябрьский»
МБОУ «СОШ с. Невежкино»
МОУ СОШ с. Подлесное
МОУ «СОШ с. Павловка»
МОУ «СОШ с. Кировское»
МБОУ-СОШ №6 г. Маркса
МОУ «СОШ № 4» г. Маркса
МОУ СОШ с. Звонаревка
МОУ-СОШ с Орловское
МУ ДО – Центр внешкольной работы
МОУ «СОШ п. Динамовский
МОУ «СОШ с. Гремячка»
МУ ДО «ДДТ г. Новоузенска»
Метапредметный курс «Биология + Химия»
МОУ «СОШ п. Сланцевый рудник»
МОУ «Школа с. Новочерниговка»
МБУДО «Дом детского творчества р.п. Озинки»
МБОУ «СОШ с. Н. Покровка»
МБОУ «СОШ с.Натальин Яр»
МБОУ «СОШ с.Грачев Куст»
МБОУ «СОШ имени М.М. Рудченко»
МБУ ДО «Детско-юношеский центр» г. Петровск
МБУДО «Детско-юношеская спортивная школа имени Т.В.
МБУДО «ДОООЦ «ДЕЛЬФИН» г. Петровск
МУ ДО «Дом детского творчества»
МОУ «СОШ №14 г. Пугачёва им. П.А.Столыпина»
МОУ СОШ с. Старая Порубёжка
МОУ «СОШ с. Заволжский»
МОУ «СОШ №2 г. Пугачева»
МОУ «СОШ № 13 г. Пугачева Саратовской области имен.
МБУ ДО «Центр развития творчества детей и юношеств.
МБОУ «СОШ с. Скатовка»
МБУ ДО «Дом детского творчества р.п.Ровное»
МОУ«СОШ с. Багаевка им. Н.В. Котлова»
МОУ «СОШ с.Березина Речка»
МОУ «СОШ с. Синенькие»
МОУ «СОШ р.п. Соколовый»
МОУ «СОШ с.Усть-Курдюм»
МУ ДО «ЦДТ р.п. Самойловка»
МБОУ «СОШ №1» р.п. Степное
МБОУ «СОШ р.п. Пушкино»
МБУ ДО-РДДиЮ Советского района.
МОУ «СОШ с. Сторожевка»
МОУ «СОШ с. Мизино-Лапшиновка
МОУ «СОШ с. Ягодная Поляна»
МОУ «Татищевский лицей»
МОУ «СОШ с. Октябрьский Городок»;
МОУ СОШ № 1 г. Хвалынска
МОУ ДО «ДДТ «Хвалынский»
Звуковая культура речи
Трудовое обучение(технический труд)
Информатика, физика, астрономия
МОУ «СОШ №30 им. П. М. Коваленко»
МАУ ДО «Дворец творчества детей и молодежи»
МУ ДО «Центр «Позитив»
МОУ «СОШ п. Пробуждение»
МБОУ «СОШ с. Генеральское»
МОУ «СОШ «Патриот» с кадетскими классами»
МОУ «ООШ с. Квасниковка»
МОУ «СОШ п. им. К Маркса»
МОУ «ООШ с. Ленинское»
МОУ «СОШ с.Широкополье»
МОУ «СОШ с. Зеленый Дол»
МОУ «ООШ с. Титоренко»
МБОУ «СОШ с Красный Яр
ГАПОУ СО «Энгельсский политехникум»
МБОУ «СОШ с. Старицкое»
МОУ «СОШ п. Коминтерн»
МОУ «СОШ с.Воскресенка»
МОУ «СОШ №12 г. Шиханы»
МУ ДО ЗАТО Светлый
МОУ СОШ №3 им. В.Н. Щеголева
МОУ «СОШ №2 им. В.А. Коновалова»
МБУ ДО «Дом детского творчества Балтайского района
Дистанционное обучение детей-инвалидов
Мероприятия для МЦДОДИ
Российские цифровые образовательные платформы
15-16.11.2021Семинар «Дистанционные формы обучения.
Семинар 7 октября 2021
Семинар 18,19 декабря 2020
Курсы для преподавателей
Образовательная сессия 18-20.11.2020
Семинар 20 августа 2020
МАУДО «ЦДТ» Кировский район
МБУ ДО «ДДТ г. Калининск»
МОУ «СОШ с. Клещевка»
МОУ СОШ п. Возрождение
МУ ДО «Дом пионеров и школьников» Романовка
МБУ ДО «ЦРТДЮ» г. Пугачев
МУДО ЦДТ «Светлячок» г. Ртищево
Семинар 19-20 марта 2020
Обучающие семинары для СПО
Семинар для СПО (Базарный Карабулак)
Семинар 18, 20 декабря 2019 года
Семинар «Разработка дистанционного курса в СДО Moo.
Дополнительное образование 23.09.2019
Семинар 27 марта 2019 года
Региональный Краеведческий марафон «Саратовская кр.
Областной конкурс видео и дистанционных курсов «До.
Консультационный центр конкурса «Доступное образо.
Виртуальный исторический класс
Методическое объединение дистанционных педагогов
Действия второй ступени в математике что это
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту
В этом уроке познакомимся с правилом порядка выполнения действий в выражении, узнаем, какие действия относятся к действиям первой ступени, а какие – к действиям второй ступени.
75 : 5 + 30 ∙ 2 – 56 : 7
В данном выражении нужно выполнить 5 действий: два деления, сложение, вычитание и умножение.
В математике действия сложение и вычитание называют действиями первой ступени. Легко запомнить, с этими действиями мы знакомимся сначала изучения математики, еще в первом классе.
Умножение и деление называют действиями второй ступени.
Чтобы найти значение заданного выражения, нужно сначала выполнить действия второй ступени, а потом с их результатами выполнить действия первой ступени.
Заметим, что действия одной и той же ступени выполняются по порядку слева направо. Итак:
первое действие второй ступени – деление 75 : 5 = 15,
второе действие – умножение 30 ∙ 2 = 60,
третье действие 56 : 7 = 8.
Выполнили все действия второй ступени слева направо.
Переходим к действиям первой ступени.
Их тоже выполняем слева направо.
15 + 60 = 75, 75 – 8 = 67.
Значение выражения 67.
Найдем значение еще одного выражения:
В данном выражении тоже действия первой и второй ступени.
Но оно отличается от первого выражения тем, что в нем есть скобки.
В таком случае вначале выполняются действия в скобках, сначала в первых скобках:
потом во вторых скобках 15 + 5 = 20.
После этого выполняем действие вне скобок с результатами, которые получились в скобках:
Подведем итоги: сформулируем правило порядка выполнения действий в выражении.
Сначала выполняются действия в скобках.
Потом выполняются действия второй ступени (умножение или деление) по порядку слева направо.
Последними выполняются действия первой ступени (сложение и вычитание) по порядку слева направо.
В этом уроке Вы познакомились с правилом порядка выполнения действий в выражении, в которых есть действия первой и второй ступени.


