Диаграмма рассеяния для чего
Диаграмма разброса
Применяется диаграмма разброса в том случае, когда необходимо отобразить что происходит с одной переменной при изменении другой, для определения причины возникновения неконтролируемых точек в ходе многовариантного статистического контроля процесса, подтверждения взаимосвязи, выявленной в результате применения причинно-следственной диаграммы (диаграммы Исикавы) и пр.
Диаграмма разброса строится в следующей последовательности:
1. Собираются парные данные, которые по предположению являются взаимосвязанными. Желательно, чтобы таких парных данных было не менее 20-25. Это позволит более объективно установить зависимость между данными.
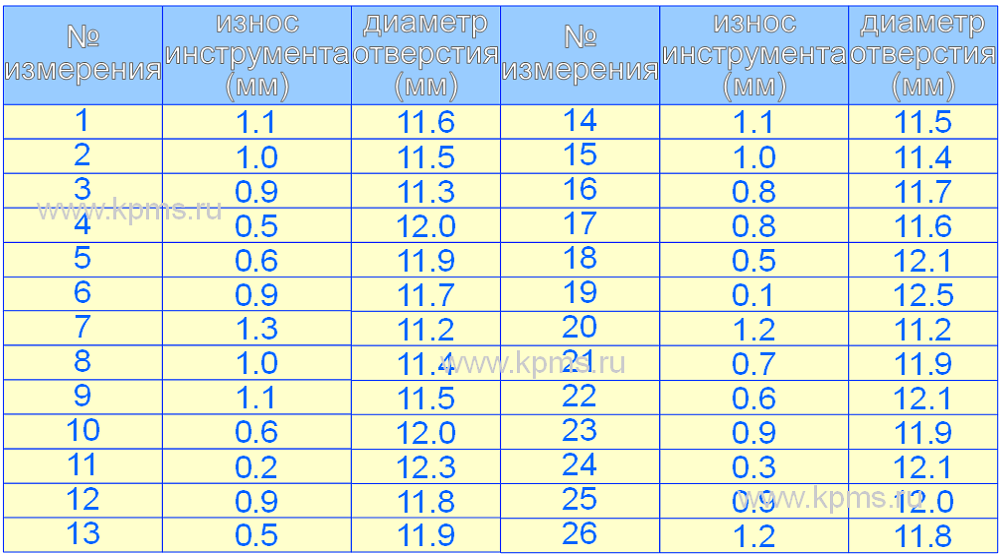
2. Составляется список данных. В списке данных для каждого измерения по порядку указываются значения парных данных.
3. Определяются максимальные и минимальные значения по каждому из типов парных данных.
4. Выбираются шкалы для осей диаграммы разброса на основании разницы между максимальным и минимальным значением каждого из типов парных данных. При необходимости (если отображаемые величины имеют малые размеры) могут применяться коэффициенты масштабирования шкалы.
6. На диаграмму наносятся парные данные. Если для разных измерений получаются одинаковые значения данных, то для отделения данных друг от друга используется другое обозначение (например, точки и треугольники) или данные обозначаются рядом друг с другом.
Пример
Диаграмма разброса построена для парных данных – «износ инструмента» и «диаметр отверстия». Данные собирались, чтобы показать влияние износа инструмента на диаметр отверстия. Как предполагалось, чем больше износ инструмента, тем меньше должен быть диаметр отверстия.
Величина шкалы, на которой будут отображаться данные – 1,2 мм. Для отображения данных на диаграмме применим коэффициент масштабирования 10.
Величина шкалы, на которой будут отображаться данные – 1,7 мм. Для отображения данных на диаграмме применим коэффициент масштабирования 10.
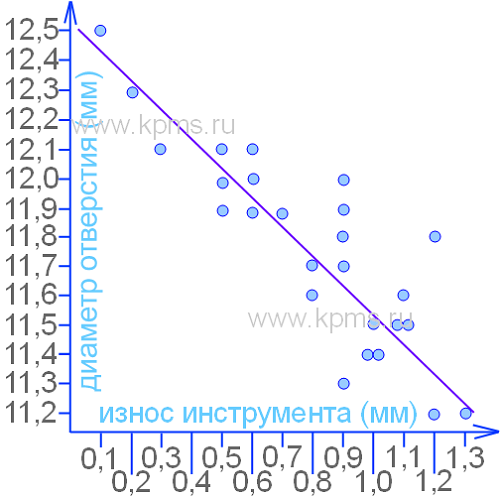
Между точками на графике можно провести прямую линию, вдоль которой они концентрируются. Это свидетельствует о корреляции между исследуемыми парными данными. Диаграмма разброса показывается величину и наличие взаимосвязи между двумя переменными. Направление и «сжатость» кластера точек говорит о виде и силе взаимосвязи между двумя переменными. Чем больше этот кластер имеет сходство с прямой линией, тем сильнее корреляция между парными данными.
На основании проведенного анализа, который предоставляет диаграмма разброса, можно принимать дальнейшие решения. В частности, для приведенного примера можно установить допустимый предел износа инструмента в зависимости от разрешенного допуска на диаметр отверстия.
Варианты корреляции
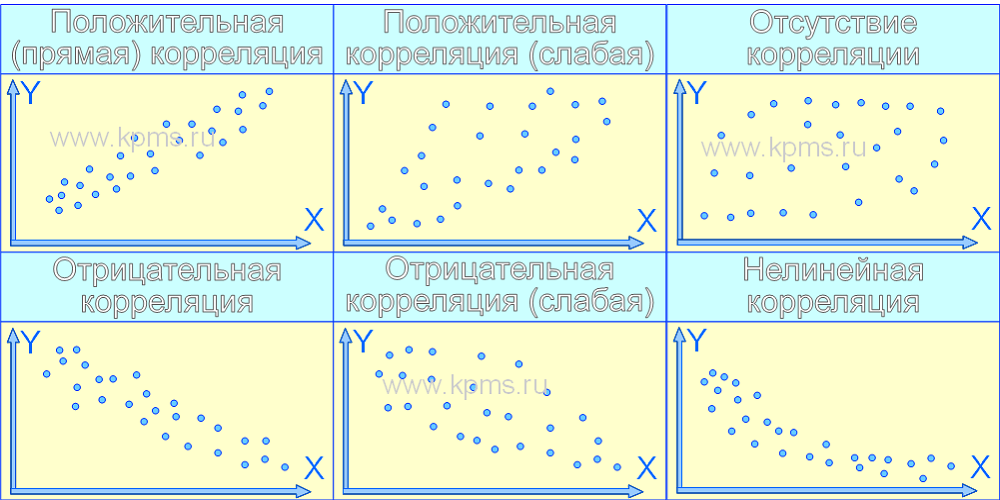
Форма и расположение кластера точек на диаграмме разброса определяют различные варианты корреляции парных данных. Наиболее часто встречающиеся из них приведены на рисунках ниже.
Диаграмма разброса является удобным и простым инструментом для выявления взаимосвязи парных данных. Однако сильная взаимосвязь не обязательно означает, что одна переменная напрямую связана с другой переменной. В частности, может быть третья переменная, которая влияет на исследуемые парные данные и которая в итоге «кластеризует» точки на диаграмме разброса.
Инструмент «диаграмма разброса» входит в состав сборника «Семь инструментов качества». Сборник можно приобрести в интернет-магазине «Менеджмент качества».
Семь инструментов качества
Семь инструментов качества
Брошюра «Семь инструментов качества» содержит справочную информацию об основных инструментах менеджмента качества. В брошюре представлено описание и даны примеры применения следующих инструментов менеджмента качества:
Инструменты качества: диаграмма рассеяния
Опубликовано: 1.07.2014 Рубрика: Статьи Автор: Единый Стандарт
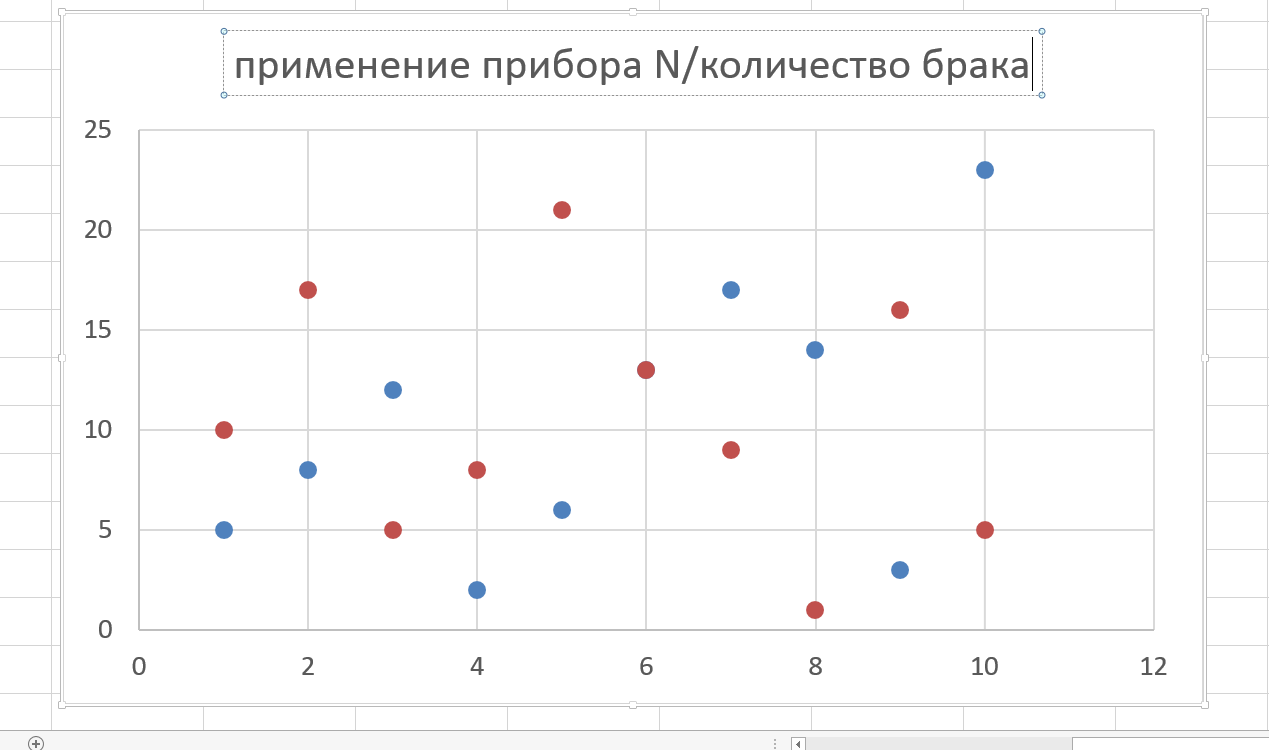
Эта диаграмма помогает наглядно представить зависимость между двумя типами данных. Она может быть полезна, например, когда требуется лучше понять зависимость качества продукции от того или иного существующего фактора. Диаграмму рассеяния можно построить и на бумаге, но сегодня для этого чаще используется программное обеспечение, хорошо подходит Excel, хотя есть и более специальные приложения с расширенным математическим функционалом. Используя Excel, посмотрим, как работает диаграмма на конкретном примере, Excel знает Диаграмму рассеяния, как точечную диаграмму.
Приступим. Нам нужно лучше понять связь между применением определенного оборудования и количеством дефектной продукции. Возьмем число употреблений инструмента, который нас интересует за десять разных дней и измеренную численность бракованной продукции за те же дни.
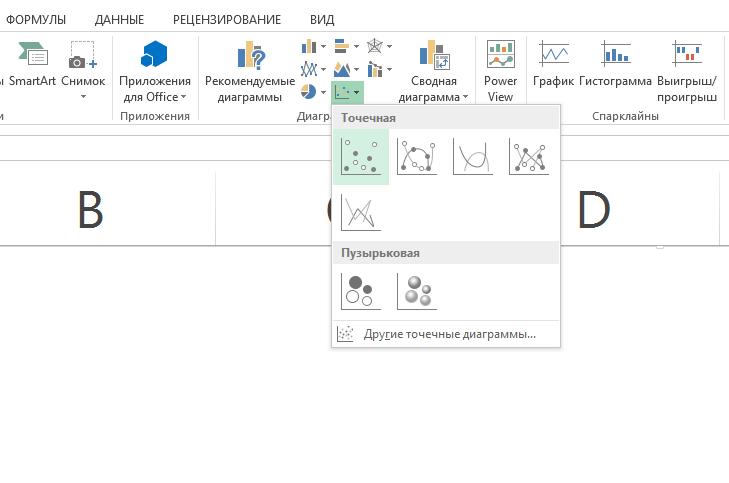
Теперь, когда у нас есть все необходимые исходные данные, выделим оба столбца левой кнопкой мыши и выберем в меню точечную диаграмму. В зависимости от версии программы у вас между осями координат могут появиться не все точки, а только точки одного ряда. В свойствах диаграммы или в меню к ней будет функция – добавить ряд. Ей-то и нужно воспользоваться, чтобы на графике появились оба типа данных.
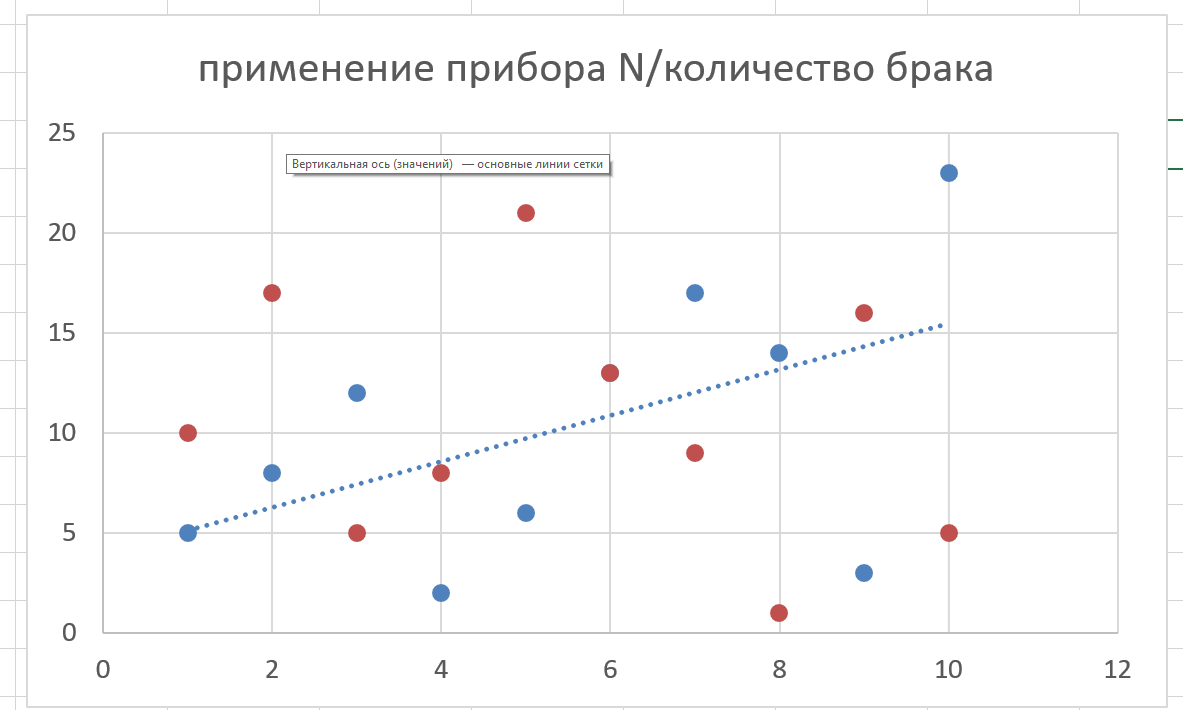
В меню диаграммы нужно также выбрать функцию добавления «линии тренда». Линия тренда – это геометрическое отображение средних значений анализируемых показателей.
Благодаря линии тренда мы и получаем возможность ответить на вопрос о том, есть ли связь между использованием нашего инструмента и количеством брака. Если все точки на графике веретенообразно сконцентрировались поблизости от линии тренда, то корреляция есть. Если же они более или менее рассредоточены, как в случае с нашей диаграммой, то никакой связи нет или она очень незначительна.
Даже во многих западных компаниях ручной документооборот с данными по качеству подчас превышает электронный. Поэтому кому-то может быть интересно и то, как диаграмма рассеяния делается в ручную. Это немногим сложнее. При начале работы нужно иметь столбцы сопоставимых данных нескольких типов, которые вы собираетесь сравнивать. Посмотрите, какие значения в ваших рядах чисел являются минимальными и максимальными. Исходя из этого можно рисовать оси для будущей диаграммы. Если числа очень большие, то оси можно масштабировать. После этого на график просто наносятся все необходимые точки. Для расчета линии тренда в математике используется целый ряд формул, каждая из которых хороша под конкретную ситуацию, в которой вы находитесь.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
«Управление и Оптимизация Производственного Предприятия»
Назначение метода
Японский союз ученых и инженеров в 1979 г. включил диаграмму разброса в состав семи методов контроля качества.
Цель метода
Выяснение существования зависимости и выявление характера связи между двумя различными параметрами процесса.
Суть метода
При наличии корреляционной зависимости между двумя факторами значительно облегчается контроль процесса с технологической, временной и экономической точек зрения.
Диаграмма разброса в процессе контроля качества используется также для выявления причинно-следственных связей показателей качества и влияющих факторов.
План действий
Для выяснения влияния одной переменной на другую следует собрать необходимые данные и внести их в листок регистрации.
По полученным данным построить диаграмму разброса и провести анализ диаграммы. Иногда желательно получить количественную оценку тесноты или силы связи между случайными величинами.
Особенности метода
По полученным экспериментальным точкам могут быть определены и числовые характеристики связи между рассматриваемыми случайными величинами: коэффициент корреляции и коэффициенты регрессии.
Диаграммы разброса (рассеяния)
Правила построения диаграммы разброса
В этом случае при осуществлении контроля причинных факторов х (откликов) характеристика у (функция) будет оставаться стабильной.
Достоинства метода
Наглядность и простота оценки связей между двумя переменными.
Недостатки метода
К оценке диаграммы следует привлекать тех, кто владеет информацией о продукции, чтобы исключить неправильное использование этого инструмента.
Ожидаемый результат
Принятие решения о проведении необходимых мероприятий на основании анализа диаграммы разброса.
Диаграмма рассеивания (разброса)
При проведении анализа данных часто на практике необходимо оценить зависимости между парами соответствующих элементов, например, вариация размера отверстия в зависимости от скорости вращения сверла, скорость вращения токарного станка и размер детали. Для этого используют диаграммы рассеивания, позволяющие без математической обработки данных установить зависимости по графическому представлению. Таким образом, данный статистический инструмент может быть использован линейным персоналом и менеджментом.
Данная диаграмма позволяет установить зависимости для
Для понимания связи между выбранными параметрами необходимо построить диаграмму рассеивания и понять ситуацию в целом.
Построение диаграммы:
Пример:
При процессе выпуска литьевых поддонов багажника компания сталкивается с проблемой при литье под давлением. Было высказано предположение, что причина тонких стенок поддонов, приводящих для конечного клиента к быстрому истиранию и повреждению заключается в вариации давления сжатого воздуха, которое меняется каждый день.
Было принято решение провести анализ и установить наличие или отсутствие данной зависимости (Рис.1).
Собраны данные за один месяц. Технология литья непрерывная, без выходных 
Рис.1
Чтение диаграммы рассеивания
По диаграмме рассеивания можно судить о об общем распределении пар чисел. Для этого необходимо, во-первых, выяснить если ли далеко отстоящие точки – они являются выбросами. Если есть далеко отстоящие точки, то их надо исключить из корреляционного анализа, но пренебрегать ими нельзя. Стоит обратить на них внимание, так как причиной выброса могут не только неверно занесённые данные, но внутренние причины процесса, которые могут дать полезную информацию (Рис.2). 
Рис.2
Для изучения связи между x и y необходимо вычислить коэффициент корреляции r.

Число n – число пар данных
S(xy) – ковариация – мера линейной зависимости двух случайных величин.
r ∈ [-1;1]
Диаграмма рассеяния в EXCEL
history 25 ноября 2018 г.
Построим диаграмму рассеяния для различных видов взаимосвязей двух переменных. Сгенерируем различные варианты трендов: линейный, квадратичный и затухающий синусоидальный.
Диаграмма рассеяния ( scatter plot ) используется для отображения возможной взаимосвязи между двумя переменными. Диаграмма рассеяния незаменима при проведении корреляционного и регрессионного анализа.
Возьмем 2 переменные Х и Y и, соответственно, выборку состоящую из нескольких пар значений (Х i ; Y i ). Для наглядности зададим различные типы зависимости между переменными: линейную, квадратичную и затухающую синусоидальную. Для этого сгенерируем соответствующие тренды и настроим случайный разброс переменной Y (по нормальному закону ).
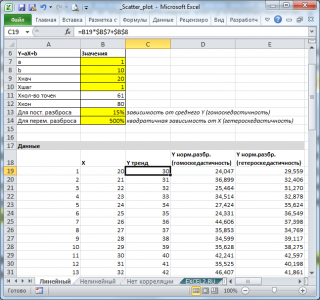
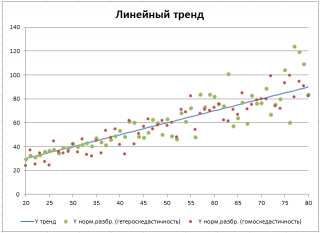
Сначала рассмотрим линейный тренд Y = aX + b (см. Файл примера, лист Линейный ). Параметры тренда (прямой линии) a и b зададим в отдельной табличке, там же зададим параметры отвечающие за величину дисперсии переменной Y.
Отображение информации о 3-х переменных на двухмерной диаграмме
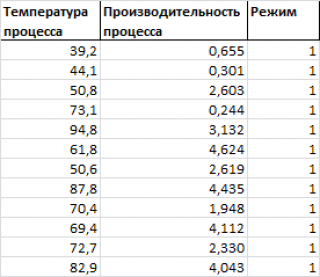
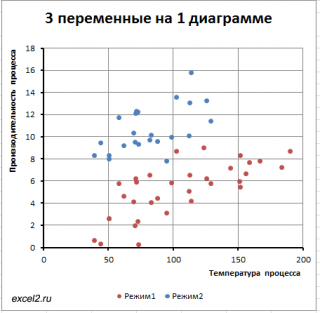
Предположим, что у нас имеются результаты измерения производительности некого непрерывного производственного процесса. Измерения проводились при различных рабочих температурах протекания процесса и в двух режимах.
Обратим внимание, что третья переменная Режим является категориальной (принимает только значения из ограниченного набора значений). В нашем случае переменная Режим принимает 2 значения: Режим №1 и Режим №2 (значения 1 и 2 присвоены номинально).
Пары значений ( производительность; температура ), относящиеся к Режиму №1 будем на диаграмме рассеяния выводить красным цветом, а относящиеся к Режиму №2 будем выводить синим ( файл примера лист 3-переменных ).
Категоризованные диаграммы
Если третья переменная – непрерывная величина, то для отображения данных можно использовать так называемые категоризованные диаграммы (coplot = conditioning plot).
Если пороговых значений 2, то понадобится 3 диаграммы и т.д. Эти диаграммы строятся аналогично диаграммам из предыдущего раздела.
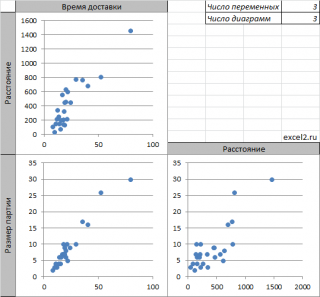
Матрица диаграмм рассеивания
Примечание : Чтобы найти количество диаграмм рассеяния в матрице, необходимо вычислить число сочетаний из n по 2, где n – число переменных. Например, для 4-х переменных число диаграмм равно ЧИСЛКОМБ(4;2) =6.
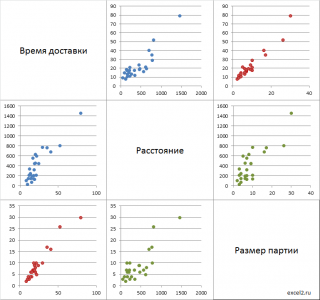
Примечание : Чтобы найти количество диаграмм рассеяния в такой (полной) матрице, необходимо вычислить число перестановок из n по 2, где n – число переменных. Например, для 4-х переменных число диаграмм равно ПЕРЕСТ(4;2) =12.