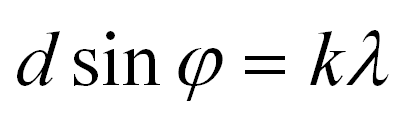Дифракция что это простыми словами

Дифракция и дисперсия света. Не путать!

Дисперсия света

Свет – электромагнитная волна. Видимый свет – это волны, имеющие длину в интервале от 380 до 770 нанометров.

Так вот, еще старина Ньютон заметил, что показатель преломления зависит от длины волны. Другими словами, красный свет, падая на поверхность и преломляясь, отклонится на другой угол, нежели желтый, зеленый и так далее. Эта зависимость и называется дисперсией.

Пропуская белый свет через призму, можно получить спектр, состоящий из всех цветов радуги. Это явление напрямую объясняется дисперсией света. Раз показатель преломления зависит от длины волны, значит, он зависит и от частоты. Соответственно, скорость света для разных длин волн в веществе также будет различна

Дисперсия света – зависимость скорости света в веществе от частоты.

Где применяется дисперсия света? Да повсюду! Это не только красивое слово, но и красивое явление. Дисперсия света в быту, природе, технике и искусстве. Вот, например, дисперсия красуется на обложке альбома группы Pink Floyd.

Дифракция света

Интерференция света – это когда две когерентные световые волны при наложении усиливают друг друга или наоборот ослабляют.

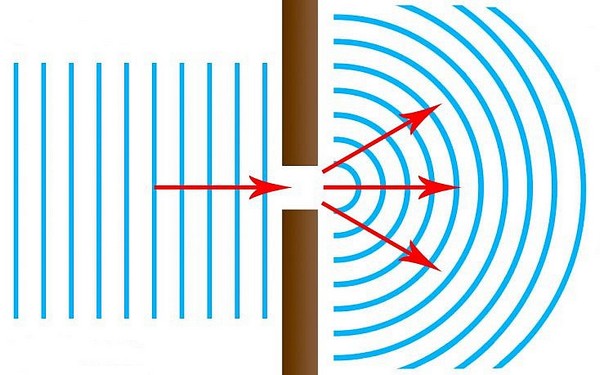
Дифракцией света называется явление отклонения света от прямолинейного направления при прохождении вблизи преграды.

Дифракция проявляется не только для света, но и для других волн. Например, для звуковых. Или для волн на море. Отличный пример дифракции – это то, как мы слышим песню группы Пинк Флойд из проезжающей мимо машины, когда сами стоим за углом. Если бы звуковая волна распространялась прямо, она бы просто не достигла наших ушей, и мы бы стояли в полной тишине. Согласитесь, скучно. Зато с дифракцией гораздо веселее.

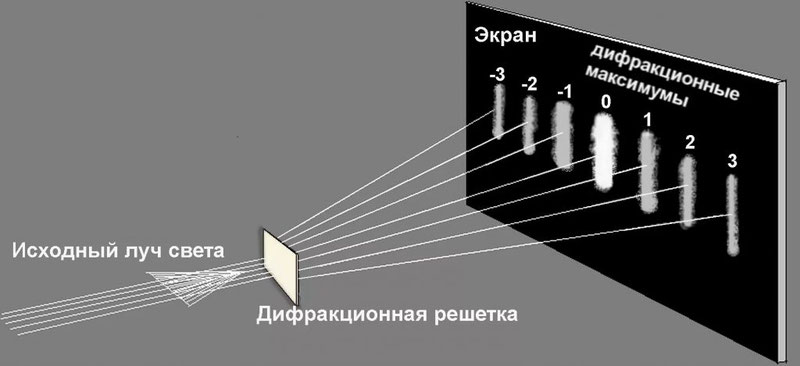
Для наблюдения явления дифракции используется специальный прибор – дифракционная решетка. Дифракционная решетка представляет собой систему препятствий, которые по размеру сопоставимы с длиной волны. Это специальные параллельные штрихи, выгравированные на поверхности металлической или стеклянной пластины. Расстояние между краями соседних щелей решетки называется периодом решетки или ее постоянной.

Что происходит со светом при прохождении дифракционной решетки? Попадая на решетку и встречая препятствие, световая волна проходит через систему прозрачных и непрозрачных областей, в результате чего разбивается на отдельные пучки когерентного света, которые после дифракции интерферируют друг с другом. Каждая длина волны отклоняется при этом на определенный угол, и происходит разложение света в спектр. В результате мы наблюдаем дифракцию света на решетке

Формула дифракционной решетки:

Здесь d – период решетки, фи – угол отклонения света после прохождения решетки, k – порядок дифракционного максимума, лямбда – длина волны.

Сегодня мы узнали, в чем чем заключается явления дифракции и дисперсии света. В курсе оптики очень сильно распространены задачи по теме интерференция, дисперсия и дифракция света. Авторы учебников очень любят подобные задачи. Чего нельзя сказать о тех, кому приходится их решать. Если Вы хотите легко справиться с заданиями, разобраться в теме, а заодно и сэкономить время, обратитесь к нашим авторам. Они помогут Вам справиться с любой задачей!

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Дифракция

Дифра́кция во́лн (лат. diffractus — буквально разломанный, переломанный, огибание препятствия волнами) — явление, которое проявляет себя как отклонение от законов геометрической оптики при распространении волн. Она представляет собой универсальное волновое явление и характеризуется одними и теми же законами при наблюдении волновых полей разной природы.

Дифракция неразрывно связана с явлением интерференции. Более того, само явление дифракции зачастую трактуют как случай интерференции ограниченных в пространстве волн (интерференция вторичных волн). Общим свойством всех эффектов дифракции является зависимость степени её проявления от соотношения между длиной волны и характерным размером неоднородностей среды , либо неоднородностей структуры самой волны. Наиболее заметно они проявляются при размерах неоднородностей, сравнимых с длиной волны. При размерах неоднородностей, существенно превышающих длину волны (на 3—4 порядка и более), явлением дифракции, как правило, можно пренебречь. В последнем случае распространение волн с высокой степенью точности описывается законами геометрической оптики. С другой стороны, если размер неоднородностей среды много меньше длины волны, то в таком случае дифракции проявляет себя в виде эффекта рассеяния волн. [1]

Изначально явление дифракции трактовалось как огибание волной препятствия, то есть проникновение волны в область геометрической тени. С точки зрения современной науки определение дифракции как огибания светом препятствия признается недостаточным (слишком узким) и не вполне адекватным. Так, с дифракцией связывают весьма широкий круг явлений, возникающих при распространении волн (в случае учёта их пространственного ограничения) в неоднородных средах.

Дифракция волн может проявляться:

Наиболее хорошо изучена дифракция электромагнитных (в частности, оптических) и акустических волн, а также гравитационно-капиллярных волн (волны на поверхности жидкости).

Содержание

Тонкости в толковании термина «дифракция»

В явлении дифракции важную роль играют исходные размеры области волнового поля и исходная структура волнового поля, которая подвержена существенной трансформации в случае, если элементы структуры волнового поля сравнимы с длиной волны или меньше её.

Например, ограниченный в пространстве волновой пучок имеет свойство «расходиться» («расплываться») в пространстве по мере распространения даже в однородной среде. Данное явление не описывается законами геометрической оптики и относится к дифракционным явлениям (дифракционная расходимость, дифракционное расплывание волнового пучка).

Исходное ограничение волнового поля в пространстве и его определённая структура могут возникнуть не только за счёт присутствия поглощающих или отражающих элементов, но и, например, при порождении (генерации, излучении) данного волнового поля.

Следует заметить, что в средах, в которых скорость волны плавно (по сравнению с длиной волны) меняется от точки к точке, распространение волнового пучка является криволинейным (см. градиентная оптика, градиентные волноводы, мираж). При этом волна также может огибать препятствие. Однако такое криволинейное распространение волны может быть описано с помощью уравнений геометрической оптики, и это явление не относится к дифракции.

Вместе с тем, во многих случаях дифракция может быть и не связана с огибанием препятствия (но всегда обусловлена его наличием). Такова, например, дифракция на непоглощающих (прозрачных), так называемых фазовых, структурах.

Поскольку, с одной стороны, явление дифракции света оказалось невозможным объяснить с точки зрения лучевой модели, то есть с точки зрения геометрической оптики, а с другой стороны, дифракция получила исчерпывающее объяснение в рамках волновой теории, то наблюдается тенденция понимать её проявление как любое отступление от законов геометрической оптики.

При этом следует заметить, что некоторые волновые явления не описываются законами геометрической оптики и, в то же время, не относятся к дифракции. К таким типично волновым явлениям относится, например, вращение плоскости поляризации световой волны в оптически активной среде, которое дифракцией не является.

Вместе с тем, единственным результатом так называемой коллинеарной дифракции с преобразованием оптических мод может быть именно поворот плоскости поляризации, в то время как дифрагированный волновой пучок сохраняет исходное направление распространения. Такой тип дифракции может быть реализован, например, как дифракция света на ультразвуке в двулучепреломляющих кристаллах, при которой волновые векторы оптической и акустической волн параллельны друг другу.

Ещё один пример: с точки зрения геометрической оптики невозможно объяснить явления, имеющие место в так называемых связанных волноводах, хотя эти явления также не относят к дифракции (волновые явления, связанные с «вытекающими» полями).

Раздел оптики «Оптика кристаллов», имеющей дело с оптической анизотропией среды, также имеет лишь косвенное отношение к проблеме дифракции. В то же самое время он нуждается в корректировке используемых представлений геометрической оптики. Это связано с различием в понятии луча (как направления распространения света) и распространения волнового фронта (то есть направления нормали к нему)

Отступление от прямолинейности распространения света наблюдается также в сильных полях тяготения. Экспериментально подтверждено, что свет, проходящий вблизи массивного объекта, например, вблизи звезды, отклоняется в её поле тяготения в сторону звезды. Таким образом, и в данном случае можно говорить об «огибании» световой волной препятствия. Однако, это явление также не относится к дифракции.

Частные случаи дифракции

Дифракция на щели

В качестве примера рассмотрим дифракционную картину возникающую при прохождении света через щель в непрозрачном экране. Мы найдём интенсивность света в зависимости от угла в этом случае. Для написания исходного уравнения используем принцип Гюйгенса.

Рассмотрим монохроматическую плоскую волну с амплитудой с длиной волны λ, падающую на экран с щелью ширины a.

Будем считать, что щель находится в плоскости x′-y′ с центром в начале координат. Тогда может предполагаться, что дифракция производит волну ψ, которая расходится радиально. Вдали от разреза можно записать

пусть (x′,y′,0) — точка внутри разреза, по которому мы интегрируем. Мы хотим узнать интенсивность в точке (x,0,z). Щель имеет конечный размер в x направлении (от до ), и бесконечна в y направлении ([, ]).

Расстояние r от щели определяется как:

Предполагая случай дифракции Фраунгофера, получим условие . Другими словами, расстояние до точки наблюдения много больше характерного размера щели (ширины). Используя биноминальное разложение и пренебрегая слагаемыми второго и выше порядков малости, можно записать расстояние в виде:

Видно, что 1/r перед уравнением не осциллирует, то есть даёт малый вклад в интенсивность по сравнению с экспоненциальным множителем. И тогда его можно записать приближённо как z.

Здесь мы введём некую константу ‘C’, которой обозначим все постоянные множители в предыдущем уравнении. Она, в общем случае может быть комплексной, но это не важно, так как в конце нас будет интересовать только интенсивность, и нам будет интересен только квадрат модуля.

В случае дифракции Фраунгофера мало, поэтому . такое же приближение верно и для . Таким образом, считая , приводит к выражению:

Используя формулу Эйлера и её производную: и .

где ненормированная синкус функция определена как .

Подставляя в последнее выражение для амплитуды, можно получить ответ для интенсивности в виде волны в зависимости от угла θ:

Источник

Дифракция света и дифракционная решетка

Содержание:

Первые опыты и активные исследования природы света начались еще в далеком XVII веке, когда итальянский ученый Франческо Гримальди впервые открыл такое интересное физическое явление как дифракция света. Что же такое дифракция света? Это отклонение света от прямолинейного распространения в силу определенных препятствий на его пути. Более научное объяснение причинам дифракции света было дано в начале XIX века английским ученым Томасом Юнгом, согласно нему дифракция света возможна благодаря тому, что свет представляет собой волну, идущую от своего источника и естественным образом искривляющуюся при попадании на определенные препятствия. Им же была изобретена первая дифракционная решетка, представляющая собой оптический прибор, работающий на основе дифракции света, то есть специально искривляющий световую волну.

Дифракция и интерференция света

Изучая поведение монохроматического пучка света, Томас Юнг, разделив его пополам, получил дифракционную картину, которая представляла собой последовательное чередование ярких и темных полос на экране. Волновая теория природы света, сформированная Юнгом, прекрасно объясняла это явление. Будучи волной, пучок света при попадании на непрозрачное препятствие искривляется, меняет траекторию своего движения. Так появляется дифракция света, при которой свет может, как целиком огибать препятствия (если длина световой волны больше размеров препятствия) или искривлять свою траекторию (когда размеры препятствий сопоставимы с длиной световой волны). Примером тут может быть попадание света через узкие щели или небольшие отверстия, как на фото ниже.

Луч света в пещере, наглядная иллюстрация дифракции света в природе.

А тут на картинке показано более схематическое изображение дифракции.

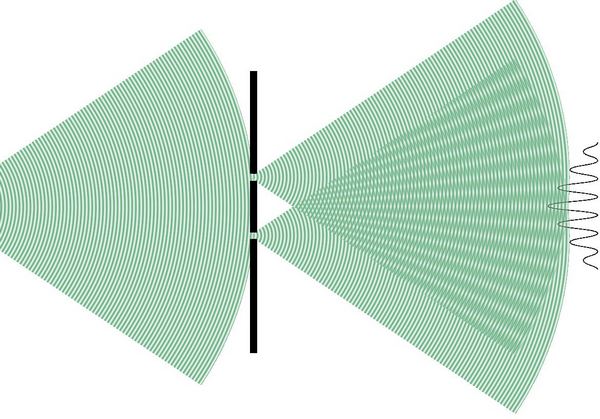
Физическое явление дифракции света дополняет еще одно важное свойство световой волны – интерференция света. Суть интерференции света заключается в накладывании одних световых волн на другие. В результате может происходить искривление синусоидальной формы результирующей волны.

Так схематически выглядит интерференция.

При этом, волны, которые накладываются, могут, как усиливать мощь общей световой волны (при совпадении амплитуд), так и наоборот погасить ее.

Дифракционная решетка

Как мы писали выше, дифракционная решетка представляет собой простой оптический прибор, который искривляет световую волну.

Вот так она выглядит.

Или еще чуть более маленький экземпляр.

Также дифракционную решетку можно охарактеризовать тремя параметрами:

Виды решеток

На самом деле есть целых два вида дифракционных решеток: прозрачная и отражающая.

Прозрачная решетка представляет собой прозрачную тонкую пластину из стекла или прозрачного пластика, на которую нанесены штрихи. Штрихи эти как раз и являются препятствиями для световой волны, сквозь них она не может пройти. Ширина штриха – это и есть, по сути, период дифракционной решетки d. А оставшиеся между штрихами прозрачные зазоры – это щели. Такие решетки наиболее часто применяются при выполнении лабораторных работ.

Отражающая дифракционная решетка – это металлическая либо пластиковая и отполированная пластина. Вместо штрихов на нее нанесены бороздки определенной глубины. Период d соответственно это расстояние между этими бороздками. Простым примером отражающей дифракционной решетки может быть оптический CD диск.

Такие решетки часто используют при анализе спектров излучения, так как благодаря их дизайну можно удобно распределить интенсивность максимумов дифракционной картины на пользу максимумов более высокого порядка.

Принцип работы

Представим, что на нашу решетку падает свет, имеющий плоский фронт. Это важный момент, так как классическая формула будет верна при условии, что волновой фронт является плоским и параллельным самой пластинке. Штрихи решетки будут вносить в этот световой фронт возмущение и как результат на выходе из решетки создаться ситуация будто бы работает множество когерентных (синхронных) источников излучения. Эти источники и являются причиной дифракции.

От каждого источника (по сути щели между штрихами решетки) будут распространяться световые волны, которые будут когерентными (синхронными) друг другу. Если на некотором расстоянии от решетки поместить экран, то мы сможем увидеть на нем яркие полосы, между которыми будет тень.

Формула

Яркие полосы, которые мы увидим на экране можно также назвать максимумами решетки. Если рассматривать условия усиления световых волн, то можно вывести формулу максимума дифракционной решетки, вот она.

Где θ_m это углы между перпендикуляром к центру пластинки и направлением на соответствующую линию максимума на экране. Величина m называется порядком дифракционной решетки. Она принимает целые значения и ноль, то есть m = 0, ±1, 2, 3 и так далее. λ – длина световой волны, а d – период решетки.

Таким образом, можно рассчитать положение всех максимумов решетки.

Разрешающая способность

Разрешающей способностью называют способность решетки разделить две волны с близкими значениями длины λ на два отдельных максимума на экране.

Применение

Какое же практическое применение дифракционной решетки, в чем ее конкретная польза? Дифракционная решетка является важным и незаменимым инструментов в спектроскопии, так с ее помощью можно узнать, например, химический состав далекой звезды. Свет, идущий от этой звезды, собирают зеркалами и направляют на решетку. Измеряя значения θ_m можно узнать все длины волн спектра, а значит и химические элементы, которые их излучают.

Видео

И в завершение интересное образовательное видео по теме нашей статьи от заслуженного учителя Украины – Павла Виктора, на наш взгляд его видео лекции на Ютубе по физике могут быть очень полезными для всех, кто изучает этот предмет.

Источник

Дифракция что это простыми словами

Часто волна встречает на своем пути небольшие (по сравнению с ее длиной) препятствия. Соотношение между длиной волны и размером препятствий определяет в основном поведение волны.

Волны способны огибать края препятствий. Когда размеры препятствий малы, волны, огибая края препятствий, смыкаются за ними. Так, морские волны свободно огибают выступающий из воды камень, если его размеры меньше длины волны или сравнимы с ней. За камнем волны распространяются так, как если бы его не было совсем (маленькие камни на рис. 127). Точно так же волна от брошенного в пруд камня огибает торчащий из воды прутик. Только за препятствием большого по сравнению с длиной волны размера (большой камень на рис. 127) образуется «тень»: волны за него не проникают.

Способностью огибать препятствия обладают и звуковые волны. Вы можете слышать сигнал машины за углом дома, когда самой машины не видно. В лесу деревья заслоняют ваших товарищей. Чтобы их не потерять, вы начинаете кричать. Звуковые волны в отличие от света свободно огибают стволы деревьев и доносят ваш голос до товарищей. Отклонение от прямолинейного распространения волн, огибание волнами препятствий, называется дифракцией. Дифракция присуща любому волновому процессу в той же мере, как и интерференция. При дифракции происходит искривление волновых поверхностей у краев препятствий.

Дифракция волн проявляется особенно отчетливо в случаях, когда размеры препятствий меньше длины волны или сравнимы с ней.

ДИФРАКЦИЯ СВЕТА

Если свет представляет собой волновой процесс, то, кроме интерференции, должна наблюдаться и дифракция света. Ведь дифракция — огибание волнами препятствий — присуща любому волновому движению. Но наблюдать дифракцию света нелегко. Дело в том, что волны заметным образом огибают препятствия, размеры которых сравнимы с длиной волны, а длина световой волны очень мала.

Пропуская тонкий пучок света через маленькое отверстие, можно наблюдать нарушение закона прямолинейного распространения света. Светлое пятно против отверстия будет большего размера, чем это следует ожидать при прямолинейном распространении света.

Опыт Юнга. В 1802 г. Юнг, открывший интерференцию света, поставил классический опыт по дифракции (рис. 203). В непрозрачной ширме он проколол булавкой два маленьких отверстия В и С на небольшом расстоянии друг от друга.

Эти отверстия освещались узким световым пучком, прошедшим в свою очередь через малое отверстие А в другой ширме. Именно эта деталь, до которой очень трудно было додуматься в то время, решила успех опыта. Интерферируют только когерентные волны. Возникшая в соответствии с принципом Гюйгенса сферическая волна от отверстия А возбуждала в отверстиях В и С когерентные колебания. Вследствие дифракции из отверстий В и С выходили два световых конуса, которые частично перекрывались. В результате интерференции световых волн на экране появлялись чередующиеся светлые и темные полосы. Закрывая одно из отверстий, Юнг обнаруживал, что интерференционные полосы исчезали. Именно с помощью этого опыта впервые Юнгом были измерены длины волн, соответствующие световым лучам разного цвета, причем весьма точно.

Теория Френеля. Исследование дифракции получило свое завершение в работах Френеля. Френель не только более детально исследовал различные случаи дифракции на опыте, но и построил количественную теорию дифракции, позволяющую в принципе рассчитать дифракционную картину, возникающую при огибании светом любых препятствий. Им же было впервые объяснено прямолинейное распространение света в однородной среде на основе волновой теории.

Этих успехов Френель добился, объединив принцип Гюйгенса с идеей интерференции вторичных волн. Об этом кратко уже упоминалось в четвертой главе.

Для того чтобы вычислить амплитуду световой волны в любой точке пространства, надо мысленно окружить источник света замкнутой поверхностью. Интерференция волн от вторичных источников, расположенных на этой поверхности, определяет амплитуду в рассматриваемой точке пространства.

Такого рода расчеты позволили понять, каким образом свет от точечного источника S, испускающего сферические волны, достигает произвольной точки пространства В (рис. 204).

Если рассмотреть вторичные источники на сферической волновой поверхности радиусе R. то результат интерференции вторичных волн от этих источников в точке В оказывается таким, как если бы лишь вторичные источники на малом сферическом сегменте ab посылали свет в точку В. Вторичные волны, испущенные источниками, расположенными на остальной части поверхности, гасят друг друга в(результате интерференции. Поэтому все происходит так, как если бы свет распространялся лишь вдоль прямой SB, т. е. прямолинейно.

Одновременно Френель рассмотрел количественно дифракцию на различного рода препятствиях.

Любопытный случай произошел на заседании Французской Академии наук в 1818 г. Один из ученых, присутствовавших на заседании, обратил внимание на то, что теории Френеля вытекают факты, явно противоречащие здравому смыслу. При определенных размерах отверстия и определенных расстояниях от отверстия до источника света и экрана в центре светлого пятна должно находиться темное пятнышко. За маленьким непрозрачным диском, наоборот, должно находиться светлое пятно в центре тени. Каково же было удивление ученых, когда поставленные эксперименты доказали, что так и есть на самом деле.

Дифракционные картины от различных препятствий. Из-за того, что длина световой волны очень мала, угол отклонения света от направления прямолинейного распространения невелик. Поэтому для отчетливого наблюдения дифракции (в частности, в тех случаях, о которых только что говорилось) расстояние между препятствием, которое огибается светом, и экраном должно быть велико.

На рисунке 205 показано, как выглядят на фотографиях дифракционные картины от различных препятствий: а) тонкой проволочки; б) круглого отверстия; в) круглого экрана.

Зоны Френеля для трехсантиметровой волны

Зонная пластинка для трехсантиметровых волн

Источник